Unit – 2
Stacks & Queue
Q1) What are the fundamental operations on stack?
A1) There are three fundamental operations on stack.
Push: Insert element to the stack
Pop: Delete element from stack
Peek: Returns element at the top of stack
We will see these operations with respect to an example.
Here we assume stack size is 3.
Initially the stack is empty. If a pop operation is called on an empty stack, then stack underflow occurs.
----- (empty stack)
Push element ‘7’ to the stack. Then stack becomes
| 7 | <-- top
-----
Push element ‘2’ to the stack. So new top of stack is 2.
| 2 | <-- top
| 7 |
-----
Push element ‘10’ to the stack. Now top of stack becomes 10.
|10 | <-- top
| 2 |
| 7 |
-----
Now the stack becomes full as we are assuming stack size is 3. If we insert one more element onto stack then stack overflow occurs.
Pop element from stack. Element 10 is popped out. Hence new top is 2.
| 2 | <-- top
| 7 |
-----
Since Stack is LIFO data structure element inserted most recently will be popped out first.
Pop element 2 from stack. Hence new top is 7.
| 7 | <-- top
-----
Pop element 7 from stack. Now stack becomes empty.
----- (empty stack)
Q2) What is the Array Implementation of Stack?
A2) Array implementation of stack is efficient if we know maximum size of stack.
Our stack must be able to store any type of data i.e.int, char, float or any other primitive data type.
Stack which is used to hold integer values must be able to hold float and character values.
For this we will not explicitly recode specific version of stack for each data type.
C++ provides this feature through class templates. Thus, we implement stack ADT in C++ using class templates.
When we create class template, it can perform operations on any type of data.
The compiler will automatically generate correct type of object, depending on the type we specify when object is created.
Thus, a stack ADT can be written as follows.
First, we create node structure template.
Template<class TYPE>
Struct Node
{
Type value;
};
Template<class TYPE> // class template
Class stack
{
Private:
Node<TYPE> *P; // pointer to structure
Int count; // total no. Of elements present in stack
Int max; // total no. Of elements allowed in stack
Int top; // index of top of stack
Public:
Stack(int size=100); // constructor to create a stack
~stack(); // destructor to destroy stack
Bool push(TYPE in); // function to insert element in stack
Bool pop(TYPE &out); // function to delete element in stack
Bool peek(TYPE& out); //return top element of stack
Bool isempty(); //check if stack is empty
Bool isfull(); //check if stack is full
Int stackcount();// returns no. Of elements currently in stack
};
Now we will see algorithms for these operations on stack in detail.
Create stack: stack()
Stack is created using constructor.
Steps
| Algorithm: stack(int size) | Description |
1 | Template<class TYPE> Stack<TYPE>::stack(int size) {
| Design constructor which takes stack size as an argument |
2 | Max=size;
| Assign size to max. Value of size can be passed or default size of 100 is assumed. |
3 | P=new Node<TYPE>[max]; | Allocate memory to P
|
4 | If(!P) { Cout<<”Memory overflow”; Abort(); }
| Check if memory is available. If memory is not available, abort and print “memory overflow “. |
5 | Count=0; Top=-1; }
| Initially stack is empty. So, count is 0 and stack top is -1.
|
2. Insert element in Stack: push()
Steps
| Algorithm: bool push(TYPE in)
| Description |
1 | Template<class TYPE> Bool stack<TYPE>::push(TYPE in) {
| Design function push which inserts element ‘in’ to stack |
2 | If(count>=max) Return false | Compare current total no. Of elements with maximum stack size. If stack is full then return false to indicate element cannot be inserted. |
3 | P[top].value=in
| If stack is not full copy data to top of stack
|
4 | Count++; Top++; Return true } | Increment count and top. Return true to indicate element is successfully inserted in stack. |
3. Remove element from stack: pop()
Steps
| Algorithm: bool pop(TYPE& out) | Description |
1 | Template<class TYPE> Bool stack<TYPE>::pop(TYPE& out) {
| Design function pop which deletes element on the top of stack. Out is a reference variable to receive element to be popped out. |
2 | Bool flag; If(count==0) Flag=false; | If stack is empty then set flag to false |
3 | Else { Out=P[top].value;
| If stack has elements, copy element at top of stack to variable out. |
4 | Top--; Count--; Flag=true; }
| Decrement count and top. Set flag to true to indicate pop is successful. |
5 | Return flag; } | Return flag |
4. Find top of stack(tos): peek
Steps
| Algorithm: bool peek(TYPE& out) | Description |
1 | Template<class TYPE> Bool stack<TYPE>::peek(TYPE& out) {
| Design function peek which returns element on the top of stack without modifying stack. Out is a reference variable to receive element at the top of stack. |
2 | Bool flag; If(count==0) Flag=false; | If stack is empty then set flag to false |
3 | Else { Out=P[top].value;
| If stack has elements, copy element at top of stack to variable out. |
4 | Flag=true; }
| Set flag to true. |
5 | Return flag; } | Return flag |
5. Check if the stack is empty: isEmpty()
Steps
| Algorithm: bool isEmpty() | Description |
1 | Template<class TYPE> Bool stack<TYPE>::isEmpty() {
| Design function isEmpty() which returns true if stack is empty and false otherwise. |
2 | Bool flag; If(count==0) Flag=true; | If stack is empty then set flag to true |
3 | Else Flag=false;
| If stack has elements set flag to false. |
4 | Return flag; } | Return flag |
6. Check if the stack is full: isFull()
Steps
| Algorithm: bool isFull() | Description |
1 | Template<class TYPE> Bool stack<TYPE>::isFull() {
| Design function isFull() which returns true if stack is full and false otherwise. |
2 | Bool flag; If(count==max) Flag=true; | Compare count with maximum number of elements allocated for a stack. If they are equal set flag to true. |
3 | Else Flag=false;
| If count is not equal to max set flag to false. |
4 | Return flag; } | Return flag |
7. Find total number of elements in stack: stackcount()
Steps
| Algorithm: int stackcount() | Description |
1 | Template<class TYPE> Int stack<TYPE>::stackcount() {
| Design function stackcount() which returns total number of elements present in stack. |
2 | Return count; } | ‘count’ specifies total number of elements present in stack so return count |
Destroy stack:~stack()
Stack is destroyed using destructor.
Steps
| Algorithm: ~stack() | Description |
1 | Template<class TYPE> Stack<TYPE>::~stack() {
| Design destructor to destroy stack |
2 | Delete[] P P=NULL; Count=0; Max=0; Top=-1; } | Release memory of P. Set variables count,max to 0 and top to -1. |
Program in C++ to perform various operations on stack.
#include<iostream.h>
# define int MAX 100
Template< class TYPE > //class template
Class Stack {
Int count; //number of elements present in stack
TYPE A[Max]; // Array of size MAX
TYPE out;
Int top; // index of top of stack
Public:
Stack(int MAX);
~Stack();
Bool push(TYPE);
TYPE pop();
Bool isEmpty();
Bool isFull();
Int stackcount();
Void display();
};
Template< class TYPE > //constructor to create stack
Stack< TYPE >::Stack(int MAX)
{
Count=0;
Top = -1;
}
Template< class TYPE > //destructor to remove stack
Stack< TYPE >::~Stack()
{ delete[] A;
Count=0;
MAX=0;
Top=-1;
}
Template< class TYPE>// function to push elements in stack
Void Stack< TYPE >::push(TYPE in)
{
If(count>=MAX)
Cout<<”stack overflow”
Count++;
Top++;
A[ top ] = in; //copy data to top of stack
}
Template< class TYPE > // Function to pop elements from stack
TYPE Stack< TYPE >::pop()
{ return A[ top-- ];
Count--;
}
Template< class TYPE> //Function to check if stack is full
Int Stack< TYPE>::isFull()
{
Return (count == Max);
}
Template< class TYPE> //Function to check if stack is empty
Int Stack< TYPE>::isEmpty()
{
Return (count == 0);
}
Template< class TYPE>
Int Stack< TYPE>::stackcount()
{
Return count;
}
Template< class TYPE> //Function to display stack elements
Void Stack<TYPE>::display()
{
If(top<0)
Cout<<”stack empty”;
For(int i=top;i>=0;i--)
Cout<<A[i]<<” ”;
}
Void main()
{
Int choice,data;
Stack<int> S; //create stack of integers
While(1)
{
Cout<<”Enter choice for operation”;
Cout<<”\t 1.PUSH”<<endl;
Cout<<”\t 2.POP”<<endl;
Cout<<”\t 3.ISFULL”<<endl;
Cout<<”\t 4.ISEMPTY”<<endl;
Cout<<”\t 5.Stackcount”<<endl;
Cout<<”\t 6.Display”<<endl;
Cin>>choice;
Switch(choice)
{
Case 1:
Cout<<”Enter element to be pushed”;
Cin>>data
S.push(data);
Break;
Case 2:
Out=S.pop();
Cout<<”Popped element is”<<out;
Break;
Case 3:
Int flag=S.isFull();
If(flag=1)
Cout<<”stack is full”;
Else
Cout<<”stack is not full”;
Break;
Case 4:
Int flag=S.isEmpty();
If(flag=1)
Cout<<”stack is empty”;
Else
Cout<<”stack is not empty”;
Break;
Case 5:int c=S.stackcount();
Cout<<”Stack count is”<<c;
Break;
Case 6: S.display();
Break;
} //end of switch
} //end of while
} //end of program
Q3) Explain the Expression Evaluation?
A3) An expression can be represented in one of the following forms.
Infix: Infix expression has operator between operands. E.g., A + B
Prefix: Prefix expression has operator before operands. E.g., + A B
Postfix: Postfix expression has operator after operands. E.g., A B +
Evaluation of an Infix Expression:
Infix expressions are always evaluated from left to right. While evaluating it we must take care of operator precedence.
Following table shows priority of operators in C++.


Priority of operators in C++
According to above table – and ! have highest priority and logical OR has least priority. If an expression consists of operators with same priority(*,/,%)then evaluation is performed from left to right. If expression consists of parentheses, then they are given top priority. Innermost parentheses are evaluated first.
E.g., Evaluate following infix expression
A / B – C + D * E. Given A=4, B=2, C=1, D=5, E=6
Considering above rules infix expression becomes.
((A / B) – C) + (D * E) Putting values in it
((4/2)-1) +(5*6)
(2-1) +(5*6)
1+30
31(Output)
Evaluation of prefix expression
Prefix expression has operator before operands. Prefix expression is always evaluated from right to left.
E.g., + 1 * 2 3
Evaluating from right to left, first operator we come across is ‘*’.so evaluate 2*3.so now expression becomes
+1 6
Again, start evaluating from right to left. Next operator is +.
Add 1 and 6. So final output is 7.
Evaluation of prefix expression using Stack
Steps for Evaluation of prefix expression using Stack are as follows.
Accept prefix expression from user
Scan the expression from right to left
If token is an operand, then push it in a stack.
If token is an operator, then pop corresponding operands and perform operation.
Push result in stack.
Move to next token
Repeat steps 3 to 6 till the end of prefix expression.
Q4) Solve this: -*+5 3 1 6?
A4)
Prefix Input |
Stack |
Operand 1 |
Operand 2 |
Output |
Description |
-* 5 3 + 1 6
|
| - | - | - | Initially stack is empty. Evaluate expression from right to left. |
-* 5 3 + 1
|
| - | - | - | First token is an operand hence push operand 6 in stack |
-* 5 3 +
|
| - | - | - | Next token is again operand hence push operand 1 in stack |
-* 5 3 |
|
1 |
6 |
7 |
Next token is operator +, hence pop 1 and 6 and perform addition. Result is 7. Push it in to stack
|
-* 5 |
| - | - | - | Next token is 3. Push it into stack.
|
-*
|
| - | - | - | Next token is 5. Push it into stack.
|
- |
| 5 | 3 | 15 | Next token is operator *, hence pop 5 and 3 and perform multiplication. Result is 15. Push it in to stack
|
|
| 15 | 7 | 8 | Next token is operator -, hence pop 15 and 7 and perform subtraction. Result is 8. Push it in to stack
|
Q5) Evaluate the following prefix expression using stack for A= 16, B= 2, C=3, D=10, and E=4. Prefix Expression is -+/A^BC*DE*AC
A5)
Prefix Input |
Stack |
Op 1 |
Op 2 |
Output |
Description |
-+/A^BC*DE*AC |
| - | - | - | Initially stack is empty. Evaluate expression from right to left. |
-+/A^BC*DE*A
|
| - | - | - | First token is an operand C hence push operand 3 in stack
|
-+/A^BC*DE* |
| - | - | - | Next token is an operand A hence push operand 16 in stack |
-+/A^BC*DE |
|
16 |
3 |
48 |
Next token is operator *, hence pop 3 and 16 and perform multiplication. Result is 48. Push it in to stack
|
-+/A^BC*D |
| - | - | - | Next token is E. Push it into stack.
|
-+/A^BC* |
| - | - | - | Next token is D. Push it into stack.
|
-+/A^BC |
| 10 | 4 | 40 | Next token is operator *, hence pop 4 and 10 and perform multiplication. Result is 40. Push it in to stack
|
-+/A^B |
| - | - | - |
Next token is C. Push it into stack
|
-+/A^ |
| - | - | - |
Next token is B. Push it into stack
|
-+/A
|
| 2 | 3 | 8 | Next token is operator ^, hence pop 2 and 3 and perform ^. Result is 8. Push it into stack.
|
-+/
|
| - | - | - | Next token is A. Push it into stack
|
-+ |
| 16 | 8 | 2 | Next token is operator /, hence pop 16 and 8 and perform /. Result of 16/8 is 2. Push it into stack.
|
- |
| 2 | 40 | 42 | Next token is operator +, hence pop 40 and 2 and perform +. Result of 40+2 is 42. Push it into stack. |
|
|
42 |
48 |
-6 |
Next token is operator -, hence pop 42 and 48 and perform -. Result of 42-48 is -6. Push it into stack. |
Hence final result is -6.
Evaluation of Postfix expression
Postfix expression has operator after operands. Postfix expression is evaluated from left to right.
Eg.6 4 2 * +
Evaluating from left to right first operator we come across is ‘*’.so evaluate 4*2.so now expression becomes
6 8 +. Again, start evaluating from left to right. Next operator is +. Add 6 and 8. So final output is 14.
Q6) Solve this 623+-382/+*2^3+?
A6)
Postfix Input
| Stack | Op1 | Op2 | Output | Description |
623+-382/+*2^3+
|
| - | - | - | Initially stack is empty. Evaluate expression from left to right. |
23+-382/+*2^3+
|
| - | - | - | First token is an operand 6. Push it into stack. |
3+-382/+*2^3+
|
| - | - | - | Next token is an operand 2. Push it into stack.
|
+-382/+*2^3+ |
| - | - | - | Next token is an operand 3. Push it into stack.
|
-382/+*2^3+
|
| 2 | 3 | 5 | Next token is operator +, hence pop 2 and 3 and perform +. Result of 2+3 is 5. Push it into stack. |
382/+*2^3+
|
| 6 | 5 | 1 | Next token is operator -, hence pop 5 and 6 and perform -. Result of 6-5 is 1. Push it into stack.
|
82/+*2^3+
|
| - | - | - | Next token is an operand 3. Push it into stack.
|
2/+*2^3+
|
| - | - | - | Next token is an operand 8. Push it into stack.
|
/+*2^3+
|
| - | - | - |
Next token is an operand 2. Push it into stack.
|
+*2^3+
|
| 8 | 2 | 4 | Next token is operator /, hence pop 2 and 8 and perform /. Result of 8/2 is 4. Push it into stack.
|
*2^3+
|
| 3 | 4 | 7 | Next token is operator +, hence pop 4 and 3 and perform +. Result of 3+4 is 7. Push it into stack.
|
2^3+
|
| 1 | 7 | 7 | Next token is operator *, hence pop 7 and 1 and perform *. Result of 1*7 is 7. Push it into stack.
|
^3+ |
| - | - | - | Next token is an operand 2. Push it into stack.
|
3+
|
| 7 | 2 | 49 | Next token is operator ^, hence pop 2 and 7 and perform ^. Result of 7^2 is 49. Push it into stack.
|
+ |
| - | - | - | Next token is an operand 3. Push it into stack.
|
|
|
49
|
3 |
52 | Next token is operator +, hence pop 3 and 49 and perform +. Result of 49+3 is 52. Push it into stack.
|
Hence final result is 52.
Eg.2: Evaluate the following postfix expression and show stack after every step in tabular form. Given A= 5, B= 6, C=2, D=12, and E=4.POSTfix Expression is
ABC+*DE\-
Postfix Input
| Stack | Op1 | Op2 | Output | Description |
ABC+*DE\- |
| - | - | - | Initially stack is Empty. Evaluate expression from left to right. |
BC+*DE\- |
| - | - | - | First token is an operand A i.e.,5. Push it into stack.
|
C+*DE\- |
| - | - | - | Next token is an operand B i.e.,6. Push it into stack.
|
+*DE\-
|
| - | - | - | Next token is an operand C i.e.,2. Push it into stack.
|
*DE\-
|
| 6 | 2 | 8 | Next token is operator +, hence pop 2 and 6 and perform +. Result of 6+2 is 8. Push it into stack.
|
DE\- |
| 5 | 8 | 40 | Next token is operator *, hence pop 8 and 5 and perform *. Result of 8*5 is 40. Push it into stack.
|
E\-
|
| - | - | - | Next token is an operand D i.e.,12. Push it into stack.
|
\-
|
| - | - | - | Next token is an operand E i.e.,4. Push it into stack.
|
- |
| 12 | 4 | 3 | Next token is operator \, hence pop 4 and 12 and perform \. Result of 12\4 is 3. Push it into stack.
|
|
| 40 | 3 | 37 | Next token is operator -, hence pop 3 and 40 and perform -. Result of 40-3 is 37. Push it into stack.
|
Hence final output is 37.
Q7) Define Expression conversion?
A7) Expression conversion is of following types
● Infix to Postfix
● Infix to Prefix
● Postfix to Infix
● Postfix to prefix
● Prefix to Infix
● Prefix to Postfix
● Infix to Postfix
Manual Transformation
Infix expression can be manually converted to postfix in following steps.
Fully parenthesize the infix expression considering operator precedence. There should be one set of parentheses for each operator.
Evaluate the innermost expression first. Replace right parenthesis with corresponding operator.
Remove left parentheses.
E.g., X+Y/Z
Step 1: (X+(Y/Z))
Step 2: (X+(YZ/)
(X (YZ/+
Step 3: XYZ/+
Stack Transformation
Infix expression can be converted to postfix using stack in following steps.
Initialize an empty stack.
While not to end of infix expression
Scan the expression from left to right.
Get the input token in the infix expression.
If the token is
A left parenthesis then push it onto the stack
A right parenthesis then Pop and display stack elements until a left parenthesis is encountered.
Note: Do not display parenthesis. Parenthesis has least priority in stack but highest priority when in input expression.
An operator: If the stack is empty or the input token has higher priority than the top stack, push onto the stack. Otherwise, pop and display the top stack element. Repeat the comparison of the input token with the new top stack element.
An operand: Just display it.
When the end of infix expression is reached, pop and display stack elements until the stack is empty.
Q8) Solve this: 4+5*9/1?
A8)
Infix | Stack | Postfix | Description |
4+5*9/1 |
|
| Initially stack is empty. Scan expression from left to right. |
+5*9/1 |
| 4
| First token is an operand 4 so add to postfix expression. |
5*9/1 |
| 4 | Next token is operator + and stack is empty so push it into stack |
*9/1
|
| 45 | Next token is an operand 5 so add to postfix expression.
|
9/1
|
| 45 | Next token is operator *. Compare * with +. * Has higher precedence over + so push it to stack. |
/1 |
| 459 | Next token is an operand 9 so add to postfix expression.
|
1 |
| 459* | Next token is operator /. Compare / with *. * Has higher precedence over / so pop it from stack and push /.
|
|
| 459*1 | Next token is an operand 1 so add to postfix expression. |
|
| 459*1/+ | Pop remaining tokens from stack and add to postfix expression |
Hence Postfix expression is 459*1/+
Q9) Convert (2+4) *(5-6)/ ((1-2) *(9+2)) to Postfix expression?
A9)
Infix | Stack | Postfix |
(2+4) *(5-6)/ ((1-2) *(9+2)) |
|
|
2+4) *(5-6)/ ((1-2) *(9+2)) | ( |
|
+4) *(5-6)/ ((1-2) *(9+2)) | ( | 2 |
) *(5-6)/ ((1-2) *(9+2)) | (+ | 24 |
*(5-6)/ ((1-2) *(9+2)) |
| 24+ |
(5-6)/ ((1-2) *(9+2)) | * | 24+ |
5-6)/ ((1-2) *(9+2)) | *( | 24+ |
-6)/ ((1-2) *(9+2)) | *( | 24+5 |
6)/ ((1-2) *(9+2)) | *(- | 24+5 |
)/ ((1-2) *(9+2)) | *(- | 24+56 |
/ ((1-2) *(9+2)) | * | 24+56- |
((1-2) *(9+2)) | / | 24+56-* |
(1-2) *(9+2)) | /( | 24+56-* |
1-2) *(9+2)) | /(( | 24+56-* |
-2) *(9+2)) | /(( | 24+56-*1 |
2)*(9+2)) | /((- | 24+56-*1 |
) *(9+2)) | /((- | 24+56-*12 |
*(9+2)) | /( | 24+56-*12- |
(9+2)) | /(* | 24+56-*12- |
9+2)) | /(*( | 24+56-*12- |
+2)) | /(*( | 24+56-*12-9 |
2)) | /(*(+ | 24+56-*12-9 |
)) | /(*(+ | 24+56-*12-92 |
) | /(* | 24+56-*12-92+ |
| / | 24+56-*12-92+* |
|
| 24+56-*12-92+*/ |
Q10) What are the Applications of stack?
A10) The following are the applications of the stack:
● Balancing of symbols: Stack is used for balancing a symbol. For example, we have the following program:
- Int main()
- {
- Cout<<"Hello";
- Coût<<"java point";
- }
As we know, each program has an opening and closing braces; when the opening braces come, we push the braces in a stack, and when the closing braces appear, we pop the opening braces from the stack. Therefore, the net value comes out to be zero. If any symbol is left in the stack, it means that some syntax occurs in a program.
● String reversal: Stack is also used for reversing a string. For example, we want to reverse a "java point" string, so we can achieve this with the help of a stack.
First, we push all the characters of the string in a stack until we reach the null character. After pushing all the characters, we start taking out the character one by one until we reach the bottom of the stack.
● UNDO/REDO: It can also be used for performing UNDO/REDO operations. For example, we have an editor in which we write 'a', then 'b', and then 'c'; therefore, the text written in an editor is abc. So, there are three states, a, ab, and abc, which are stored in a stack. There would be two stacks in which one stack shows UNDO state, and the other shows REDO state.
If we want to perform a UNDO operation, and want to achieve an 'ab' state, then we implement a pop operation.
● Recursion: The recursion means that the function is calling itself again. To maintain the previous states, the compiler creates a system stack in which all the previous records of the function are maintained.
● DFS (Depth First Search): This search is implemented on a Graph, and Graph uses the stack data structure.
● Backtracking: Suppose we have to create a path to solve a maze problem. If we are moving in a particular path, and we realize that we come on the wrong way. In order to come at the beginning of the path to create a new path, we have to use the stack data structure.
● Expression conversion: Stack can also be used for expression conversion. This is one of the most important applications of stack. The list of the expression conversion is given below:
● Infix to prefix
● Infix to postfix
● Prefix to infix
● Prefix to postfix
● Postfix to infix
● Memory management: The stack manages the memory. The memory is assigned in the contiguous memory blocks. The memory is known as stack memory as all the variables are assigned in a function called stack memory. The memory size assigned to the program is known to the compiler. When the function is created, all its variables are assigned in the stack memory. When the function completes its execution, all the variables assigned in the stack are released.
Q11) What is First-in-First out (FIFO) data structure?
A11) A Queue is a linear list in which data is inserted at one end called as rear and deleted from other end called as front. Queue removes elements in the same order in which they were inserted i.e., element inserted first is removed first. Hence, they are called First-in-First out (FIFO) data structure.
Q12) What is the Priority Queue?
A12) A priority queue is an ADT where every element has a "priority" associated with it. This priority determines the order in which they exit the queue. The elements with highest priority are removed before elements with low priority. If two elements have the same priority, they are removed according to their order in the queue.
Consider the scenario of jobs sent to a printer. These jobs are usually placed in a queue, so job that is submitted first will be printed first. But every time this is not feasible as some of the jobs are more important though they are submitted later. So, these important jobs should have precedence over other jobs which are submitted earlier. Such kind of application requires priority queue.
The common operations on priority queue are
- Insert: Insert’s element in priority queue. It is similar to enqueue operation of Queue.
- Delete: finds and removes the element from priority queue. It is similar to dequeue operation of Queue. The element removed is of highest priority.
Q13) Explain Array implementation of Priority Queue?
A13) All the functions are same as that of normal queue except dequeue as here element is deleted according to priority. We will look at dequeue function.
Let us assume array Q [] of size n.
TYPE dequeue ()
{
int max = 0;
// finding the index of the element with the highest priority
For (int i=0; i<n-1; i++)
{
if (Q[i] > Q[max])
{
max = i;
}
}
TYPE maxnum = Q[max];
Size--;
Q[max] = Queue[n];
Return maxnum;
Delete maxnum;
}
*******program for priority queue**********
#include<iostream>
#include<conio.h>
#include<process.h>
using namespace std;
template <class TYPE>
Struct Node //Node declaration
{
TYPE value; //data in a node
};
class Queue
{
Private:
Node<TYPE> * P; //
Int count;// number of elements present in queue
Int max; // maximum queue size
Int front; //index of element at front
Int rear // index of element at rear
Public:
Queue(int size=50)
{ max = x;
front=-1;
rear=-1;
Count=0
P = new TYPE[max];
}
~Queue();
Bool enqueue(TYPE in);
TYPE dequeue();
Bool isEmpty();
Bool isFull();
};
Template <class TYPE>
Bool Queue<TYPE>:: isEmpty()
{
return (count==0);
}
template <class TYPE>
bool Queue<TYPE>::isFull()
{
return (rear==(max-1));
}
template <class TYPE>
bool Queue<TYPE>:: enqueue(TYPE in)
{
if(isFull())
Return false;
Rear++;
P[rear].value=in;
return true;
If(count==0)
Front=0;
Count++;
Return true;
}
template <class TYPE>
TYPE Queue<TYPE>::deQueue()
{
if(isEmpty())
Cout<<”Queue is empty”;
Int m = 0;
// finding the index of the item with the highest priority
for (int i=0; i<max-1; i++)
{
if (P[i].value > P[m].value)
{
m = i;
}
}
TYPE maxnum = P[m];
count--;
P[m] = P[max];
Return maxnum;
Delete maxnum;
}
Template <class TYPE>
void Queue<TYPE>:: display()
{
for(int i=front;i<=rear;i++)
{
cout<<P[i]<<" <-- ";
}
cout<<endl;
}
}
void main(){
Queue<int> Q; //create queue of integers
int ch;
int x,flag;
do{
cout<<"\nEnter your choice:\n1.enqueue\n2.dequeue\n3.isfull\n4.isempty\5.display\n6.exit"<<endl;
cin>>ch;
switch(ch){
case 1:
Cout<<”Enter element to be inserted”;
Cin>>x;
flag=Q.enqueue(x)
If(flag==0)
cout<<"The queue is full"<<endl;
else
cout<<”element is inserted ";
break;
case 2:
TYPE T;
T=Q.dequeue();
cout<<”Deleted element is”<<T;
break;
Case 3:
Flag=Q.isFull();
If(flag==1)
cout<<Queue is full<<endl;
Else
Cout<<"queue is not full"<<endl;
Break;
Case 4:
Flag=Q.isEmpty();
If(flag==1)
cout<<Queue is empty<<endl;
Else
Cout<<"queue is not empty"<<endl;
Case 5:
Q.display();
break;
case 6:exit(1);
}
}while(ch);
getch();
}
Q14) Explain Operations on each Type of Queues?
A14) Queue operations may involve initializing or defining the queue, utilizing it, and then completely erasing it from the memory. Here we shall try to understand the basic operations associated with queues −
Enqueue () − add (store) an item to the queue.
Dequeue () − remove (access) an item from the queue.
Few more functions are required to make the above-mentioned queue operation efficient. These are −
Peek () − Gets the element at the front of the queue without removing it.
Isfull () − Checks if the queue is full.
Isempty () − Checks if the queue is empty.
In queue, we always dequeue (or access) data, pointed by front pointer and while enqueuing (or storing) data in the queue we take help of rear pointer.
Let's first learn about supportive functions of a queue −
Peek ()
This function helps to see the data at the front of the queue. The algorithm of peek () function is as follows −
Algorithm
Begin procedure peek
Return queue[front]
End procedure
Implementation of peek () function in C programming language −
Example
Int peek () {
Return queue[front];
}
Isfull ()
As we are using single dimension array to implement queue, we just check for the rear pointer to reach at MAXSIZE to determine that the queue is full. In case we maintain the queue in a circular linked-list, the algorithm will differ. Algorithm of isfull () function −
Algorithm
Begin procedure isfull
If rear equals to MAXSIZE
Return true
Else
Return false
Endif
End procedure
Implementation of isfull () function in C programming language −
Example
Bool isfull () {
If (rear == MAXSIZE - 1)
Return true;
Else
Return false;
}
Isempty ()
Algorithm of isempty () function −
Algorithm
Begin procedure isempty
If front is less than MIN OR front is greater than rear
Return true
Else
Return false
Endif
End procedure
If the value of front is less than MIN or 0, it tells that the queue is not yet initialized, hence empty.
Here's the C programming code −
Example
Bool isempty () {
If (front < 0 || front > rear)
Return true;
Else
Return false;
}
Q15) Define Enqueue Operation, with an Example?
A15) Queues maintain two data pointers, front and rear. Therefore, its operations are comparatively difficult to implement than that of stacks.
The following steps should be taken to enqueue (insert) data into a queue −
Step 1 − Check if the queue is full.
Step 2 − If the queue is full, produce overflow error and exit.
Step 3 − If the queue is not full, increment rear pointer to point the next empty space.
Step 4 − Add data element to the queue location, where the rear is pointing.
Step 5 − return success.
Insert Operation
Sometimes, we also check to see if a queue is initialized or not, to handle any unforeseen situations.
Algorithm for enqueue operation
Procedure enqueue(data)
If queue is full
Return overflow
Endif
Rear ← rear + 1
Queue[rear] ← data
Return true
End procedure
Implementation of enqueue () in C programming language −
Example
Int enqueue (int data)
If (isfull ())
Return 0;
Rear = rear + 1;
Queue[rear] = data;
Return 1;
End procedure
Q16) Define Dequeue Operation, with an example?
A16) Accessing data from the queue is a process of two tasks − access the data where front is pointing and remove the data after access. The following steps are taken to perform dequeue operation −
Step 1 − Check if the queue is empty.
Step 2 − If the queue is empty, produce underflow error and exit.
Step 3 − If the queue is not empty, access the data where front is pointing.
Step 4 − Increment front pointer to point to the next available data element.
Step 5 − Return success.
Remove Operation
Algorithm for dequeue operation
Procedure dequeue
If queue is empty
Return underflow
End if
Data = queue[front]
Front ← front + 1
Return true
End procedure
Implementation of dequeue () in C programming language −
Example
Int dequeue () {
If (isempty ())
Return 0;
Int data = queue[front];
Front = front + 1;
Return data;
}
Q17) Define stack?
A17) A Stack is a linear data structure that follows the LIFO (Last-In-First-Out) principle. Stack has one end, whereas the Queue has two ends (front and rear). It contains only one pointer (top pointer) pointing to the topmost element of the stack. Whenever an element is added in the stack, it is added on the top of the stack, and the element can be deleted only from the stack. In other words, a stack can be defined as a container in which insertion and deletion can be done from the one end known as the top of the stack.
Some key points related to stack
● It is called as stack because it behaves like a real-world stack, piles of books, etc.
● A Stack is an abstract data type with a predefined capacity, which means that it can store the elements of a limited size.
● It is a data structure that follows some order to insert and delete the elements, and that order can be LIFO or FILO.
Q18) What is a Circular Queue?
A18) A circular queue is similar to a linear queue as it is also based on the FIFO (First In First Out) principle except that the last position is connected to the first position in a circular queue that forms a circle. It is also known as a Ring Buffer.
Operations on Circular Queue
The following are the operations that can be performed on a circular queue:
● Front: It is used to get the front element from the Queue.
● Rear: It is used to get the rear element from the Queue.
● enQueue(value): This function is used to insert the new value in the Queue. The new element is always inserted from the rear end.
● deQueue(): This function deletes an element from the Queue. The deletion in a Queue always takes place from the front end.
Q19) Why was the concept of the circular queue introduced?
A19) There was one limitation in the array implementation of Queue. If the rear reaches to the end position of the Queue then there might be the possibility that some vacant spaces are left in the beginning which cannot be utilized. So, to overcome such limitations, the concept of the circular queue was introduced.
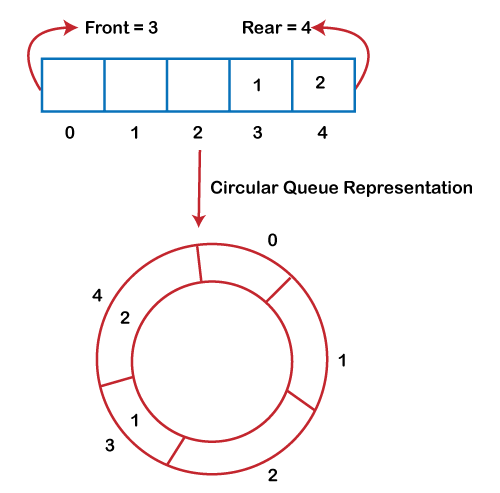
Fig: Circular queue
As we can see in the above image, the rear is at the last position of the Queue and the front is pointing somewhere rather than the 0th position. In the above array, there are only two elements and the other three positions are empty. The rear is at the last position of the Queue; if we try to insert the element then it will show that there are no empty spaces in the Queue. There is one solution to avoid such wastage of memory space by shifting both the elements at the left and adjust the front and rear end accordingly. It is not a practically good approach because shifting all the elements will consume lots of time. The efficient approach to avoid the wastage of the memory is to use the circular queue data structure.
Q20) Write applications of Circular Queue?
A20) The circular Queue can be used in the following scenarios:
● Memory management: The circular queue provides memory management. As we have already seen in the linear queue, the memory is not managed very efficiently. But in case of a circular queue, the memory is managed efficiently by placing the elements in a location which is unused.
● CPU Scheduling: The operating system also uses the circular queue to insert the processes and then execute them.
● Traffic system: In a computer-control traffic system, traffic lights are one of the best examples of the circular queue. Each traffic light gets ON one by one after every interval of time. Like red light gets ON for one minute then yellow light for one minute and then green light. After the green light, the red light gets ON.