Unit – 4

Trees

Q1) Define Tree Data Structure?

A1) A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.

Q2) Define Tree?

A2) A tree is defined as a set of one or more nodes T such that:

There is a specially designed node called root node

The remaining nodes are partitioned into N disjoint set of nodes T1, T2…. Tn, each of which is a tree.

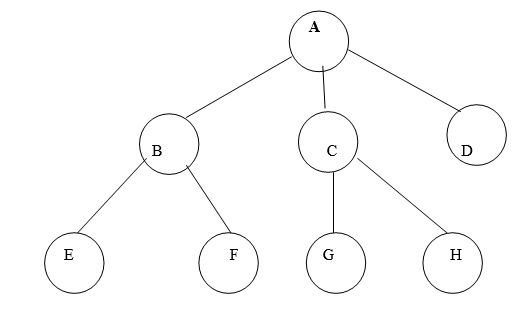
Fig.  Example of tree

In above tree A is Root.

Remaining nodes are partitioned into three disjoint sets:

{B, E, F}, {C, G, H}, {D}.

All these sets satisfy the properties of tree.

Some examples of TREE and NOT TREE

Each linear list is trivially a tree

Not a tree: cycle A→A

Not a tree: cycle B→C→E→D→B

Not a tree: two non- (connected parts, A→B and C→D→E

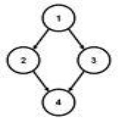
Fig. Examples of tree and no tree

Not a tree: undirected cycle 1-2-4-3

Q3) Write about Tree Terminologies?

A3) Tree Terminologies

1. Root – The top node in a tree.
2. Parent – The converse notion of child.
3. Siblings – Nodes with the same parent.
4. Descendant – a node reachable by repeated proceeding from parent to child.
5. Ancestor – a node reachable by repeated proceeding from child to parent.
6. Leaf – a node with no children. 
7. Internal node – a node with at least one child.
8. External node – a node with no children.
9. Degree – number of sub trees of a node.
10. Edge – connection between one node to another.
11. Path – a sequence of nodes and edges connecting a node with a descendant.
12. Level – The level of a node is defined by 1 + the number of connections between the node and the root.
13. Height of tree –The height of a tree is the number of edges on the longest downward path between the root and a leaf.
14. Height of node –The height of a node is the number of edges on the longest downward path between that node and a leaf.
15. Depth –The depth of a node is the number of edges from the node to the tree's root node.
16. Forest – A forest is a set of n ≥ 0 disjoint trees.

Q4) Define Binary tree? With example?

A4) A binary tree is a special case of tree in which no node of a tree can have degree more than two.

Definition of Binary Tree:

A binary tree is made of nodes, where each node contains a "left" pointer, a "right" pointer, and a data element. The "root" pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller "subtrees" on either side. A null pointer represents a binary tree with no elements -- the empty tree.

The formal recursive definition is A binary tree is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a binary tree.

Example of Binary Tree:

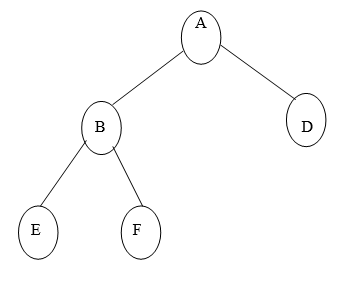
Q5) What are the types of Binary tree?

A5) There are two types of Binary Tree: -

●       Left Skewed Binary Tree.

●       Right Skewed Binary Tree.

1. Left Skewed Binary Tree:

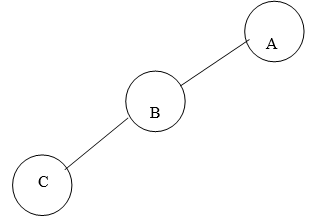
Fig.  Example of Left Skewed Binary Tree

In this tree, every node is having only Left sub tree.

2. Right Skewed Binary Tree: 

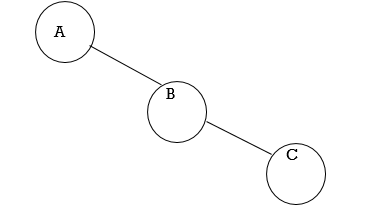
Fig. Example of Right Skewed Binary Tree

●       In this tree, every node has only the Right subtree.

Q6) Define Binary Search Tree?

A6) We now turn our attention to search tress: Binary Search tress in this chapter and AVL Trees in next chapter. As seen in previous chapter, the array structure provides a very efficient search algorithm, the binary search, but it is inefficient for insertion and deletion algorithms. On the other hand, linked list structure provides efficient insertion and deletion algorithms but it is very inefficient for search algorithm. So, what we need is a structure that provides efficient insertion, deletion as well as search algorithms.

Q7) What are the basic concepts of Binary Search Tree?

A7) A Binary Search Tree is a binary tree with the following properties:

1. It may be empty and every node has an identifier.

2. All nodes in left subtree are less than the root.

2. All nodes in right subtree are greater than the root.

4. Each subtree is itself a BST.

Q8) Define Threaded Binary Tree? In brief.

A8) Binary trees, including binary search trees and their variants, can be used to store a set of items in a particular order. For example, a binary search tree assumes data items are ordered and maintain this ordering as part of their insertion and deletion algorithms. One useful operation on such a tree is traversal: visiting the items in the order in which they are stored. A simple recursive traversal algorithm that visits each node of a BST is the following. Assume t is a pointer to a node, or NULL.

A threaded binary tree defined as follows:

"A binary tree is threaded by making all right child pointers that would normally be null point to the inorder successor of the node (if it exists), and all left child pointers that would normally be null point to the inorder predecessor of the node."

It is also possible to discover the parent of a node from a threaded binary tree, without explicit use of parent pointers or a stack. This can be useful where stack space is limited, or where a stack of parent pointers is unavailable (for finding the parent pointer via DFS).

Inorder Threaded Binary Tree:

In inorder threaded binary tree, left thread points to the predecessor and right thread points to the successor.

Types Inorder Threaded Binary Tree:

1. Right Inorder Threaded Binary Tree.

In this type of TBT, only right threads are shown which points to the successor.

2. Left Inorder Threaded Binary Tree.

In this type of TBT, only left threads are shown which points to the predecessor.

For TBT it is not necessary that the tree must be BST, it can be applied to general tree.

Q9) Draw inorder TBT for following data: 10, 8, 1 5, 7, 9, 12, 18?

A9) Inorder TBT

Step 1: The general for given data is:

Step 2: Write inorder sequence for the above tree:

7, 8, 9, 10, 12, 15, 18

Step 3: Make groups containing three nodes per group like:

Step 4: It means right thread of 7 point to 8 provided that 7 node is not having right link, means right link of 7 is NULL and thread is pointing in bottom-up direction and not in top to bottom.

Left thread of 7 and Right thread of 18 will point to head node.

Step 5: Draw TBT with right and left threads.

Head Node

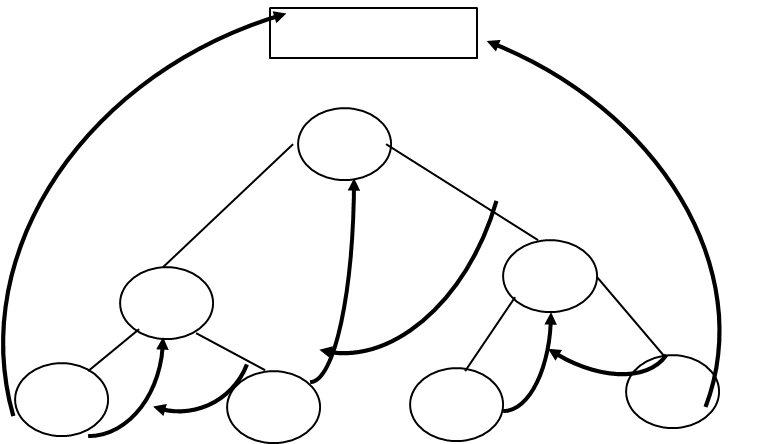
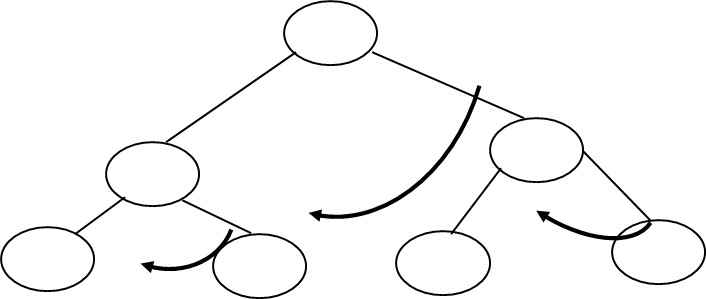
Left Inorder Threaded Binary Tree: 

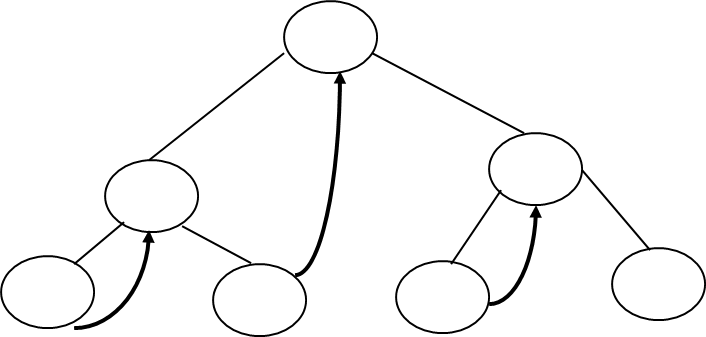
Right Inorder Threaded Binary Tree:

Q10) Define AVL trees? With example?

A10) The concept is developed by three persons: Adelsion, Velski and Landis.

Balance Factor:

Balance factor is (Height of left sub tree - Height of right sub tree)

Height Balance Tree:

An empty tree is height balanced. If T is non-empty binary tree with TL and TR as left and right sub tress, then T is height balanced if and only if:

TL and TR are height balanced.

HL- HR =1

HL and   HR are heights of left and right sub tree.

For ant node in AVL tree Balance factor must be -1 or 0 or 1.

Following rotations are performed on AVL tree if any of the nodes is unbalanced.

1. LL Rotation.

2. LR Rotation.

3. RL Rotation.

4. RR Rotation.

1. LL Rotation:

Count from unbalanced node. First left node becomes the root node.

2. LR Rotation:

Count from unbalanced node. Go for left node and then right node say X.  The node X becomes the root node.

3. RL Rotation:

Count from unbalanced node. Go for right node and then left node say X.  The node X becomes the root node.

4. RR Rotation:

Count from unbalanced node. First right node becomes the root node.

While inserting data in AVL tree, Follow the property of Binary search tree (left<root<right)

Q11) Obtain an AVL tree by inserting one integer at a time in the following sequence: 150,155,160,115,110,140,120,145,130?

A11) AVL tree

Step 1: insert 150

150

Balance factor for 150 is: 0 – 0=0

1500

NO ROTATION IS REQUIRED.

Step 2: insert 155

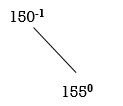
Balance factor for 150 is: 0 – 1= -1

Both nodes are balanced.

NO ROTATION IS REQUIRED.

STEP 3: INSERT 160.

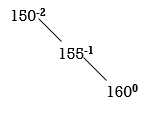
Balance factor of 150 is -2. So, 150 is unbalanced. Some rotation is required to do 150 as balanced node.  Start from 150 towards 160.

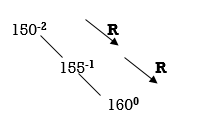
We get RR direction. So, we have to perform RR rotation.

In RR rotation, Count from unbalanced node. First right node becomes the root node. So here first R is 155. So, 155 will become the root.

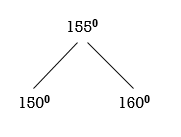
Now all nodes are balanced.

STEP 4: INSERT 115.

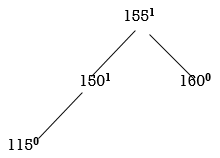
All nodes are balanced. NO ROTATION IS REQUIRED

STEP 5: INSERT 110

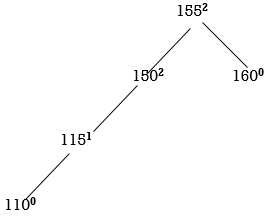
155 and 150 are unbalanced. Whenever two/more nodes are unbalanced, we have to consider the lowermost node first. i.e.,150. Move from 150 towards the node causing unbalancing (110)

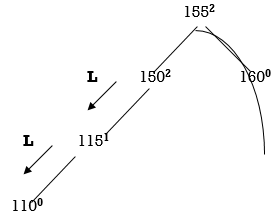
So, we have to perform LL Rotation. In LL rotation, Count from unbalanced node. First Left node becomes the root node. So here first L is 115. So, 115 will become the root.

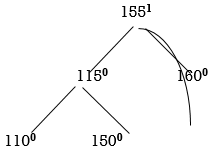
Now all nodes are balanced.

STEP 6: INSERT 140      

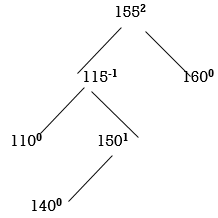
155 is unbalanced. Count moves from 155 towards the node causing unbalancing (140).

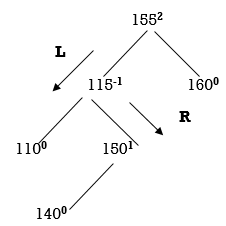
So, we have to perform LR Rotation. In LR rotation, Count from unbalanced node (155). Go for left node and then right node (150).  150 will become root node

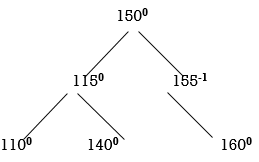
Now all nodes are balanced.

STEP 7: INSERT 120

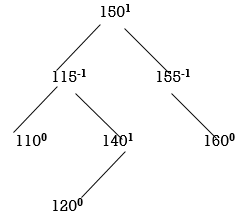
Now all nodes are balanced.

STEP 7: INSERT 145

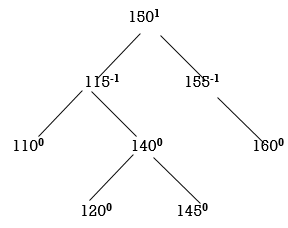
Now all nodes are balanced.

STEP 8: INSERT 130

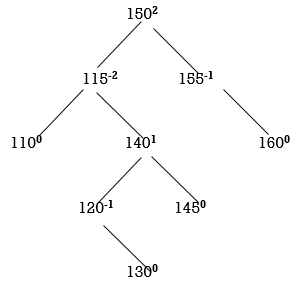
Two nodes 150 and 115 are unbalanced. First consider 115. Count moves from 115 towards the node causing unbalancing (130).

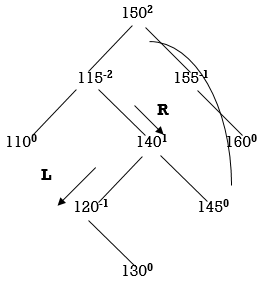
So, we have to perform RL Rotation. In RL rotation, Count from unbalanced node (115). Go for Right node and then Left node (120).  120 will become root node.

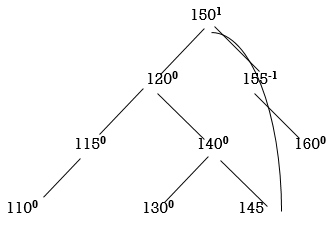
Now all nodes are balanced.

Thus, the tree is balanced.

Q12) What are the basic operation of a Tree?

A12) Following are the basic operations of a tree −

●       Search − Searches an element in a tree.

●       Insert − Inserts an element in a tree.

●       Pre-order Traversal − Traverses a tree in a pre-order manner.

●       In-order Traversal − Traverses a tree in an in-order manner.

●       Post-order Traversal − Traverses a tree in a post-order manner.

Q13) Explain Search Operation?

A13) Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.

Algorithm

Struct node* search(int data){

Struct node *current = root;

Printf("Visiting elements: ");

While(current->data != data){

If(current != NULL) {

Printf("%d ",current->data);

//go to left tree

If(current->data > data){

Current = current->leftChild;

}  //else go to right tree

Else {               

Current = current->rightChild;

}

//not found

If(current == NULL){

Return NULL;

}

}   

}

Return current;

}

Q14) Define Insert Operation?

A14) Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.

Algorithm

Struct node* search(int data){

Struct node *current = root;

Printf("Visiting elements: ");

While(current->data != data){

If(current != NULL) {

Printf("%d ",current->data);

//go to left tree

If(current->data > data){

Current = current->leftChild;

}  //else go to right tree

Else {               

Current = current->rightChild;

}

//not found

If(current == NULL){

Return NULL;

}

}   

}

Return current;

}

Q15) Define B-tree?

A15) Introduction to B-Trees

A B-tree is a tree data structure that keeps data sorted and allows searches, insertions, and deletions in logarithmic amortized time. Unlike self-balancing binary search trees, it is optimized for systems that read and write large blocks of data. It is most commonly used in database and file systems.

The B-Tree Rules

Important properties of a B-tree:

B-tree nodes have many more than two children.

A B-tree node may contain more than just a single element.

The set formulation of the B-tree rules: Every B-tree depends on a positive constant integer called MINIMUM, which is used to determine how many elements are held in a single node.

Rule 1: The root can have as few as one element (or even no elements if it also has no children); every other node has at least MINIMUM elements.

Rule 2: The maximum number of elements in a node is twice the value of MINIMUM.

Rule 3: The elements of each B-tree node are stored in a partially filled array, sorted from the smallest element (at index 0) to the largest element (at the final used position of the array).

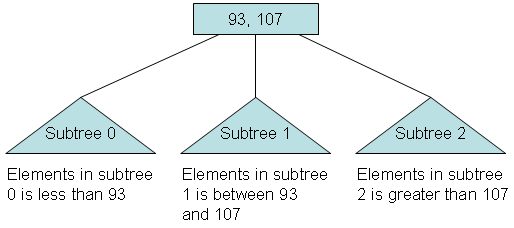
Rule 4: The number of subtrees below a nonleaf node is always one more than the number of elements in the node.

Subtree 0, subtree 1, ...

Rule 5: For any nonleaf node:

An element at index i is greater than all the elements in subtree number i of the node, and An element at index i is less than all the elements in subtree number i + 1 of the nodes.

Rule 6: Every leaf in a B-tree has the same depth. Thus, it ensures that a B-tree avoids the problem of an unbalanced tree.

Q16) Define B+ Tree?

A16) Most queries can be executed more quickly if the values are stored in order. But it's not practical to hope to store all the rows in the table one after another, in sorted order, because this requires rewriting the entire table with each insertion or deletion of a row.

This leads us to instead imagine storing our rows in a tree structure. Our first instinct would be a balanced binary search tree like a red-black tree, but this really doesn't make much sense for a database since it is stored on disk. You see, disks work by reading and writing whole blocks of data at once — typically 512 bytes or four kilobytes. A node of a binary search tree uses a small fraction of that, so it makes sense to look for a structure that fits more neatly into a disk block.

Hence the B+-tree, in which each node stores up to d references to children and up to d − 1 keys. Each reference is considered “between” two of the node's keys; it references the root of a subtree for which all values are between these two keys.

Here is a fairly small tree using 4 as our value for d.

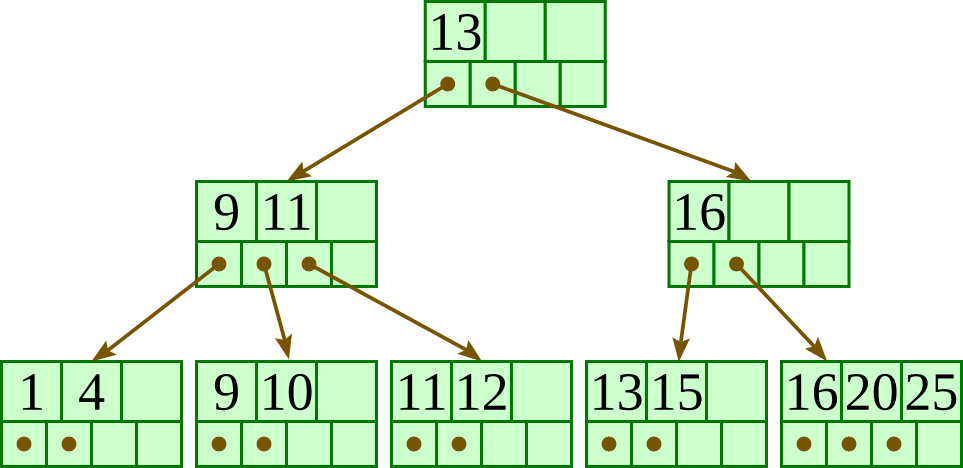
A B+-tree requires that each leaf be the same distance from the root, as in this picture, where searching for any of the 11 values (all listed on the bottom level) will involve loading three nodes from the disk (the root block, a second-level block, and a leaf).

In practice, d will be larger — as large, in fact, as it takes to fill a disk block. Suppose a block is 4KB, our keys are 4-byte integers, and each reference is a 6-byte file offset. Then we'd choose d to be the largest value so that 4 (d − 1) + 6 d ≤ 4096; solving this inequality for d, we end up with d ≤ 410, so we'd use 410 for d. As you can see, d can be large.

A B+-tree maintains the following invariants:

Every node has one more reference than it has keys.

All leaves are at the same distance from the root.

For every non-leaf node N with k being the number of keys in N: all keys in the first child's subtree are less than N's first key; and all keys in the ith child's subtree (2 ≤ i ≤ k) are between the (i − 1) th key of n and the ith key of n.

The root has at least two children.

Every non-leaf, non-root node has at least floor (d / 2) children.

Each leaf contains at least floor (d / 2) keys.

Every key from the table appears in a leaf, in left-to-right sorted order.

In our examples, we'll continue to use 4 for d. Looking at our invariants, this requires that each leaf have at least two keys, and each internal node to have at least two children (and thus at least one key).

Q17) Create a Binary Search Tree by adding the integers in the following order… 10,12,5,4,20,8,7,15 and 13?

A17) The following items are added into a Binary Search Tree in the following order.

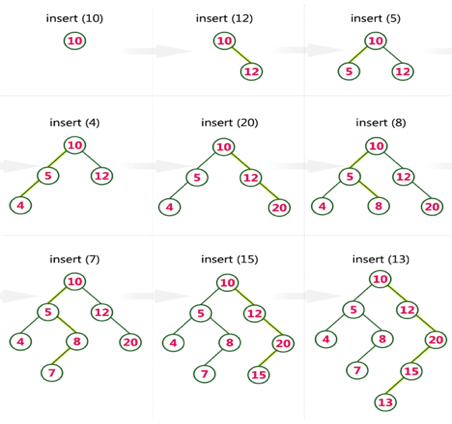
Q18) Write the difference between B tree and B+ tree?

A18) Difference between B tree and B+ tree

Q19) Write the difference between binary search tree and AVL tree?

A19) Difference between Binary search tree and AVL tree