Unit - 1
Set theory, relations and functions
Q1) What is the significance of discrete maths?
A1)
According to K.H Rosen, discreet mathematics has more than one purpose but more importantly it equips computer science students with logical and mathematical skills.
By B.Miller and D. Ranum, A computing machine end is to develop an algorithm, a measure by step list of instructions in work outing a job. Algorithm are finite procedures that if followed will work out the job.
Discreet mathematics is the study of mathematics which deals on discreet structures like graphs, trees and networks.
It deals with discreet objects like integers and rational numbers which are separated from each other
Discreet mathematics is the language of computer science
The field of mathematics that are considered to be part of discrete mathematics include graph theory and the theory of computation. Topics in number theory such as congruence’s and recurrence relations are also considered part of discrete mathematics.
Theoretical computer science includes areas of Theoretical computer science includes areas of discrete mathematics relevant to computing. It draws heavily on graph theory and logic. Included within theoretical computer science is the study of algorithms for computing mathematical results.
Q2) Define statement.
A2)
When a declarative sentence which is true or false but not both is called statement.
The truth values “true” and “false” of a statement are denoted by T ad F respectively. We can denote them by 0 and 1 as well.
Q3) What are the laws of formals?
A3)
Laws of formal-
1. Law of contradiction- According to the law of contradiction the same predicate cannot be both affirmed and denied precisely of the same subject
For every preposition p is not the same that p is both true and false.
2. Law of excluded middle- If p is a statement, then either p is true or p is false and there cannot be middle ground.
Q4) Define connectives and disjunctions.
A4)
Connectives-
Statements in mathematical logic are combinations of simpler statements joined by words and phrases like ‘and’. ‘or’, ‘if and only if’, etc. These words and phrases are called logical connectives.
Disjunction-
Definition: The disjunction of two propositions p and q is the compound statement 10 Elementary Logic p or q, denoted by p ∨ q.
For example, ‘Aman has a house or Amit has a house’ Is the disjunction of p and q, where-
p: Aman has a house, and
q: Amit has a house.
Q5) Obtain the truth value of the conjunction of ‘2 ÷5 = 1’ and ‘Ramesh is in Jaipur’.
A5)
Let p: 2 ÷5 = 1, and
q:Ramesh is in Jaipur.
Then the truth value of p is F. Therefore, from Table 3 you will find that the truth
Value of p ∧ q is F.
Q6) What is converse?
A6)
The converse of p → q is q → p. In this case we also say ‘p is necessary for q’, or ‘p if q’ when we combine an implication and its converse, then-
Let p and q be two propositions. The compound statement
(p→ q) ∧(q → p) is the bi-conditional of p and q. We denote it by p ↔ q, and
(Read) as ‘p if and only q’.
We use ‘if and only ‘if’ as iff
We also say that ‘p implies and is implied by q’. Or ‘p is necessary and sufficient
For q’.
Q7) What is compound proposition?
A7)
Many propositions are composite, that is, composed of sub-propositions and various connectives discussed
Subsequently such composite propositions are called compound Propositions. A proposition is said to be primitive if it cannot be broken down into simpler propositions, that is, if it is not composite.
Following two propositions are composite:
“Roses are red and violets are blue.” and “John is smart or he studies every night.”
Q8) What is the principal of inclusion and exclusion?
A8)
There is a formula for n(A ∪ B) even when they are not disjoint, called the Inclusion–Exclusion Principle
The Inclusion-Exclusion principle can be stated as below-
Let A and B any two finite sets, then-

Meaning- Here if we have to find the number  of elements in the union of A and B.
of elements in the union of A and B.
So then we add n(A) and n(B) which means we are including these two.
And then we exclude 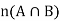 .
.
Q9) Suppose a list A contains the 30 students in a mathematics class, and a list B contains the 35 students in an English class, and suppose there are 20 names on both lists. Find the number of students) (a) only on list A, (b) only on list B, (c) on list A or B (or both), (d) on exactly one list.
A9)
(a) List A has 30 names and 20 are on list B; hence 30 − 20 = 10 names are only on list A.
(b) Similarly, 35 − 20 = 15 are only on list B.
(c) We seek n(A ∪ B). By inclusion–exclusion,
n(A ∪ B) = n(A) + n(B) − n(A ∩ B) = 30 + 35 − 20 = 45.
In other words, we combine the two lists and then cross out the 20 names which appear twice.
(d) By (a) and (b), 10 + 15 = 25 names are only on one list; that is, n(A ⊕ B) = 25.
Q10) Prove 1+2+...+n=n(n+1)/2 using a proof by induction.
A10)
Let n=1: 1 = 1(1+1)/2 = 1(2)/2 = 1 is true,
Step-1: Assume n=k holds: 1+2+...+k=k(k+1)/2
Show n=k+1 holds: 1+2+...+k+(k+1)=(k+1)((k+1)+1)/2
Substitute k with k+1 in the formula to get these lines. Notice that I write out what I want to prove.
Step-2: Now start with the left side of the equation
1+2+...+(k+1)=1+2+...+k+(k+1)
=k(k+1)/2 + (k+1)
=(k(k+1) + 2(k+1))/2 by 2/2=1 and distribution of division over addition
=(k+2)(k+1)/2 by distribution of multiplication over addition
=(k+1)(k+2)/2 by commutativity of multiplication.
Q11) What is ordered pair?
A11)
An ordered pair of element a and b, where a is designated as the first element and b as the second element, it is denoted by (a, b).
In particular
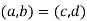
If and only if a = c and b = d. Thus
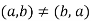
Unless a = b.
Q12) What is n-tuple?
A12)
A finite sequence over a set A is a function from {1, 2,….,n} into A, and it is usually denoted by
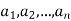
Such a sequence which is finite is called an n-tuple.
Here ‘n’ is a non-negative integer.
Tuples are written by listing the elements with parentheses ().
Q13) Define Cartesian product.
A13)
Suppose we have two sets A and B, then we can form the set-
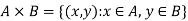
To be the set of all ordered pairs (x,y) where x is an element of A and y is an element of B.
Here we call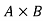 the Cartesian product of A and B.
the Cartesian product of A and B.
Q14) Define relation.
A14)
Let X and Y are two sets, A relation from X to Y is a subset of 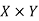 .
.
Now suppose R is a relation form X to Y, then R is a set of ordered pairs where each first element comes from X and each second element comes from Y.
For each pair 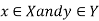 , one the following rule is true-
, one the following rule is true-
1. 
2.
The domain of a relation R is the set of all first elements of the ordered pairs which belongs to R, and range is the second element.
Q15) Let Z denote the set of integers and the relation R in Z be defined by “aRb” iffa – b is an even integer”. Then show that R is an equivalence relation.
A15)
1. R is reflexive; since
∅ = a −a is even, hence aRa for every a∈Z.
2. R is symmetric:
If a – b is even then b – a = – (a – b) is also even hence aRb⇒bRa
3. R is transitive: for if aRb and bRc then both a – b and b – c are even.
Consequently, a – c = (a – b) + (b – c) is also even.
∴aRb and bRc⇒aR c
Thus, R is an equivalence relation.
Q16) Define partial ordering and comparability.
A16)
Partial orderings-
A relation R on a set Sis called a partial order relation in Sif R is, Reflexive Anti-symmetric and transitive.
A set S together with a partial ordering R is called a partially ordered set.
We denote a partial order relation by the symbol ≤.
Comparability-
Suppose R be a partial order on Sand a, b ∈S whenever aRb or bRa, we say that a A a and b are comparable otherwise a And b are non-comparable.
Q17) Find the number of ways to partition of 10 peoples into four groups 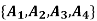
So that two teams contain 3 persons and two teams contain 2 persons.
A17)
By using above theorem, we get-

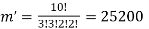 ordered partitions
ordered partitions
Here the group form an unordered partition so that we divide m’ by 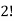 Because of the two cells with three elements each and
Because of the two cells with three elements each and 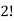 Because of the two cells with two elements each.
Because of the two cells with two elements each.
So that-

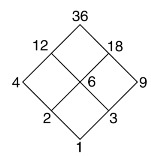
Q18) Draw the Hasse diagram of positive division of 36.
A18)
We have
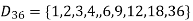
Suppose R is the partial order relation on 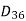
The Hasse diagram will be-
Q19) Show that the inverse of an invertible mapping is unique.
A19)
Let 
By any invertible mapping,
Let,
g: Y→X
h: Y→X
Are two different inverse mapping of f.
Let y ∈ Y and
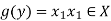
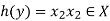
Now-
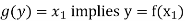
And
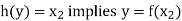
So that-
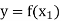 and
and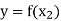
Now-
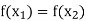
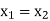
Which shows that g(y) = h(y)∀ y ∈ Y
So that the inverse of f is unique.
Q20) Show that addition is primitive recursive.
A20)
Addition is defined by a + 0 = a, a + (b + 1) = (a + b) + 1 for all natural numbers a a, b.
We define f (a, b) = a + b such that
f (a, b + 1) = a + b + 1 = (a + b) + 1
= f (a, b) + 1
= S (f (a, b))
Also f (a, 0) = a
We define f (a, b) as

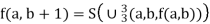
If follows that f comes from primitive recursion from 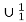 and
and 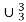 so that f is primitive recursive.
so that f is primitive recursive.