Unit - 2

Fuzzy set and fuzzy logic

Q1) What is fuzzy set?

A1)

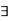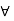In addition, we use "iff" as a shorthand expression of "if and only if," and the standard symbols and are used for the existential quantifier anti the universal quantifier, respectively. The characteristic function of a crisp set assigns a value of either 1 or 0 to each individual in the universal set, thereby discriminating between members and nonmembers of the crisp set under consideration. This function can be generalized such that the values assigned to the elements of the universal set fall within a specified range and indicate the membership grade of these elements in the set in question. Larger values denote higher degrees of set membership. Such a function is called a membership function, and the set defined by it a fuzzy set.

Q2) What is the membership function of fuzzy set?

A2)

Two distinct notations are most commonly employed in the literature to denote membership functions. In one of them, the membership function of a fuzzy set A is denoted by 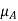, that is

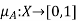
I n In the other one, the function is denoted by A and has, of course, the same form:

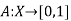
Q3) Describe the four family membership function.

A3)

The following are general formulas describing the four families of membership functions, where r denotes the real number for which the membership grade is required to be one (r = 2 for all functions in Fig.above), and 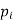(i belongs to 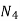) is a parameter that determines the rate at which, for each x, the function decreases with the increasing difference |r – x|:

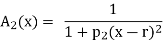
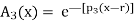
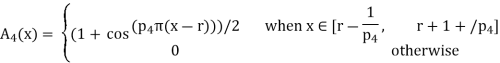
Q4) What is fuzzy variable?

A4)

Several fuzzy sets representing linguistic concepts such as low, medium, high, and so on are often employed to define states of a variable. Such a variable is usually called a fuzzy variable.

The significance of fuzzy variables is that they facilitate gradual transitions between states and, consequently, possess a natural capability to express and deal with observation and measurement uncertainties.

Q5) What are interval-valued fuzzy sets?

A5)

Interval-valued fuzzy sets can further be generalized by allowing their intervals to be fuzzy. Each interval now becomes an ordinary fuzzy set defined within the universal set [0, 1]. Since membership grades assigned to elements of the universal set by these generalized fuzzy sets are ordinary fuzzy sets, these sets are referred to as fuzzy sets of type 2.

Q6) What is trapezoidal membership?

A6)

In this section, we introduce some basic concepts and terminology of fuzzy sets. To illustrate the concepts, we consider three fuzzy sets that represent the concepts of a young, middle-aged, and old person. A reasonable expression of these concepts by trapezoidal membership functions

These functions are defined on the interval [0, 80] as follows:

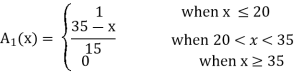
One of the most important concepts of fuzzy sets is the concept of an a-cut and its variant, a strong 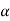-cut. Given a fuzzy set A defined on X and any number a belongs to [0, 1], the 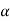cut, 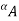, and the strong 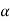-cut, 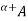, are the crisp sets

Q7) What are fuzzy complements?

A7)

Let A be a fuzzy set on X. Then, by definition, A(x) is interpreted as the degree to which x belongs to A. Let cA denote a fuzzy complement of A of type c. Then, cA (x) may be interpreted not only as the degree to which x belongs to cA, but also as the degree to which x does not belong to A. Similarly, A (x) may.'also be interpreted as the degree to which x does not belong to cA.

As a notational convention, let a complement cA be defined by a function

c : [0, 1] → [0, 1],

Which assigns a value c(A(x)) to each membership grade A(x) of any given fuzzy set A. The

Value c(A(x)) is interpreted as the value of cA(x). That is,

c(A(x)) = cA(x)

For all x E X by definition. Given a fuzzy set A, we obtain cA by applying function c to values A(x) for all x E X.

Q8) What is the relationship between the crisp set and fuzzy set?

A8)

A crisp relation represents the presence or absence of association, interaction or interconnectedness between the elements of two or more sets. This concept can be generalized to allow for various degrees or strengths of association or interaction between elements. Degrees of association can be represented by membership grades in a fuzzy relation in the same way as degrees of set membership are represented in the fuzzy set. In fact, just as the crisp set can be viewed as a restricted case of the more general fuzzy set concept, the crisp relation can be considered to be a restricted case of the fuzzy relation.

A relation among crisp sets X1, X2, ... , X, is a subset of the Cartesian product

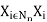
It is denoted either by R(XI, X2, ... , or by the abbreviated form R(Xi\i ∈ ℕn). Thus,

R(X1, X2, …, Xn) ⊆ X1× X2 × . . . × Xn

So that for relations among sets X1, X2, ... , X,,, the Cartesian product X1 x X2 x ... x X represents the universal set. Because a relation is itself a set, the basic set concepts such as containment or subset, union, intersection, and complement can be applied without modification to relations.

Each crisp relation R can be defined by a characteristic function which assigns a value of 1 to every tuple of the universal set belonging to the relation and a 0 to every tuple not belonging to it. Denoting a relation and its characteristic function by the same symbol R, we have

R(x1, x2, …, xn) =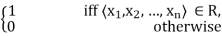

The membership of a tuple in a relation signifies that the elements of the tuple are related to or associated with one another. For instance, let R represent the relation of marriage between the set of all men and the set of all women. Of all the possible pairings of men and women, then, only those pairs who are married to each other will be assigned a value of 1 indicating that they belong to this relation. A relation between two sets is called binary; if three, four, or five sets are involved, the relation is called ternary, quaternary, or quinary, respectively. In general, a relation defined on n sets is called n-ary or n-dimensional. .

Q9) What is binary fuzzy relation?

A9)

Binary relations have a special significance among n-dimensional relations since they are, in some sense, generalized mathematical functions. Contrary to functions from X to Y, binary relations R (X, Y) may assign to each element of X two or more elements of Y. Some basic operations on functions, such as the inverse and composition, are applicable to binary relations as well.

Given a fuzzy relation R(X, Y), its domain is a fuzzy set on X, dom R, whose membership function is defined by

Dom R(x) =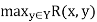

Q10) Define binary relations on a single set.

A10)

In addition to defining a binary relation that exists between two different sets, it is also possible to define a crisp or fuzzy binary relation among the elements of a single set X.

A binary relation of this type can be denoted by R(X, X) or R(X2) and is a subset of

X x X = X2. These relations are often referred to as directed graphs or digraphs.

Binary relations R (X, X) can be expressed by the same forms as general binary relations (matrices, sagittal diagrams, tables). In addition, however, they can be conveniently expressed in terms of simple diagrams with the following properties: (1) each element of the set X is represented by a single node in the diagram; (2) directed connections between nodes indicate pairs of elements of X for which the grade of membership in R is nonzero; and (3) each connection in the diagram is labeled by the actual membership grade of the corresponding pair in R. An example of this diagram for a relation R(X, X) defined on X = {1, 2, 3, 4) is shown in Fig. 5.4, where it can be compared with the other forms of representation of binary relations.

Various significant types of relations R(X, X) are distinguished on the basis of three different characteristic properties: reflexivity, symmetry, and transitivity. First, let us consider crisp relations.