Unit - 4

Graph theory

Q1) Explain the graph theory.

A1)

Graph theory is intimately related to many branches of mathematics. It is widely applied in subjects like, Computer Technology, Communication Science, Electrical Engineering, Physics, Architecture, Operations Research, Economics, Sociology, Genetics, etc. In the earlier stages it was called slum Topology. It also has uses in social sciences, chemical sciences, information retrieval systems, linguistics even in economics also.

Graphs are discrete structures consisting of vertices and edges that connects these vertices. There are several different types of graphs that differ with respect to the kind and number of edges that can a connect a pair of vertices. Problems in almost every conceivable discipline can be solved using graph models.

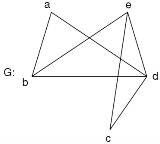
Q2) Consider the graphs given below-

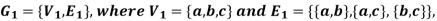
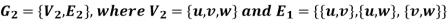
Check whether these graphs are same or not?

A2)

As we can see that these graphs are not same because here and are not same since 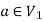but a does not belongs to .

These two graphs look same but not equal.

We can draw these graphs as below-

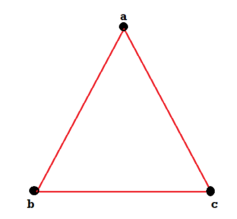
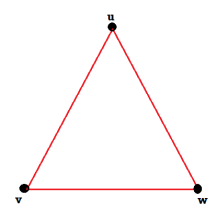
These types of graphs are known as isomorphic graph when they are same except for the name of vertices.

Q3) Define degree of vertex.

A3)

The number of edges incident on a vertex v is called degree of vertex v, with loop being counted twice.

We can denote it as-

Degree of v = d(v)

Q4) Define weighted graph.

A4)

A graph G is said to be a weighted graph if each edge e of G is assigned a non-negative number w(e) called the weight of v.

The weighted graph is given below-

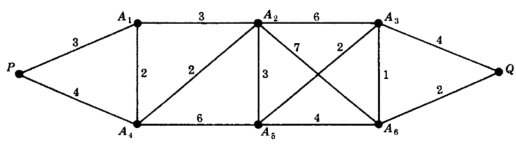
Q5) Define subgraph and isomorphic graph.

A5)

Sub Graphs-

We can say that is a sub-graph of G = (V, E), and write 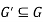provided .

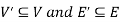We can say that 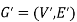is an induced sub-graph of G = (V, E), provided 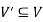and every edge in E whose vertices are still in is also an edge in .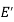

Isomorphic graphs-

Let 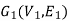and 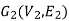be two graphs. The graph 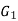and 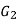are said to be isomorphic if there is a bijective function 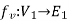such that if u and v are end vertices of some edge e ∈ then 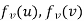end vertices of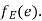

Q6) What are bipartite graphs?

A6)

A graph G(V, E) is said to be bipartite, if the vertex set V can be partitioned in to two non-empty disjoint subset 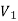and 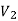such that each edge is G had end vertex is 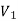and other end vertex in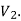

There is no edge between two vertices of 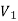as well as there is no edge between two vertices of .

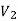Here 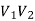bipartition of V.

Q7) What is Adjacency matrix of a non-directed graph?

A7)

Let G be a graph with n vertices and no parallel edges. The adjacency matrix of G in a n × n. Symmetric binary matrix A (G)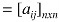 

Where

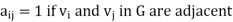
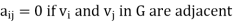
Where 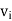and 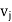are vertices of G.

The following is a example of the adjacency matrix of the simple graph G.

Adjacency matrix x; A (G)-

Q8) Define subgraph.

A8)

Let G and H be two graphs. H is called a subgraph of G if V (H) is a subset of V (G)

And E (H) is a subset of E (G).

If H is a subgraph of G then

(i) All the vertices of H are in G.

(ii) All the edges of H are in G.

(iii) Each edge of H has the same end points in H as in G.

Q9) Define isomorphic graphs.

A9)

Isomorphism of graphs: Two graphs are said to be isomorphic it they have identical behaviour in terms of graph-theoretic properties. More precisely:

Let Let G1 (V1, E1) and G2 (V2, E2) be two simple undirected graphs. A function f: V1 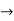 V2 is called a graph isomorphism if i) f is one-one and onto, i.e there exists a one-to-one correspondence between their vertices as well as edges (both the graphs have equal number of vertices and edges, however, vertices may have different levels.)

Ii) for all u,vV1, {u,v} E1 if and only if {f(u), f(v)} E2

If such a function exists, then the graphs G1 and G2 are called isomorphic graphs.

Q10) What is walk?

A10)

A walk is defined as a finite alternating requence of vertices and edges, begining and ending with vertices, such that each edge is incident with the vertices preceding and following it. Let u, v be any two vertices in an undirected graph G. Then a walk u-v in G is finite alternating sequence u-v1 e1 v2 e2 ... ... ... En vn = V of vertices and edges. Vertices with which a walk begins and ends are called terminal vertices.

Q11) Define path and circuit.

A11)

Path: An open walk in which no vertex appears more than once is called a path. The number of edges in a path is called the length of the path.

An edge which is not a loop is s path of length one. A loop can be included in a walk but not in a path.

Circuits: A circuit is a closed walk of non-zero length that contains no repeated edges except the initial and end vertex where intial and end vertex. That is, a circuit is a closed, nointersecting walk. A circuit is also called elementary cycle, circular path and polygon.

Q12) What are the connected graphs?

A12)

Connected graphs: A graph is said to be connected if we can reach any vertex from any other vertex by traveling along the edges. More formally: A graph is said to be connected if there exists at least one path between every pair of its vertices, otherwise, the graph is disconnected.

That is a graph G is connected if give any vertices u and v, it is possible to travel from u to v along a sequence of adjacent edges fig. Given above is connected

Graph but in fig. Above is a disconnected graph.

Q13) Define path.

A13)

Let G be a non-directed graph. A sequence P of zero or more edges of the form 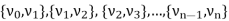, where 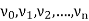are the vertices of G is called a path in G.

We denote this by P 

The vertex 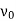is called the initial vertex and the vertex 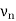is called the terminal vertex of the path P.

Q14) Explain edge connectivity.

A14)

Edge connectivity: Each cut-set of a connected graph G consists of a certain number of edges. The number of edges in the smallest cut-set

(i,e cut-set with fewest number of edges) is defined as the edge connectivity

Of G.

Equivalently the edge connectivity 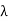(G) of a connected graph can be defined as the minimum number of edges whose removal reduces the graph disconnected. If G is a tree, then 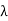(G) = 1, became removel of any one edges reduces the the tree disconnected.

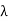(G) = 2

Q15) Define Eulerian graph.

A15)

A undirected graph with no isolated vertices is said to have an Euler circuit if there is a circuit in G that traverses every edge of the graph exactly once. If there is an open trail from vertex u to v in G and this trail traverses each edge in G exactly once, the trail is called Euler trail. [A trail from a vertex u to v is a path that doesnot involve a repeated edge] An Eulerian tour is a closed walk that starts at some vertex, passes through each edge exactly once and returns to the starting vertex.

Since any closed walk in an undirected graph enters and leaves any vertex the same number of times, the subgraph composed of the edges in any closed walk is even. Thus, if the graph contains a closed walk passing through each edge exactly once, the graph must be even, conversely, if the graph is even, then it contains an Euler tour, A path that passes through each edge exactly once but vertices may be repeated is called Euler path. A graph that contains an Euler tour or Euler circuit is called an Eulerian graph.

Q16) Define Hamiltonian graph.

A16)

Hamiltonian graph: Let G be a connected graph with more than two vertices. If there is a path in G that uses each vertex of the graph exactly once, then such a path is called Hamiltonian path. If the path is a circuit that contains each vertex in G exactly once, except the initial vertex, then such a path is called a Hamiltonian circuit.

A graph that contains a Hamiltonian circuit is called a Hamiltonian graph.

Q17) Define tree.

A17)

The concept of a tree is important for these interested in applications of graphs. The important applications of trees include searching, sorting, syntax checking and database management. The tree is one of the most non-linear structures used for algorithm development in computer science. In this section, we shall define a tree and study its properties.

Definition of a tree- A tree is a connected graph without any circuits.

A graph is acyclic, if it has no cycles.

A tree is a connected acyclic graph. i, e a tree is a simple graph having neither a self-loop nor parallel edges. Trees with three, four and five vertices are given in fig.

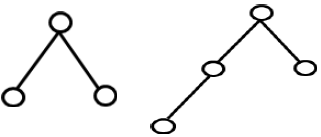
Q18) Prove that, in any tree with two or more vertices there are at least two pendant vertices.

A18)

Let T be a tree with n vertices, then T has n–1 edges,

Again, we know that,

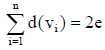
Where e is the number of edges in T

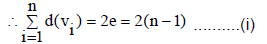
Since no vertex of T can be of zero degree. So, from (1), we must have at least two vertices of degree one in T. It means taht in any tree with two or more vertices there are at least two pendant vertices.

Q19) What is the distance and centres in a tree?

A19)

Distance and centres in a tree: In a connected graph G, the distance d(u,v) between two of its vertices u and v is the length of the shortest path. i,e the number of edges in the shortest path between them. It is very easier to determine the distance between any two vertices of a tree because, there is exactly one path between any two vertices of the tree.

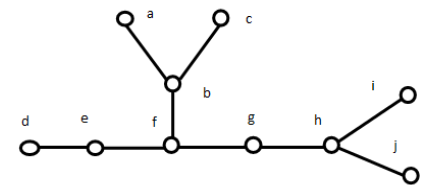
The graph in fig., d (a, b) = 1, d (a, d) = 4, d(b, h) = 3, d (a, j) = 5 and so on.

The eccentricity E (v) of a vertex v in a, graph G is the distance from

v to the vertex farthest from v in G, i.e E(v) = max {d(u,v) : uv}

The graph in fig. E(a) = 5, E(b) = 4, E(f) = 3, E(g) = 3, E(h) = 4 and so one.

A vertex with minimum eccentricity in a graph G is called the centre

Of G.

The diameter of a tree is the maximum distance between any two vertices of the tree.

Q20) What are the spanning trees?

A20)

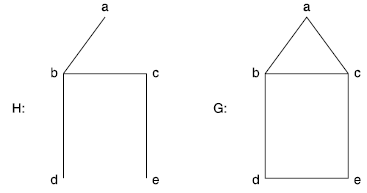
Let G be a connected graph. The sub-graph H of G is called a spanning tree of G if

(i) H is a tree and (ii) H contains all the vertices of G.

Example: In the Fig. Below H is spanning tree of G.

Sol:

Q21) A non-directed graph G is connected if and only f G contains a spanning tree.

A21)

Let T be a spanning tree of G. There exists a path between any pair of vertices in G along the tree T. G is connected.

Conversely let G be a connected graph and K be the number of cycles in G. If K = 0, then G has no cycles and G is connected. Therefore G is a tree when K = 0.

Let us suppose that all connected graphs with fewer than K cycles have a spanning tree. Let G be a connected graph with n cycles. Let e be an edges in one of the cycle. G – e is a connected graph and

G – e contains all the vertices of G.

∴ The spanning tree if G – e is also spanning tree for G.

Hence by mathematical induction the result holds for all connected graphs.

If G is a connected graph and T is a spanning tree of G. Edges of G present in T are called the branches of G with respect to Tj and the edges of G which do not belong to T are called the chords of G with respect to T. If G has n vertices and e edges then, the number of branches with respect to the spanning tree T of G is n – 1 and the number of chords is e – n + 1.

The number of branches in a connected graph G is called the rank of G and the number of chords is called the nullity of G. If G has k components then the rank of G is defined as the sum of ranks of the components; i.e.,

Where Gi, i = 1, 2, ..., K are K components of G. And nullity of

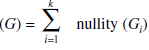
Q22) What is Kruskals algorithm?

A22)

Input: A connected weighted graph G with n vertices.

Step 1: Arrange the edges of in order of increasing weights and select the edge with minimum weight.

Step 2: Proceed sequentially, add each edge which does not result in a cycle until n – 1, edges are selected.

Step 3: Exit.