UNIT 4:

UNIT 4:

UNIT 4:

Q 1:

The equation of the curve passing through the origin and satisfying the equation

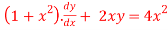  is

Solution:

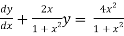
It is the linear equation of the form

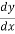+ Py =Q

Here  p=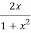   and Q=

I.F =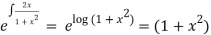

  the general solution is given by

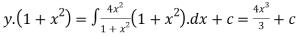
But it passes through(0,0) ,therefore c=0, hence the curve is

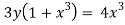
Q 2:

Find the solution for the following differential equation =

Solution:

The given D.E is of the form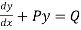

SO I.F is =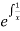

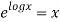
Hence the required solution is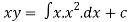

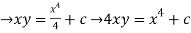
Q 3:

Find the solution for the following D.E

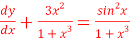
Solution:

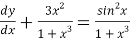
Here p=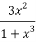  

I.F =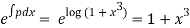

Thus the solution is,

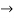
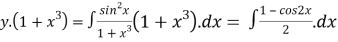
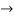
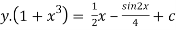
Q 4:

Solve the following D.E

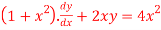
Solution:

It is the linear equation of the form

Dividing the given D.E on both sides by (1+x2)

So we get,

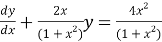
Now we have P=  and Q=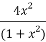

It is in the linear equation of the form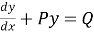

I.F =

The required reduced linear equation is,

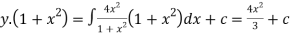
But it passes through(0,0) therefore c=0,hence the curve is 3y( =4x3

Q 5:

Solve the D.E 

Solution:

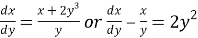, which is a linear equation of the form

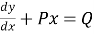
So I.F is 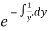and the general solution is,

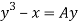
Where  A can be positive or negative.

Q 6:

Solve 

Solution:

The given equation is exact because the partial derivatives are the same:

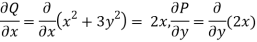
We have the following system of equations ,

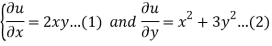
By integrating equation 1 w.r.to x.,

Substituting this expression for u(x,y) in eq(2) we get,

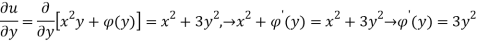
By integrating the above equation we get an unknown function

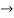
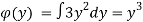
Then the general equation is,

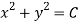,where c is an arbitrary constant.

Solve the given D.E  and test for convergence:

 Q8:

Solution:

Test for exactness:

Consider,

We have the following system of equations ,

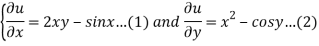
By integrating equation 1 w.r.to x.,

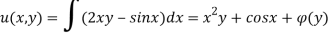
Substituting this expression for u(x,y) in eq(2) we get,

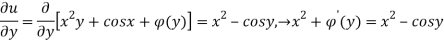
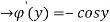
By integrating the above equation we get an unknown function

Then the general equation is,

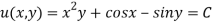
Q 9:

Solve the differential equation y’’’+2y’’-y’-2y=0

Solution:

The corresponding characterstic equation is,

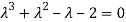
Solving it, we find the roots

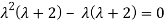
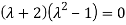
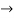
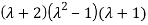=0

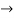
=-1

The general solution for the differential equation is

Y(x)=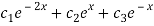

Where are arbitrary constants.

Q 10:

Solve the equation y’’’+11y’-5y=0

Solution:

The characterstic equation of the give D.E is

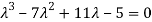
Here one of the root is 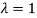then factorising the term  from the equation we obtain

((

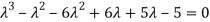
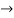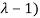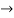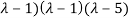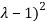( =0

((=0

Thus the equation has two roots

Hence the general equation of the D.E is

Y(x)=(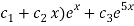

Where are arbitrary constants.

Q 11:

To find the general solution of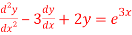 

Solution:

The characteristic  equation is r2 -3r+2 =0

The factors are (r-1)(r-2)=0

  r=1or r=2

Hence the general solution is A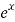+B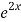

So in this case the fundamental solutions and their derivatives are as followas:

Y1(x)  = ex

Y1’(x) = ex

Y2(x) =e2x

Y2’(x) =2.e2x

Q 12:

Find the general solution of the following D.E

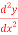-y=2-3

Solution :

Consider ,

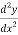-y=0

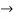  The characteristic equation is  r2 -1 =0

The factors are (r-1)(r+1)=0

  r= 1or-1

Hence the general solution is  A+B

Y1(x) = ex

Y1’(x) =ex

Y2(x) =e-x

Y2’(x) =-e-x

Q 13:

Finding the optimal current of an electrical circuit(RL circuits) in which the initial condition is i=0 at t=0

Solution:

By Kirchhoff voltage law(KVL) method,we get

The differential equation for the RL circuit will be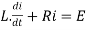

In which initial conditions are i=0  at t=0

The standard form of the equation is,
 

Dividing the differential equation by L  to obtain

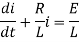
The integrating factor is

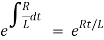
Multiplying the above equation with standard form gives rise to

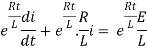
By applying integration on both sides we get

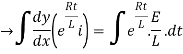
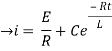
Now applying i=0 at t-0 gives us

0=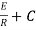

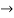C=-

NOW

i=

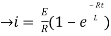  = t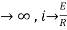

Therefore by finding current of the RL circuits is   i=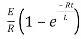

Hence we complete the solution by first order differential equation of first order and even several types of networking circuits and fluid mechanics uses this method.