UNIT 5
UNIT 5
UNIT 5
Q1:Solve the differential equation y’’’+2y’’-y’-2y=0
Solution:
The corresponding characteristic equation is,

Solving it, we find the roots
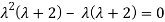
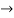


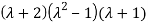 =0
=0

 =-1
=-1
The general solution for the differential equation is
Y(x)= 
Where 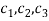 are arbitrary constants.
are arbitrary constants.
Q 2:Solve the equation y’’’+11y’-5y=0
Solution:
The characteristic equation of the give D.E is
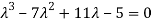
Here one of the root is 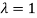 then factorising the term
then factorising the term  from the equation we obtain
from the equation we obtain
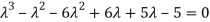
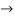 (
( (
(
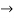 (
(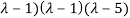 =0
=0
 (
(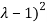 (
( =0
=0
Thus the equation has two roots 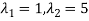
Hence the general equation of the D.E is
Y(x)=(
Where  are arbitrary constants.
are arbitrary constants.
Q 3: To find the general solution of 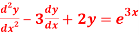
Solution:
The characteristic equation is r2 -3r+2 =0
The factors are (r-1)(r-2)=0
 r=1or r=2
r=1or r=2
Hence the general solution is A +B
+B
So in this case the fundamental solutions and their derivatives are as followas:
Y1(x) = ex
Y1’(x) = ex
Y2(x) =e2x
Y2’(x) =2.e2x
Q 4:Find the general solution of the following D.E
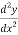 -y=2
-y=2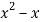 -3
-3
Solution :
Consider ,
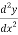 -y=0
-y=0
 The characteristic equation is r2 -1 =0
The characteristic equation is r2 -1 =0
The factors are (r-1)(r+1)=0
 r= 1or-1
r= 1or-1
Hence the general solution is A +B
+B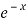
Y1(x) = ex
Y1’(x) =ex
Y2(x) =e-x
Y2’(x) =-e-x
Q 5:Find the value of m for the following D.E
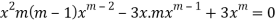
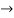
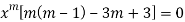
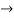 m (m-1)-3m+3=0
m (m-1)-3m+3=0
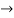 m2 – 4m +3=0
m2 – 4m +3=0
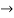 (m-1)(m-3)=0
(m-1)(m-3)=0
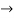 m= 1, 3
m= 1, 3
Q 6:Solve y’=(y+1)x
=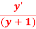 =x
=x
= 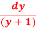 = xdx
= xdx
By integrating on both sides we get,
Ln(y+1) =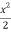 +c
+c
1+y=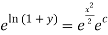
 y(x)=
y(x)=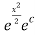 -1
-1
Q 7:Find the Legendre’s equation for the following D.E
 -
-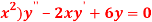
Solution:
n(l+n)=6 , n=2
c2 = -
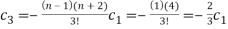
For k= 2,3,....
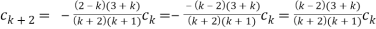
At k=2, 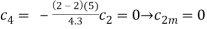 for m=2,3,.....
for m=2,3,.....
 the general solution is.,
the general solution is.,
Y=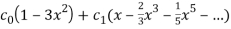
= 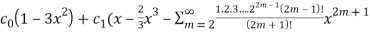
Q 8:Solve the given D.E
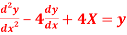
Solution:
The above equation can be writen as,
(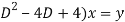 ....... (1)
....... (1)
( ........ (2)
........ (2)
Eliminating y from equations (1) and (2)
( (
(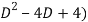 x=25x+16et
x=25x+16et
i.e.
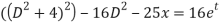
 (
(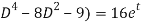

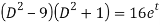
 x=A.
x=A.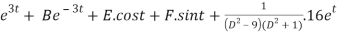
Thus the general equation is,
A.e3t +B.e-3t+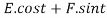 -et.
-et.
Q 10:Solve the following equations using Legendre’s method:
(1).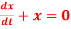
(2).
Solution:
Subtract eq(1)-eq(2)
i.e the given equations can be written as follow:
Dx+y=0......(1)
Dy+x=0.......(2)
(1) Dx+y=0 (
Dx+y=0 ( (2)
(2) D
D Dx+D2y=0
Dx+D2y=0
By subtracting the above two equations we get.,
y-D2y=0
 (D2 -1)y =0
(D2 -1)y =0
 The general solution is given by,
The general solution is given by,
Aet+Be-t.
Q 11:Verify that  and
and  both satisfy the constant co-efficient linear homogeneous equation:
both satisfy the constant co-efficient linear homogeneous equation:
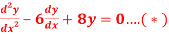
Solution:
Consider, 
Differenting on both sides we get,
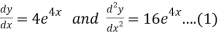
Now consider, 
Differenting on both sides we get,
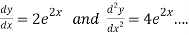 (2)
(2)
Substituting eq(1) and (2) in equation(*) we get the general solution as follow,
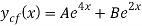
Q 12:Find the order and degree of the following D.E
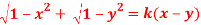
Solution:
Let x= sin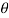 and y=sin
and y=sin
Then the given equation can be written as,
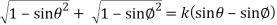
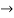 (
(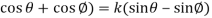
 2cos
2cos


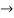



On differentiating both sides we get,
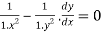
Q 13:A spring with spring constant 18N/m is attached to a 2kg mass with negligible friction. Determine the period that the spring mass system will oscillate for any non-zero initial conditions.
Solution:
From above, we have a spring mass system modelled by the DE
2y’’ + 18y = 0 which has general solution given by
y(t) = 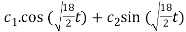 = c1 cos(3t)+c2 sin(3t)
= c1 cos(3t)+c2 sin(3t)
Since period of cost is 2π, then the period of cos(3t) and sin(3t) is 2π/ 3 .
Therefore, the period of c1 cos(3t) + c2 sin(3t) is also 2π /3 .
Q 14:Two 9-volt batteries are connected to a series in which the inductance is ¼ henry and the resistance is 8 ohms. Determine the current i(t) if the initial current is zero.
Solution:
Given,
L= R=8 E(t)=18
R=8 E(t)=18
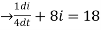
The required D.E is,
L .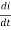 +Rt=E(t)
+Rt=E(t)
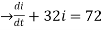
U(t) = 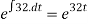

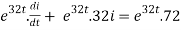
 the above equation can be written as,
the above equation can be written as,
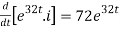
Q 15: Given: The rectangular beam, built in at the left end, having length, L, and cross-section of width, b, and height, h, is acted upon by a point load, P, at its free end.
Req'd: Determine the deflection at the end of the beam. 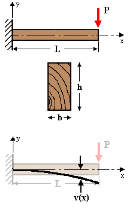
Sol'n: The bending moment in the beam is given by:
M(x)=-P(L-x)
Therefore the differential equation for bending is:
Elv”(x)=-P(L-x)
Integrating with respect to x
Elv’(x)=-P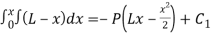
Since the slope at the built-in end is zero, then
v’(x=0)=0 =0
=0
Integrating again gives:
Elv(x)= -P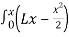 dx= -P
dx= -P +
+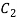
The deflection at the built-in end is zero, therefore:
v(x=0)=0 .
.
Therefore, the equation of the elastic curve is:
v(x)= 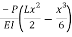
Deflection at the tip is then:
v(L)=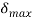 =
=
Since the sign of v(L) is negative, the deflection is downward.