UNIT 6:

UNIT 6:

UNIT 6:

Q 1: Express in the form of a + ib :

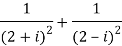
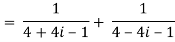
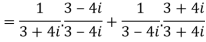
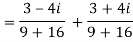
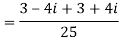
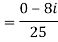
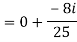
Q 2: find the modulus of

Solution:

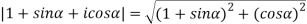
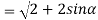
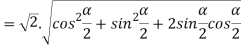
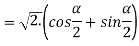
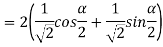
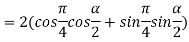
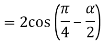
Q 3:

If 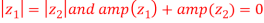then show that are   conjugate complex numbers?

Solution:

       Let

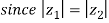
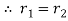
Also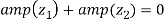

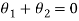
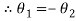
Again

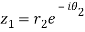
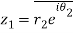
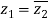
Hence both of them are conjugate to each other.

Q 4:

If 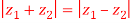, then show that the difference of the amplitude ofand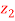

Is

Solution:

Let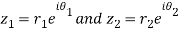

|

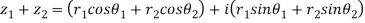
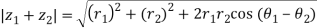
Similarly

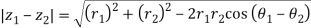
So,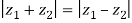

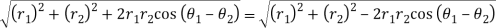
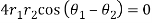
          So,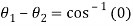

   Therefore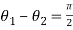

Try: If 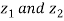be two complex numbers. Show that

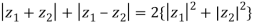
Q 5: If 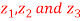be the vertices of an isosceles triangle, right angled at , prove that

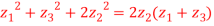
Solution:

The triangle ABC is isosceles A

BC when rotated with 90 degree coincide

With BA.

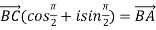
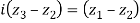
Squaring on both sides

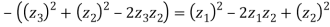
So,

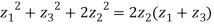
Equation of a circle in the complex plane:

The equation of the circle in the complex plane is given by

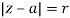
Where the center of the circle is point “a”  and  radius of circle is “r”.

Q 6:

Problem: simplify 16 i+10i (3-i)

Solution:

Given,

16i +10i (3-i)

=16i+10i(3i)+10i(-i)

=16i+30i-10i2

=46i-10(-1)

=46i+10

Here real part is 10 and imaginary part is 46

Q 7:

Problem: express the following into a+ib form

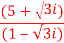
Solution:

Given.,  

z  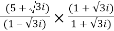 =  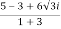    = = + i

Modulus , = = = 

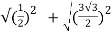Conjugate = (  - 

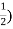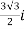
1. Find the value of

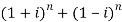
Sol: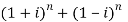

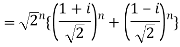
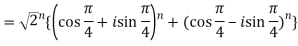
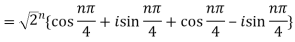
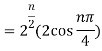
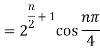
Q 8:   Find the value of

Sol:  

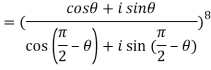
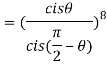
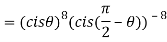
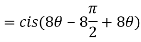
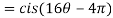
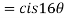
Q 9: If

Then find out the values of : a)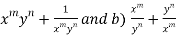

Sol: Let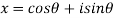

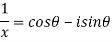
By Demoviers theorem

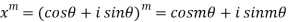
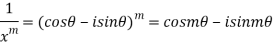
Similarly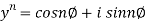

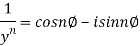
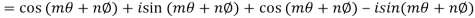
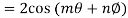
Q 10: Prove that

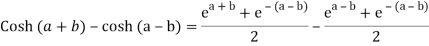
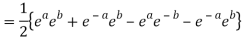
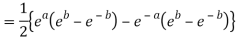
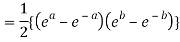
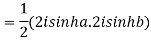
Q 11: If ,show that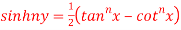

                            Given

                            Taking exponential on both side

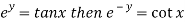
                          Taking nth power on both sides

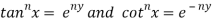
                        RHS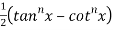  

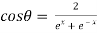
Q 12: If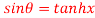 then prove that

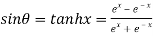……(i)

                         Squaring both sides

                          Now,

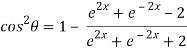
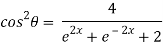
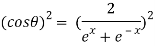
……(ii)

                  Dividing (i) by (ii)

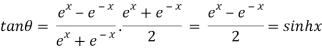
Q 13: Find the value of ?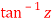

       Let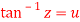

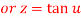
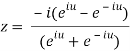
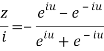
            By componendo and dividendo we get

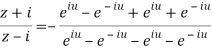
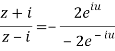
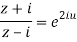
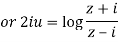
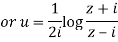
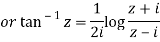
Q 14: Prove that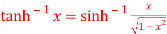

                       Let

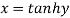
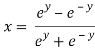
                       Squaring on both sides

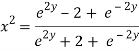
              Again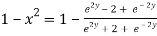   

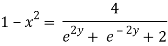
                    Taking square root on both side

            Now,

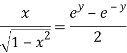
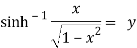
           Hence 

Q 15:Prove that

                        Let 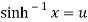….(i)

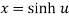
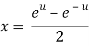
                            Squaring both side

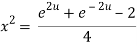
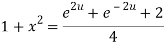
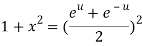
                        Taking square root on both side

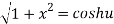
  …….(ii)

Again  

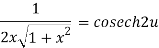
……(iii)

                      Now,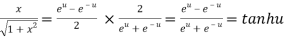 

   ……(iv)

                    From all above equation we get

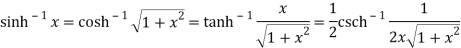
Q 16:

(i)                Prove that sinlog (i-1) = 1

Solution:

Let i-1 =

log (i-1) = log (eπ/2) =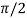

  Sin log (i-1) = sin (π/2) =1

(ii)              Prove that

=

=

=   

=   

=   

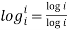
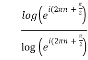
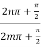
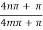
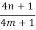
=R.H.S

Q 17:

Separate the real and imaginary parts of 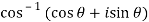and also show that the angle is positive and acute angle?

Sol: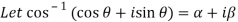  

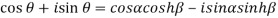
                        Equating real and imaginary parts we get

…..(1)

….(2)

             Squaring and adding (1) and (2) we get

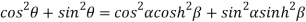
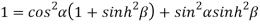
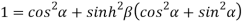
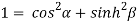
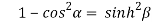
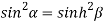…..(3)

From equation(2)

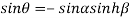
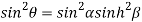
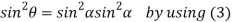
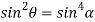
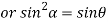
Hence is positive and acute angle.

Q 18:  Separate the real and imaginary part of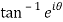

                          Let )….(1)

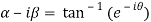…..(2)

                             On adding (1) and (2) we get

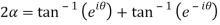
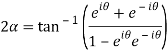
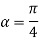
                        Subtracting (1) and(2) we get

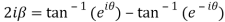
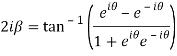
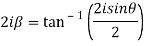
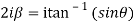
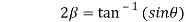
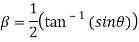
           Which are the required real and imaginary parts.