UNIT I
Quantum Mechanics
- Explain Davisson - Germer Experiment.
The first experimental evidence of matter waves was given by two American physicists, Davisson and Germer in 1927.
The apparatus consists of an electron gun G where the electrons are produced. When the filament of electron gun is heated up electrons are emitted due to thermionic emissions. Now, the electrons are accelerated in the electric field of known potential difference. These electrons are collimated by suitable slits to obtain a fine beam which is then directed to fall on a large single crystal of nickel, known as target T which is rotated about an angle along the direction of the beam is detected by an electron detector (Faraday cylinder) which is connected to a galvanometer. The Faraday cylinder ‘c’ can move on a circular graduated scale between 290 c to 900 to receive the scattered electrons.
Fig: Davisson and Germer’s experimental arrangement
First of all, the accelerating potential V is given a low value and the crystal is set at any orbital azimuth (θ). Now the Faraday cylinder is moved to various positions on the scale’s’ and galvanometer current is measured for each position. A graph is plotted between galvanometer current against angle θ between incident beam and beam entering the cylinder. The observations are repeated for different acceleration potentials.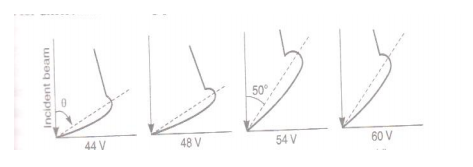
Fig:
It is observed that a ‘bump’ begins to appear in the curve for 44 volts. Following points are observed.
(a) With increasing potential, the bump moves upwards.
(b) The bump becomes most prominent in the curve for 54 volts at θ = 500.
(c) At higher potentials, the bumps gradually disappear.
The bump in its most prominent state verifies the existence of electron waves. According to de- Broglie, the wavelength associated with electron accelerated through a potential V is given by-
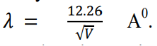
Hence, the wavelength associated with an electron accelerated through 54 volts is-
From X-ray analysis, it is known that a nickel crystal acts as a plane diffraction grating with space d = 0.91å According to experiment, we have diffracted electron beam at θ = 50˚ . The corresponding angle of incidence relative to the family of Bragg plane:
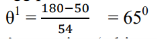
Using Bragg’s equation (taking n=1), we have
=2dsinθ
= 2(0.9Å) Sin 65˚
=1.65Å
This is in good agreement with the wavelength computed from de-Broglie hypothesis.
As the two values are in good agreement, hence, confirms the de-Broglie concept of matter waves.
2. Explain crompton’s effect.
In 1922, Arthur Compton studied the scattering of x-rays of known frequency from graphite and looked at the recoil electrons and the scattered x-rays.
According to wave theory, when an electromagnetic wave of frequency 
is incident on an atom, it would cause electrons to oscillate. The electrons would absorb energy from the wave and re-radiate electromagnetic wave of a frequency
. The frequency of scattered radiation would depend on the amount of energy absorbed from the wave, i.e. on the intensity of incident radiation and the duration of the exposure of electrons to the radiation and not on the frequency of the incident radiation. Compton found that the wavelength of the scattered radiation does not depend on the intensity of incident radiation but it depends on the angle of scattering and the wavelength of the incident beam. The wavelength of the radiation scattered at an angle θ is given by-
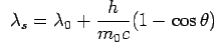
Where 
is the rest mass of the electron. The constant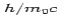 
is known as the Compton wavelength of the electron and it has a value 0.0024 nm. The spectrum of radiation at an angle θ consists of two peaks, one at
and the other at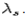
. Compton effect can be explained by assuming that the incoming radiation is a beam of particles with
- Energy-
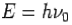
- Momentum –
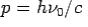
Consider a photon of energy
and momentum 
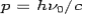colliding elastically with an electron at rest. Let the direction of incoming photon be along the x-axis. After scattering, the photon moves along a direction making an angle θ with the x-axis while the scattered electron moves making an angle φ. Let the magnitude of the momentum
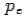of the scattered electron be while that of the
Scattered photon be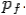
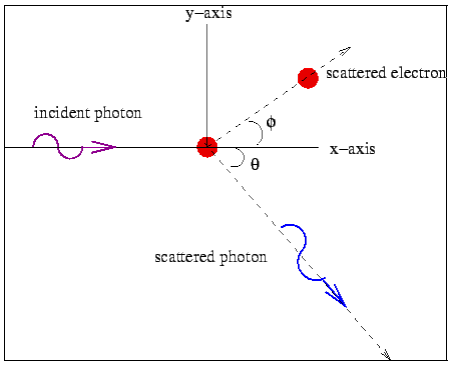
Conservation of momentum:
X- direction—
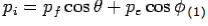---------Eq 1
Y- direction—
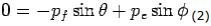---------Eq 2
From eq. 1 and 2—
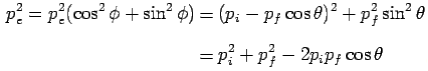---------Eq 3
Conservation of Energy:---
If the rest mass of electron is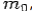 
and the initial energy is 
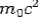and the final energy is
Then-
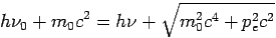--------Eq.4
On squaring Eq 4 we get--
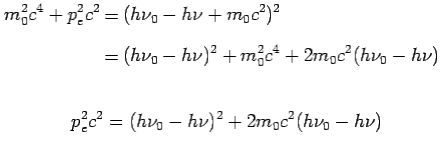
On substitute Eq 3 for 
we get—
Put the value of 
and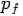 
we get—
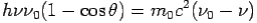
By using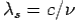 
We get Compton formula-
-
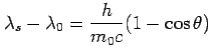
Here 
is known as Compton wavelength
3. Derive the Expression for de- Broglie wavelength.
The expression of the wavelength associated with a material particle can be derived on the analogy of radiation as follows:
Considering the plank’s theory of radiation, the energy of photon (quantum) is 
Where c is the velocity of light in vacuum and is its wave length.
According to Einstein energy – mass relation
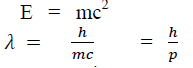
Where mc = p is momentum associated with photon.
If we consider the case of material particle of mass m and moving with a velocity v , i.e momentum mv, then the wave length associated with this particle ( in analogy to wave length associated with photon ) is given by
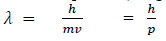
Different expressions for de-Broglie wavelength
(a) If E is the kinetic energy of the material particle then
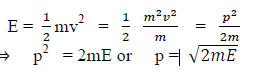
There for de Broglie wavelength is—
(b) When a charged particle carrying a charge ‘q’ is accelerated by potential difference v, then its kinetic energy K.E is given by
E = qV
Hence the de-Broglie wavelength associated with this particle is
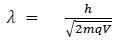
For an electron
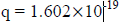
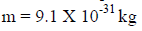
4. Distinction between matter waves and electromagnetic waves
S.no. | Matter wave | Electromagnetic wave | ||
1
2
3
4
5 |
Matter wave require medium for propagation i.e., they cannot travel through vacuum. | Electromagnetic waves are produced only by accelerated charged particles
Wavelength depends on the energy of photon
Travel with velocity of light c= 3×108 m/s
Electric field and magnetic field oscillate perpendicular to each other.
Electromagnetic waves do not require medium |
4. Explain Bohr’s quantisation condition.
Bohr three postulate are following: -
1. Electron in an atom moves in circular orbits, obeying classical mechanics, about the nucleus under Coulomb interaction thus obeying classical electromagnetic theory.
2. Of all the infinite set of orbits possible in classical mechanics, electron moves only in those for which its orbital angular momentum is an integral multiple of h/2π, i.e. L = nh, which is a departure from classical mechanics. Further, electron moving in such an orbit does not loose energy by electromagnetic radiation, though it is in accelerated motion, thereby defying classical electromagnetic theory on the way.
3. Electromagnetic radiation is emitted if electron, initially moving in an orbit with energy Ei , jumps discontinuously to another orbit of energy Ef and the frequency of the emitted radiation is ν = (Ei − Ef )/h.
Based on these postulates of Bohr, calculation of the energy of an atomic electron moving in one of the allowed orbits is straight forward. From postulate 1, an electron of charge −e and mass m moving round a nucleus of charge Ze and mass M in an orbit of radius r with velocity v, we get--
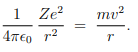
From postulate 2, we get--
These two together give us---
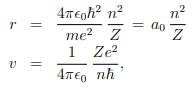
Where, a0 ≈ 5.3nm is known as Bohr radius. The ratio between the speed of electron in the first Bohr orbit (n = 1) and the speed of light is equal to a dimensionless constant α, known as fine structure constant:
Which actually gives the strength of electromagnetic coupling. Now the kinetic and potential energy of this electron are
Therefore, the total energy of the electron, E = K + V , moving in an orbit specified by n is-
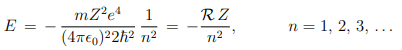
i.e. the quantization of orbital angular momentum leads to quantization of orbital energy. R = 13.6eV is called Rydberg constant. From postulate 3, the frequency of electromagnetic radiation emitted when the electron makes transition from quantum state (Ei , ni) to the quantum state (Ef , nf ) is ---
The above expression explains the discrete atomic spectral lines i.e. discrete frequency of electromagnetic radiation when electron jumps around among the discrete energy levels of the atom.
