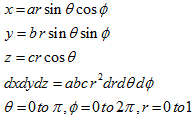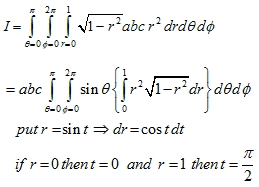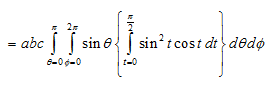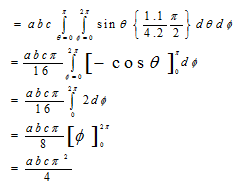Unit - 3

Multiple integrals and their applications

Q1) Evaluate 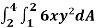, where dA is the small area in xy-plane.

A1)

Let ,     I =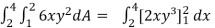 

=

= 

= 

=  84 sq. Unit.

Which is the required area,

Q2) Evaluate

A2)

Let us suppose the integral is I,

I =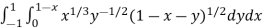

Put c = 1 – x in I, we get

I =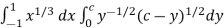

Suppose, y = ct

Then dy = c

Now we get,

I =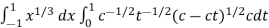

I =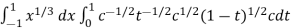

I =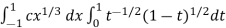

I =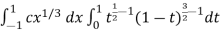

I  =

As we know that by beta function,

Which gives,

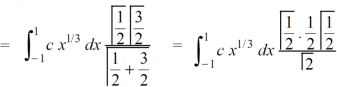
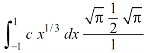
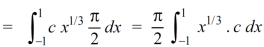
Now put the value of c, we get

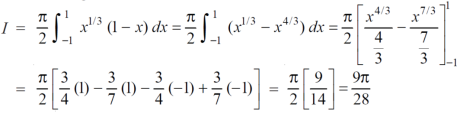
Q3) Evaluate-

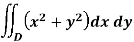
Where D is bounded by y = x and .

A3)

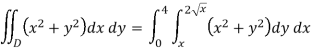
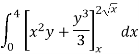
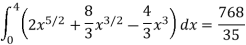
Q4) Evaluate the following by changing to polar coordinates,

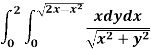
A4)

In this problem, the limits for y are 0 to and the limits for are 0 to 2.

Suppose,

y =

Squaring both sides,

y² = 2x - x²

x² + y² = 2x

But in polar coordinates,

We have,

r² = 2r cosθ

r = 2 cosθ

From the region of integration, r lies from 0 to 2 cosθ  and θ varies from 0  to π / 2.

As we know in case of polar coordinates,

Replace x by r cosθ and y by r sinθ, dy dx by r drdθ,

We get,

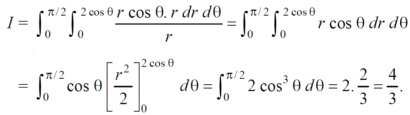
Q5) Evaluate the following integral by converting into polar coordinates.

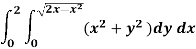
A5)

Here limits of y,

y =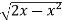

y² = 2x - x²

x² + y² = 2x

x² + y² - 2x = 0  ………………(1)

Eq. (1) represent a circle whose radius is 1 and centre is ( 1, 0)

Lower limit of y is zero.

Region of integration in upper half circle,

First we will covert into polar coordinates,

By putting

x by r cos θ and y by r sinθ ,  dy dx by r drdθ,

Limits of r are 0 to 2 cosθ  and limits of  θ  are from 0  to π / 2.

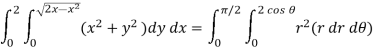
Q6) Evaluate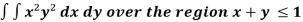

A6)

Let the integral,

I =

=

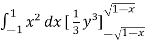
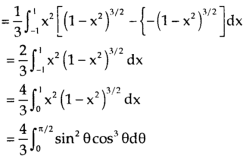
Put x = sinθ

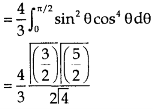
= π / 24   ans.

Q7) Evaluate-

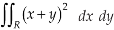
Where-

R is the region bounded by a parallelogram- x + y = 0, x + y = 2, 3x – 2y = 0, 3x – 2y = 3.

A7)

By changing the variables x, y to the new variables u and v, by the substitution x + y = u, 3x – 2y = v, the given parallelolgram R reduces to a rectangle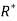

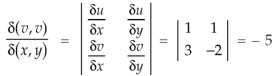
The required Jacobian is-

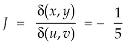
Since u = x + y and  u = x + y = 2, here u varies from 0 to 2  while v varies from 0 to 3.

Since-

3x – 2y = v = 0, 3x – 2y = v = 3

Therefore the integral will be in new variables-

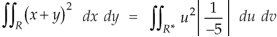
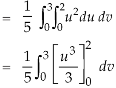
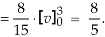
Which is the required answer.

Q8) Evaluate the transformation is x = v and y = uv.

A8)

Here the region of integration R is the triangle which is bounded by y = 0, x = 1 and y = x

Here put,

X = u and y = uv, we get-

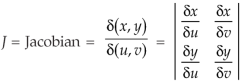
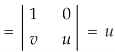
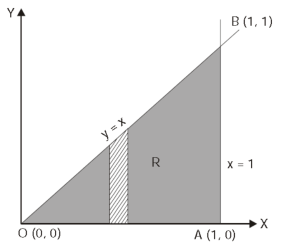
Here x varies from 0 to 1 while y varies from 0 to x.

Since u = x so u varies from 0 to 1

Here, similarly, since , so that v varies from 0 to 1. Thus-

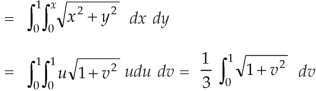
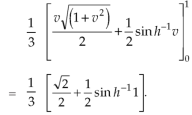
Q9) Change the order of integration for the integral 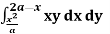 and evaluate the same with reversed order of integration.

A9) 

Given,

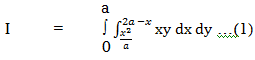
In the given integration, limits are

y = 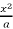, y = 2a – x and x = 0,   x = a

The region bounded by x2 = ay, x + y = 2a   

And x = 0, x = a is as shown in Fig.

Here we have to change order of Integration. Given the strip is vertical.

Now take horizontal strip SR.

To take total region, Divide region into two parts by taking line y = a.  

1 st Region:

Along strip, y constant and x varies from x = 0 to x = 2a – y. Slide strip IIelto  x-axis therefore y varies from y = a to y = 2a.

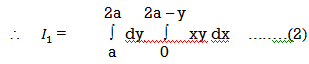
2nd Region:

Along strip, y constant and x varies from x = 0 to x= 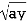. Slide strip IIel to x-axis therefore x-varies from y = 0 to y = a.

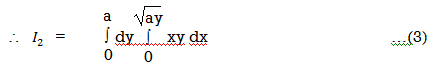
From Equation (1), (2) and (3),

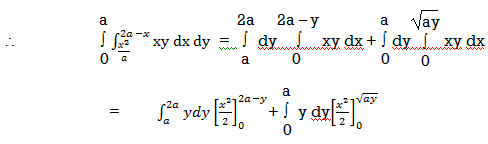
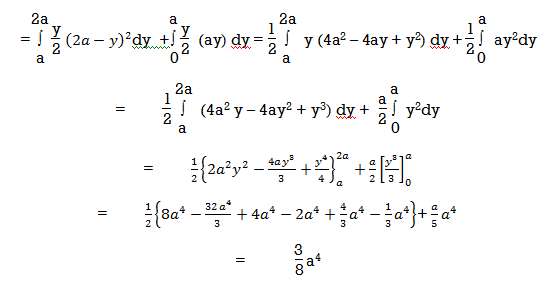
Q10) Determine the area enclosed by the curves-

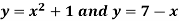
A10)

We know that the curves are equal at the points of interaction, thus equating the values of y of each curve-

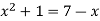
Which gives-

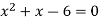
By factorization,

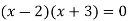
Which means,

x = 2 and x = -3

By determining the intersection points the range the values of x has been found-

x	-3	-2	-1	0	1	2
1	10	5	2	1	2	5

And

We get the following figure by using above two tables-

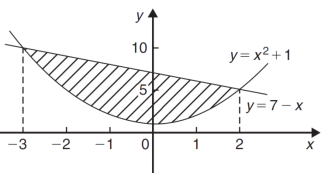
Area of shaded region =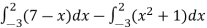

=

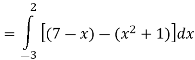
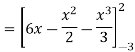
= ( 12 – 2 –  8/3 ) – (-18 – 9/2 + 9)

=

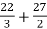
= 125/6 square unit

Q11) Determine the area bounded by three straight lines y = 4 – x, y = 3x and 3y = x

A11)

We get the following figure by using the equations of three straight lines-

y = 4 – x, y = 3x and 3y = x

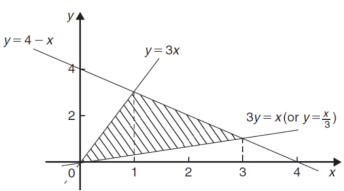
Area of shaded region-

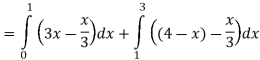
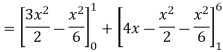
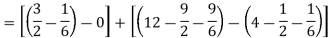
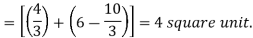
Q12) Find the area enclosed by the two functions-

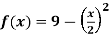and g(x) = 6 – x

A12)

We get the following figure by using these two equations

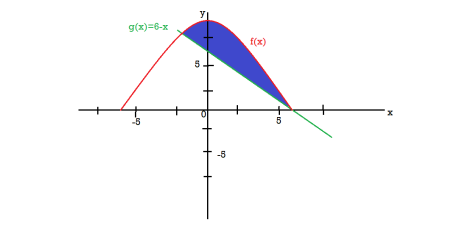
To find the intersection points of two functions f(x) and g(x)-

f(x) = g(x)

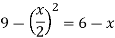
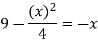
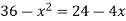
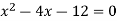
On factorizing, we get-

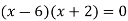
x = 6, -2

Now

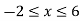
Then, area under the curve-

A =

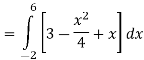
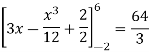
Therefore the area under the curve is  64/3  square unit.

Q13) Find the area enclosed by the curves and if the area is rotated about the x-axis then determine the volume of the solid of revolution.

A13)

We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-

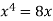
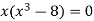
We get,

x = 0 and x = 2

The curve of the given equations will look like as follows-

Then,

The area of the shaded region will be-

A =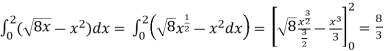

So that the area will be 8/3 square unit.

The volume will be

= (volume produced by revolving 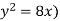– (volume produced by revolving

=

Q14) Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1,3].

A14)

The graph of the function f(x) = 1/x will look like-

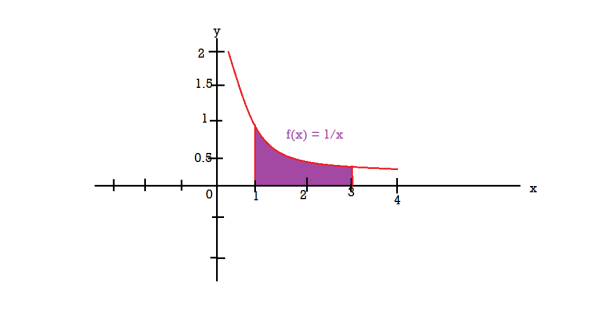
The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3]

Then the volume of the solid will be-

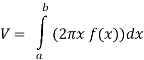
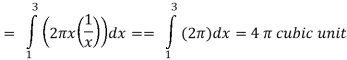
Q15) Find the mass of a plate formed by the coordinate planes and the plane-

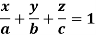
The variable density

A15)

Here we the mass will be-

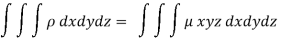
The limits of y are from y = 0 to y = b(1 – x/a) and limits of x are from 0 to a.

Therefore the required mass will be-

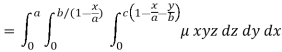
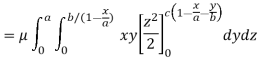
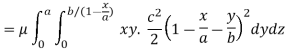
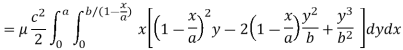
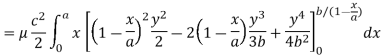
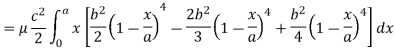
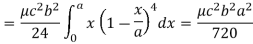
Which is the required answer.

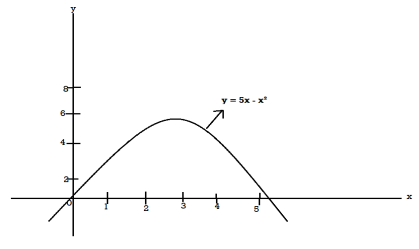
Q16) Determine the coordinates of the centroid of the area lying between the curve y = 5x - x² and the x-axis.

A16)

Here y = 5x - x²when y = 0, x = 0 or x = 5

Therefore the curve cuts the x-axis at 0 and 5 as in the figure-

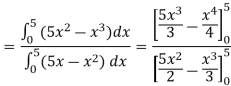
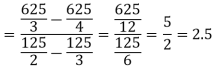
Now

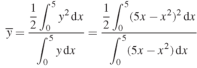
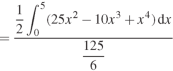
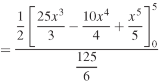
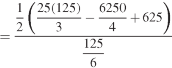
= 2.5

Therefore the centroid of the area lies at (2.5, 2.5)

Q17) Evaluate

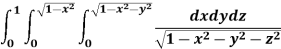
A17)

Let

I     =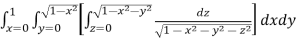    

=    

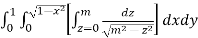
(Assuming m =  )

= dxdy

=

=

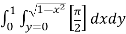
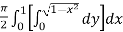
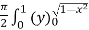= dx

=  dx

= 

=

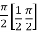
I =

Q18) Evaluate

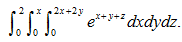
A18)

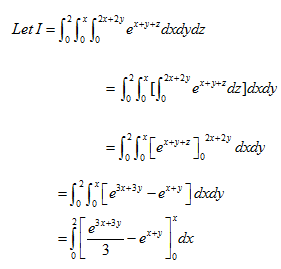
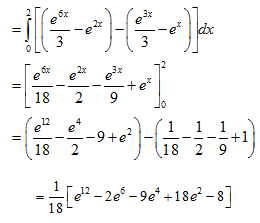
Q19) Evaluate

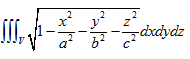
Throughout the volume of the ellipsoid

A19)

Put