Unit - 2

Equations of Equilibrium

Q1) Explain Coplanar concurrent and non concurrent forces.

A1)

The forces which meet at one point & their lines of action also lie on the same plane are called as coplanar concurrent force system.

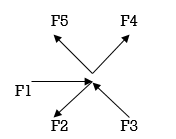
Coplanar nonconcurrent forces:

The forces which do not meet at one point but their line of action lies on the same plane are known as coplanar non-concurrent system of force.

Q2) Determine the forces in all members of truss by joint method

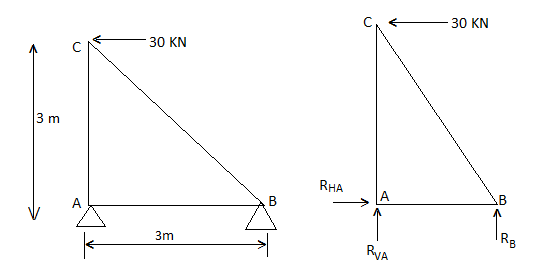
A2)

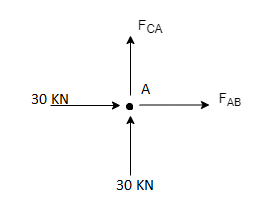
Consider FAB of Truss, Applying conditions of equilibrium,

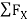= 0

RHA + 30 Kn

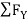= 0

 RvA + RB =0

Taking moment at point A,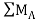 = 0

-(RB* 3) - (30*3) = 0

RB = -30 KN

RB =30 KN                      RVA = 30 KN

Consider Joint c, assuming forces in member AC & BC to be

Tensile, applying conditions of equilibrium,

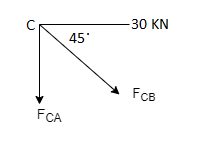
= 0

-30 + FCB cos 45 =0

FCB =30/cos 45 = 42.42 KN (T)

= 0

- FcA – FCB sin 45=o

-F CA -42.42 sin 45 =0     

-FCA – 30= 0

-FCA = -30 KN

Consider Joint c, assuming forces in member AC & BC to be

Tensile, applying conditions of equilibrium,                                        

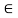Fx = 0 30+FAB =0

FAB = -30KN

Q3) The uniform crate shown in Fig. Below has a mass of 20 kg. If a force P = 80 N is applied to the crate, determine if it remains in equilibrium. The coefficient of static friction is s= 0.3.

A3)

The first step is free-body diagram i.e.

Free-Body Diagram. As shown in Fig. Diagram below, the resultant normal force NC acts at a distance of x from the centre line of crate for countering the tilting effect caused by P. Hence, there are three unknowns, F, NC and x, which can be solved by equations of equilibrium.

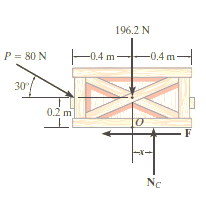
Equations of equilibrium:

Σ Fx = 0

80 cos 30° N - F = 0

Σ Fy = 0

-80 sin 30° N + NC - 196.2 N = 0

Σ M = 0

80 sin 30° N10.4 m2 - 80 cos 30° N10.2 m2 + NC (x) = 0

Thus, solving the above equations, we get,

F = 69.3 N

NC = 236 N

x = -0.00908 m = -9.08 mm

As value of x is negative, hence it acts to left of centre line of the crate. There will be no tipping since x < 0.4 m. Fmax = Nc = 0.3(236 N) = 70.8 N. Since F that we got is 69.3 N < 70.8 N, the crate will not slip.

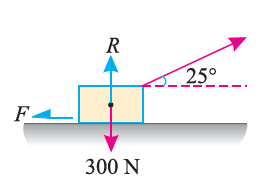
Q4) A body of weight 300 N is lying on a rough horizontal plane having a coefficient of friction as 0.3. Determine the magnitude of the force, which is needed to move the body, acting at 25° by the horizontal.

A4)

Given:

Weight of the body (W) = 300 N; Coefficient of friction (μ) = 0.3 and

Angle made by the force with the horizontal (α) = 25°

Let P = Magnitude of the force, which can move the body, and

F = Force of friction.

Initially, we will solve the problem in horizontal direction as,

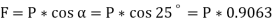
The next step is to resolve the force in vertical direction, we get,

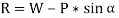
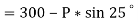
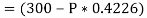
The force of friction (F) is given as,

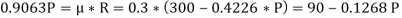
Or
 

Hence, P = 87.1 N.

Q5) A body, which is positioned on a rough horizontal plane, needs a pull of 180 N inclined at 30° to the plane just for moving. Also, it was found that a push of 220 N which is inclined at 30° to the plane also moved the body. Find out the weight of the body and the coefficient of friction present here.

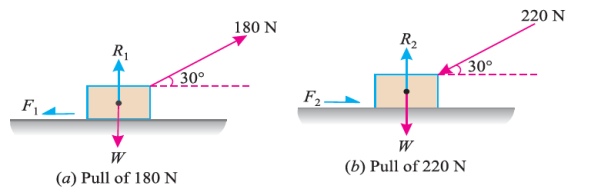
A5)

Given: Pull = 180 N; Push = 220 N and angle at which force is inclined with horizontal plane (α) = 30°

Let W = Weight of the body

R = Normal reaction, and

μ = Coefficient of friction.

First of all, consider a pull of 180 N acting on the body. We know that in this case, the force of friction (F1) will act towards left as shown in Fig. (a).

Resolving the forces horizontally,

F1 = 180 cos 30° = 180 × 0.866 = 155.9 N

And now resolving the forces vertically,

R1 = W – 180 sin 30° = W – 180 × 0.5 = W – 90 N

We know that the force of friction (F1),

155.9 = μR1 = μ (W – 90)

Now consider a push of 220 N acting on the body. We know that in this case, the force of friction (F2) will act towards right as shown in Fig. (b).

Resolving the forces horizontally,

F2 = 220 cos 30° = 220 × 0.866 = 190.5 N

And now resolving the forces horizontally,

R2 = W + 220 sin 30° = W + 220 × 0.5 = W + 110 N

We know that the force of friction (F2),

190.5 = μ.R2 = μ (W + 110) ...(ii)

Dividing equation (i) by (ii)

155.9 W + 17 149 = 190.5 W – 17 145

34.6 W = 34 294

W = 991.2 N

Now substituting the value of W in equation (i),

155.9 = μ (991.2 – 90) = 901.2 μ

μ = 0.173

In this way, numerical based on dry friction can be solved.

Q6) Draw FBD of a bar supported and loaded as shown below.

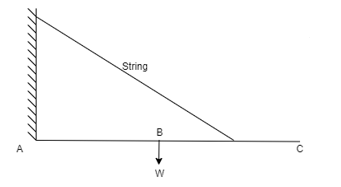
A6)

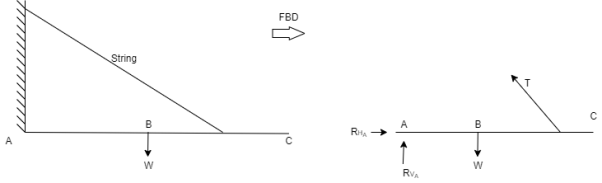
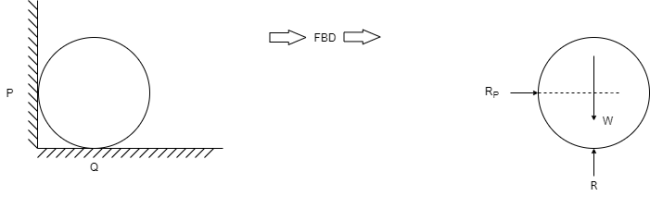
Q7) Draw FBD of sphere supported as shown below.

A7)

Q8) Find the axial force in the bar AB & AC as shown in figure.

A8)

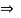Consider the free body diagram of all forces at B.

Q1 = tan -1   = 51.34º

Q2 = tan-1 = 45º

Let the forces developed in the member AB & AC are FAB &FBC respectively. The force diagram will be as follows at B.

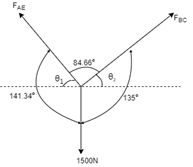
Applying Lami’s Theorem:

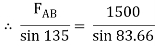
FAB = 1067.19 N

FBC = 942.81 N

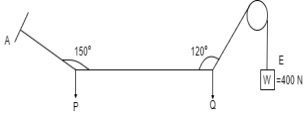
Q9) Find the tensions in the string AB, BC, CD, DE of the given system as shown in figure. String BC is horizontal & pulley D is frictionless.

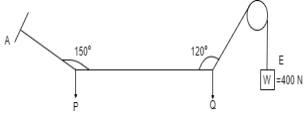
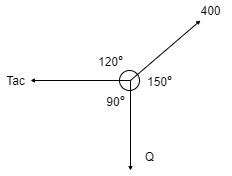
A9)

The string passes over the pulley & is attached to weight w = 400 N.  

Thus TCD = TDE = 400 N

Consider joint C & apply Lami’s theorem

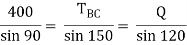
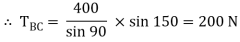
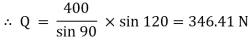
Now consider FBD at joint B

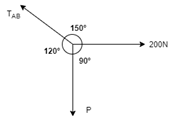
By using Lami’s theorem

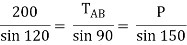
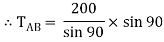
TAB = 230.94 N

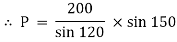
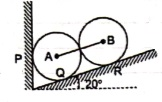
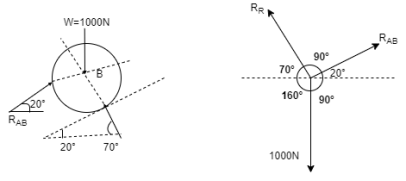
Q10) Two identical spheres having weight 1000 N are kept in a container as shown in figure. Find the reaction at all contact surfaces.

A10)

Consider the free body diagram of sphere B as shown below:

By lami’s theorem

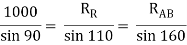
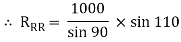
RRR = 939.69 N

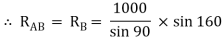
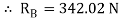  = RAB

Now consider FBD of sphere A

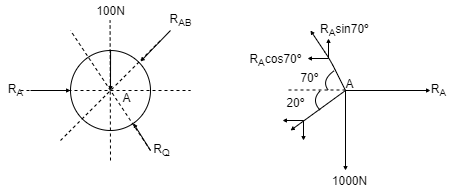
∑Fx = 0

-RB cos 20 – RQ cos 70 + Rp = 0

-342.02 cos 20 – RQ sin 70 + Rp  = 0

Rp = 321.39 + 0.34 RQ          ------------------(1)

∑ fy = 0

RQ sin 70 – 342.02 sin 20 – 1000 = 0

RQ = 1188.66 N    - put in equation (1)

Rp = 725.5 N

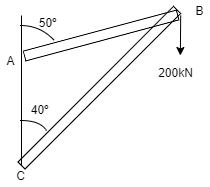
Q11) Two members AB & BC are supporting a load of 200 kN as shown in figure. Find the forces developed in the members AB & BC

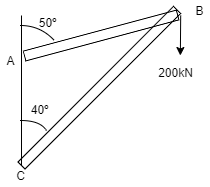
A11)

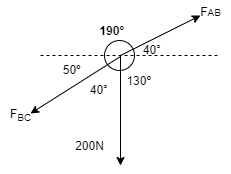
Consider the free body diagram of joint B as shown in figure

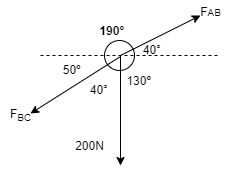
Assume that member BC is in compression & AB is in tension. By using Lami’s theorem at B,

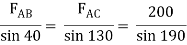
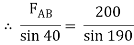
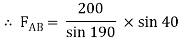
FAB = -740.33 kN 

-ve sign indicates that member AB is not in Tension but is in compression.

Now,

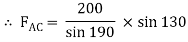
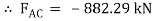
-ve sign indicates that member BC is not in compression but in tension.

Q12) A Sphere of weight 200 N rests on a smooth inclined plane. A sphere is kept in equilibrium by means of cable as shown. Find tension in cable and reaction.

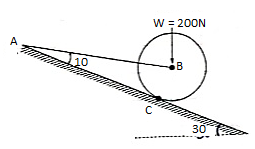
A12)

Consider the FBD of sphere B as shown in figure above.

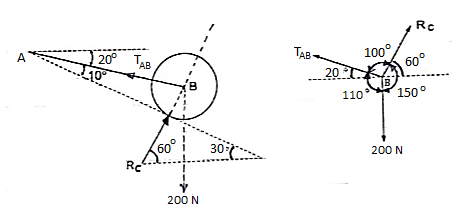
Applying lami’s theorem, we have

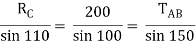
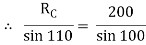
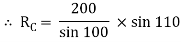
RC = 190.84 N

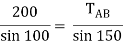
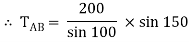
TAB = 101.54 N

Q13) The bar AB supports a load of 500 kN as shown in figure. The bae is kept in equilibrium by means of horizontal rope. Find tension in rope and reaction at A,

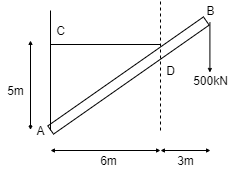
A13)

Consider the FBD as shown

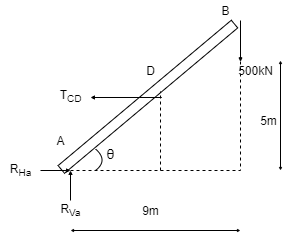
Applying conditions of equilibrium,

∑fx = 0

RHA – TCD = 0

RHA = TCD ------- (1)

∑fy = 0

RVA – 500 = 0

RVA = 500 kN

Taking moment about point A,

∑MA = 0

-(TCD × 5 ) + (500 × 9) = 0

-TCD × 5 = -4500

TCD =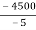

TCD = 900 kN

Putting the value in equation (1)

RHA = TCD

RHA = 900 kN

Q14) A bar of weight 200 N is hinged at A and pulled by the string attached at B as shown in figure. The length of bar is 5m. Find the support reactions at A & corresponding tension in string.

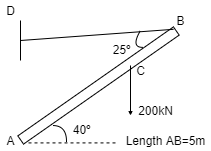
A14)

Consider triangle AEC

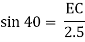
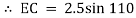
EC = 1.61 m

Consider triangle AEC

AE = 1.92 m

Applying conditions of equilibrium

∑fX = 0

-TBD cos15 + RHA = 0 -------- (1)

∑fy = 0

RVA – 200 – TBD sin15 = 0

RVA – 200 – 0.26TBD = 0 ----------(2)

Taking moment at A

∑MA = 0

-(TBD cos15 × 3.2) + (TBD sin15 × 3.84) + (200 × 1.92) = 0

-3.09 TBD + 0.99 TBD + 384 = 0

-2.1 TBD = -384

TBD = 182.86 N              ---put in (1) & (2)

RHA = TBD cos15 = 182.86 cos15

RHA = 196.62 N

RVA = 200 + 0.26TBD = 200 + (0.26 × 182.86)

RVA = 247.54 N

Unit - 2

Equations of Equilibrium

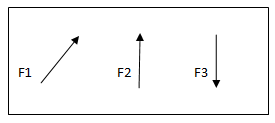
Q1) Explain Coplanar concurrent and non concurrent forces.

A1)

The forces which meet at one point & their lines of action also lie on the same plane are called as coplanar concurrent force system.

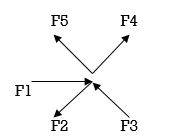
Coplanar nonconcurrent forces:

The forces which do not meet at one point but their line of action lies on the same plane are known as coplanar non-concurrent system of force.

Q2) Determine the forces in all members of truss by joint method

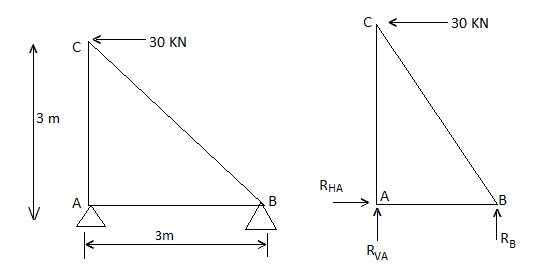
A2)

Consider FAB of Truss, Applying conditions of equilibrium,

= 0

RHA + 30 Kn

= 0

 RvA + RB =0

Taking moment at point A,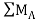 = 0

-(RB* 3) - (30*3) = 0

RB = -30 KN

RB =30 KN                      RVA = 30 KN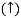

Consider Joint c, assuming forces in member AC & BC to be

Tensile, applying conditions of equilibrium,

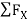= 0

-30 + FCB cos 45 =0

FCB =30/cos 45 = 42.42 KN (T)

= 0

- FcA – FCB sin 45=o

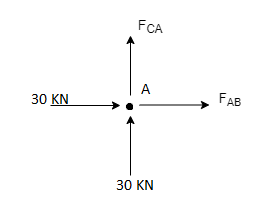
-F CA -42.42 sin 45 =0     

-FCA – 30= 0

-FCA = -30 KN

Consider Joint c, assuming forces in member AC & BC to be

Tensile, applying conditions of equilibrium,                                        

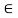Fx = 0 30+FAB =0

FAB = -30KN

Q3) The uniform crate shown in Fig. Below has a mass of 20 kg. If a force P = 80 N is applied to the crate, determine if it remains in equilibrium. The coefficient of static friction is s= 0.3.

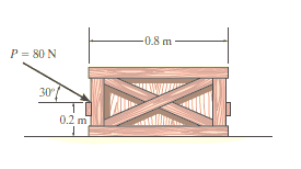
A3)

The first step is free-body diagram i.e.

Free-Body Diagram. As shown in Fig. Diagram below, the resultant normal force NC acts at a distance of x from the centre line of crate for countering the tilting effect caused by P. Hence, there are three unknowns, F, NC and x, which can be solved by equations of equilibrium.

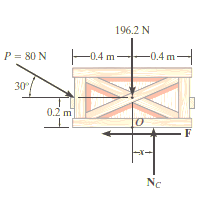
Equations of equilibrium:

Σ Fx = 0

80 cos 30° N - F = 0

Σ Fy = 0

-80 sin 30° N + NC - 196.2 N = 0

Σ M = 0

80 sin 30° N10.4 m2 - 80 cos 30° N10.2 m2 + NC (x) = 0

Thus, solving the above equations, we get,

F = 69.3 N

NC = 236 N

x = -0.00908 m = -9.08 mm

As value of x is negative, hence it acts to left of centre line of the crate. There will be no tipping since x < 0.4 m. Fmax = Nc = 0.3(236 N) = 70.8 N. Since F that we got is 69.3 N < 70.8 N, the crate will not slip.

Q4) A body of weight 300 N is lying on a rough horizontal plane having a coefficient of friction as 0.3. Determine the magnitude of the force, which is needed to move the body, acting at 25° by the horizontal.

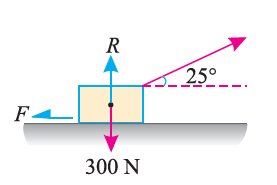
A4)

Given:

Weight of the body (W) = 300 N; Coefficient of friction (μ) = 0.3 and

Angle made by the force with the horizontal (α) = 25°

Let P = Magnitude of the force, which can move the body, and

F = Force of friction.

Initially, we will solve the problem in horizontal direction as,

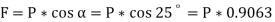
The next step is to resolve the force in vertical direction, we get,

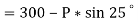
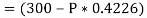
The force of friction (F) is given as,

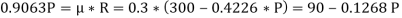
Or
 

Hence, P = 87.1 N.

Q5) A body, which is positioned on a rough horizontal plane, needs a pull of 180 N inclined at 30° to the plane just for moving. Also, it was found that a push of 220 N which is inclined at 30° to the plane also moved the body. Find out the weight of the body and the coefficient of friction present here.

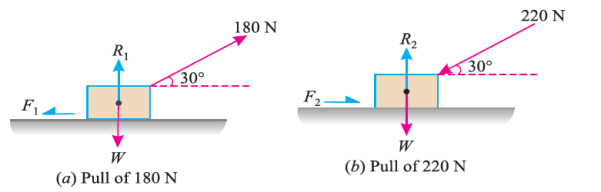
A5)

Given: Pull = 180 N; Push = 220 N and angle at which force is inclined with horizontal plane (α) = 30°

Let W = Weight of the body

R = Normal reaction, and

μ = Coefficient of friction.

First of all, consider a pull of 180 N acting on the body. We know that in this case, the force of friction (F1) will act towards left as shown in Fig. (a).

Resolving the forces horizontally,

F1 = 180 cos 30° = 180 × 0.866 = 155.9 N

And now resolving the forces vertically,

R1 = W – 180 sin 30° = W – 180 × 0.5 = W – 90 N

We know that the force of friction (F1),

155.9 = μR1 = μ (W – 90)

Now consider a push of 220 N acting on the body. We know that in this case, the force of friction (F2) will act towards right as shown in Fig. (b).

Resolving the forces horizontally,

F2 = 220 cos 30° = 220 × 0.866 = 190.5 N

And now resolving the forces horizontally,

R2 = W + 220 sin 30° = W + 220 × 0.5 = W + 110 N

We know that the force of friction (F2),

190.5 = μ.R2 = μ (W + 110) ...(ii)

Dividing equation (i) by (ii)

155.9 W + 17 149 = 190.5 W – 17 145

34.6 W = 34 294

W = 991.2 N

Now substituting the value of W in equation (i),

155.9 = μ (991.2 – 90) = 901.2 μ

μ = 0.173

In this way, numerical based on dry friction can be solved.

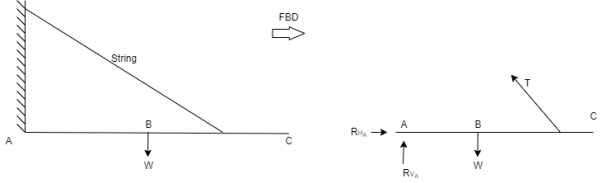
Q6) Draw FBD of a bar supported and loaded as shown below.

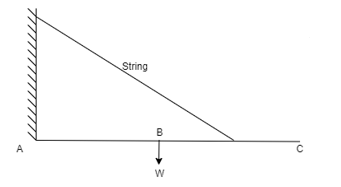
A6)

Q7) Draw FBD of sphere supported as shown below.

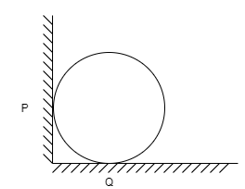
A7)

Q8) Find the axial force in the bar AB & AC as shown in figure.

A8)

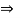Consider the free body diagram of all forces at B.

Q1 = tan -1 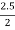  = 51.34º

Q2 = tan-1 = 45º

Let the forces developed in the member AB & AC are FAB &FBC respectively. The force diagram will be as follows at B.

Applying Lami’s Theorem:

FAB = 1067.19 N

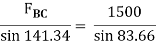
FBC = 942.81 N

Q9) Find the tensions in the string AB, BC, CD, DE of the given system as shown in figure. String BC is horizontal & pulley D is frictionless.

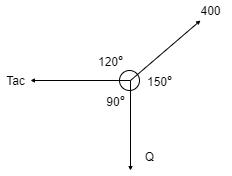
A9)

The string passes over the pulley & is attached to weight w = 400 N.  

Thus TCD = TDE = 400 N

Consider joint C & apply Lami’s theorem

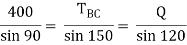
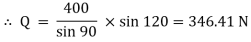
Now consider FBD at joint B

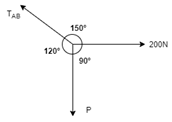
By using Lami’s theorem

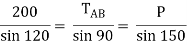
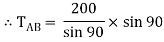
TAB = 230.94 N

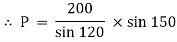
Q10) Two identical spheres having weight 1000 N are kept in a container as shown in figure. Find the reaction at all contact surfaces.

A10)

Consider the free body diagram of sphere B as shown below:

By lami’s theorem

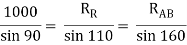
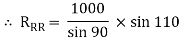
RRR = 939.69 N

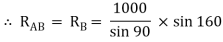
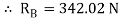  = RAB

Now consider FBD of sphere A

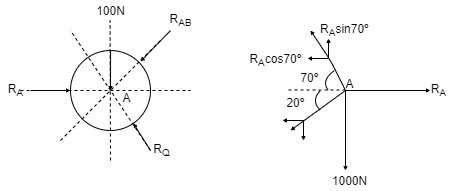
∑Fx = 0

-RB cos 20 – RQ cos 70 + Rp = 0

-342.02 cos 20 – RQ sin 70 + Rp  = 0

Rp = 321.39 + 0.34 RQ          ------------------(1)

∑ fy = 0

RQ sin 70 – 342.02 sin 20 – 1000 = 0

RQ = 1188.66 N    - put in equation (1)

Rp = 725.5 N

Q11) Two members AB & BC are supporting a load of 200 kN as shown in figure. Find the forces developed in the members AB & BC

A11)

Consider the free body diagram of joint B as shown in figure

Assume that member BC is in compression & AB is in tension. By using Lami’s theorem at B,

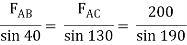
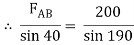
FAB = -740.33 kN 

-ve sign indicates that member AB is not in Tension but is in compression.

Now,

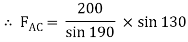
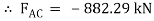
-ve sign indicates that member BC is not in compression but in tension.

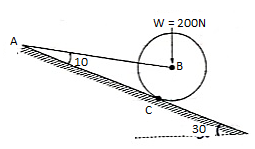
Q12) A Sphere of weight 200 N rests on a smooth inclined plane. A sphere is kept in equilibrium by means of cable as shown. Find tension in cable and reaction.

A12)

Consider the FBD of sphere B as shown in figure above.

Applying lami’s theorem, we have

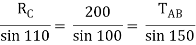
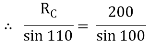
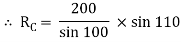
RC = 190.84 N

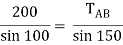
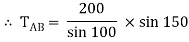
TAB = 101.54 N

Q13) The bar AB supports a load of 500 kN as shown in figure. The bae is kept in equilibrium by means of horizontal rope. Find tension in rope and reaction at A,

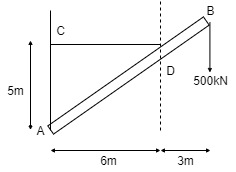
A13)

Consider the FBD as shown

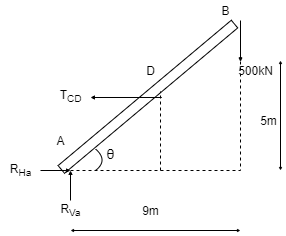
Applying conditions of equilibrium,

∑fx = 0

RHA – TCD = 0

RHA = TCD ------- (1)

∑fy = 0

RVA – 500 = 0

RVA = 500 kN

Taking moment about point A,

∑MA = 0

-(TCD × 5 ) + (500 × 9) = 0

-TCD × 5 = -4500

TCD =

TCD = 900 kN

Putting the value in equation (1)

RHA = TCD

RHA = 900 kN

Q14) A bar of weight 200 N is hinged at A and pulled by the string attached at B as shown in figure. The length of bar is 5m. Find the support reactions at A & corresponding tension in string.

A14)

Consider triangle AEC

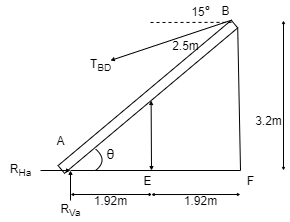
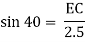
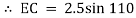
EC = 1.61 m

Consider triangle AEC

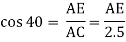
AE = 1.92 m

Applying conditions of equilibrium

∑fX = 0

-TBD cos15 + RHA = 0 -------- (1)

∑fy = 0

RVA – 200 – TBD sin15 = 0

RVA – 200 – 0.26TBD = 0 ----------(2)

Taking moment at A

∑MA = 0

-(TBD cos15 × 3.2) + (TBD sin15 × 3.84) + (200 × 1.92) = 0

-3.09 TBD + 0.99 TBD + 384 = 0

-2.1 TBD = -384

TBD = 182.86 N              ---put in (1) & (2)

RHA = TBD cos15 = 182.86 cos15

RHA = 196.62 N

RVA = 200 + 0.26TBD = 200 + (0.26 × 182.86)

RVA = 247.54 N