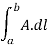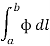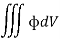Unit - 1
Review of Vector Analysis
Q1) Obtain the unit vector in the direction from the origin towards the point P(3,-3,-2)
A1)
The origin O(0,0,0) while P(3,-3,-2) hence the distance vector 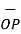 is
is
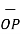 = (3-0)
= (3-0) 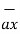 + (-3-0)
+ (-3-0) 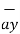 +(-2-0)
+(-2-0) 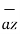 = 3
= 3  -3
-3 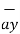 -2
-2 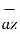
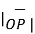 =
=  (3) 2 + (-3) 2 + (-2) 2 = 4.6904
(3) 2 + (-3) 2 + (-2) 2 = 4.6904
Hence the unit vector along the direction OP is
 OP=
OP= 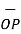 / |
/ |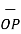 | = 3
| = 3 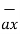 -3
-3 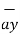 -2
-2 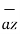 / 4.6904 =
/ 4.6904 =
= 0.6396 -0.63963
-0.63963 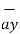 -0.4264
-0.4264 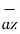
Q2) Given the three points in cartesian co-ordinate system as A(3,-2,1) B (-3,-3,5) , C (2,6,-4)
Find
i) The vector from A to C
Ii) The unit vector from B to A
Iii) The distance from B to C
Iv) The vector from A to the mid-point of the straight line joining B to C.
A2)
The position vectors for the given points are :
 = 3
= 3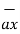 - 2
- 2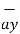 +
+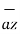 .
.
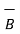 = -3
= -3 - 3
- 3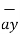 +5
+5 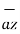 .
.
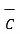 = 2
= 2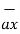 +6
+6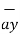 -4
-4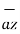 .
.
i) The vector from A to C is
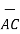 =
= 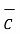 -
- 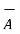 = [ 2-3]
= [ 2-3] 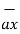 +[6–(-2)]
+[6–(-2)]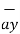 +[-4-1]
+[-4-1] 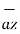 .
.
= - 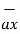 + 8
+ 8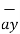 -5
-5 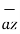 .
.
Ii) For unit vector from B to A obtain the distance vector 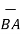 first
first
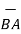 =
= 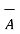 -
- 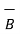
= [ 3 – (-3)] + [ (-2) –(-3) ]
+ [ (-2) –(-3) ] 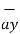 + [ -4-1]
+ [ -4-1] 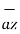
= 6 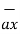 +
+ 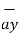 -4
-4  .
.
| | =
| = 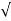 (6) 2 + (1) 2 + (-4)2 = 7.2801.
(6) 2 + (1) 2 + (-4)2 = 7.2801.
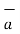 BA =
BA = 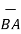 / |
/ |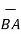 | = 6
| = 6  +
+ 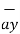 -4
-4 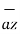 ./ 7.2801
./ 7.2801
Iii) For distance between B and C
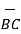 =
= 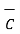 -
- 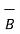 = [ 2 –(-3 ]
= [ 2 –(-3 ] 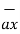 + [6-(-3)]
+ [6-(-3)] 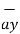 +[-4) –(-5)]
+[-4) –(-5)] 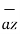 = 5
= 5 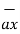 + 9
+ 9 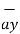 – 9
– 9 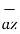
Distance BC = 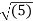 2 + (9) 2 + (-9) 2 = 13.6747
2 + (9) 2 + (-9) 2 = 13.6747
Iv) Let B(x1,y1,z1 ) and C(x2,y2,z2) then the co-ordinates of the mid-point BC are (x1+x2/2 , y1+y2/2 , z1+z2/2)
Q3) Evaluate 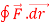 where F= cos y.i-x siny j and C is the curve y=
where F= cos y.i-x siny j and C is the curve y=  in the xy plae from (1,0) to (0,1)
in the xy plae from (1,0) to (0,1)
A3)
The curve y=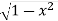 i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
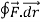 =
= 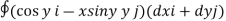
= 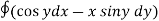
=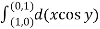 =-1
=-1
Q4) Evaluate 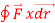 where
where 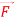 = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
A4)
F x dr = 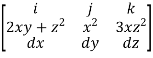
Put x=t, y=t2, z= t3
Dx=dt, dy=2tdt, dz=3t2dt.
F x dr = 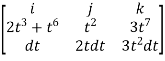
=(3t4-6t8) dti – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
=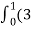 t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
=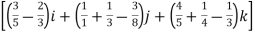
=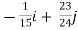 +
+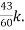
Q5) Prove that ͞͞͞F = [y2cos x +z3] i+(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for͞͞͞ F (ii) the work done in moving an object in this field from (0, 1, -1) to (π/ 2,-1, 2)
A5)
(a) The field is conservative if cur͞͞͞͞͞͞F = 0.
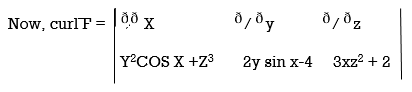
; Curl F= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =
(y2cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k = 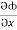 i +
i +  j +
j + 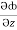 k
k
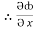 = y2cos x + z3,
= y2cos x + z3, 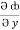 = 2y sin x – 4,
= 2y sin x – 4,  = 3xz2 + 2
= 3xz2 + 2
Now, 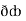 =
= 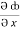 dx +
dx + 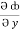 dy +
dy + 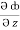 dz
dz
= (y2cos x + z3) dx +(2y sin x – 4)dy + (3xz2 + 2)dz
= (y2cos x dx + 2y sin x dy) +(z3dx +3xz2dz) +(- 4 dy) + (2 dz)
=d(y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =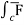 .d ͞r
.d ͞r
= 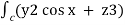 dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
= 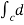 (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z ]( 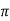 /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4 ] – { - 4 – 2} =4
+ 4 + 4 ] – { - 4 – 2} =4 + 15
+ 15
Q6) Evaluate 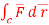 where
where  =yz i+zx j+xy k and C is the position of the curve.
=yz i+zx j+xy k and C is the position of the curve.
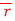 = (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
A6)
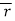 = (a cost)i+(b sint)j+ct k
= (a cost)i+(b sint)j+ct k
The parametric eqn. Of the curve are x= a cost, y=b sint, z=ct (i)
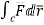 =
=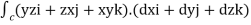
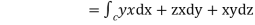
Putting values of x,y,z from (i),
Dx=-a sint
Dy=b cost
Dz=c dt
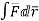 =
=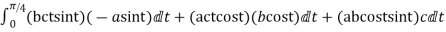
=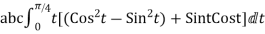
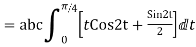
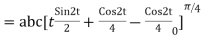
=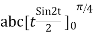 =
= 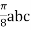
Q7) Find the circulation of  around the curve C where
around the curve C where  =yi+zj+xk and C is circle
=yi+zj+xk and C is circle 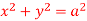 .
.
A7)
Parametric eqn of circle are:
x=a cos
y=a sin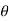
z=0
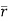 =xi+yj+zk = a cos
=xi+yj+zk = a cos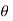 i + b cos
i + b cos + 0 k
+ 0 k
d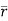 =(-a sin
=(-a sin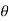 i + a cos
i + a cos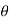 j)d
j)d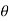
Circulation =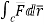 =
=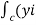 +zj+xk). d
+zj+xk). d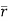
=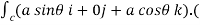 -a sin
-a sin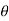 i + a cos
i + a cos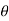 j)d
j)d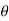
= =
= 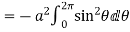
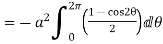

Q8) Evaluate  , where S is the surface of the sphere
, where S is the surface of the sphere 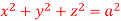 in the first octant.
in the first octant.
A8)
Here-
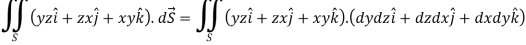

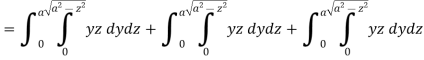
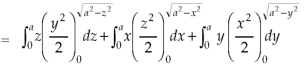
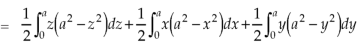
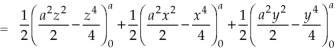
Which becomes-
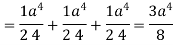
Q9) Evaluate 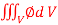 , where
, where  and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
A9)
Here- 4x + 2y + z = 8
Put y = 0 and z = 0 in this, we get
4x = 8 or x = 2
Limit of x varies from 0 to 2 and y varies from 0 to 4 – 2x
And z varies from 0 to 8 – 4x – 2y
So that-
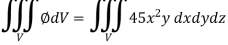
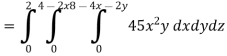
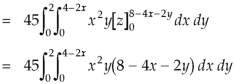

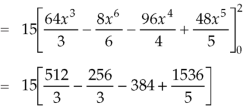
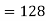
So that-
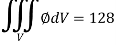
Q10) Evaluate 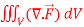 if V is the region in the first octant bounded by
if V is the region in the first octant bounded by 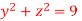 and the plane x = 2 and
and the plane x = 2 and 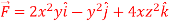 .
.
A10)
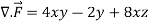
x varies from 0 to 2
The volume will be-
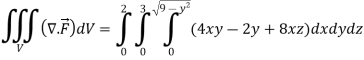

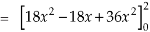
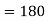
Q11) Find its gradient at P(0,1,1) for cartesian, 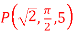 for cylindrical and
for cylindrical and  for the spherical.
for the spherical.
A11)
a) 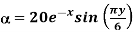 in Cartesian
in Cartesian
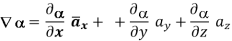
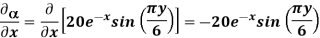
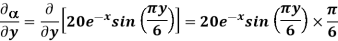
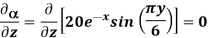
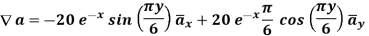
 At P (0,1,1) the
At P (0,1,1) the 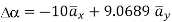
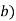
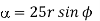 in cylindrical.
in cylindrical.
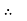 =
=
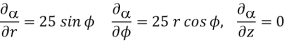
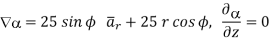
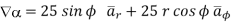
At 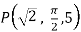 the =
the =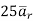
Q12) A scalar field is given by


A12)

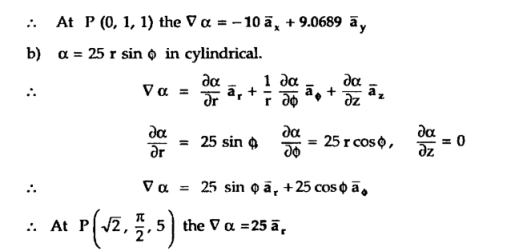

Q13) Define electric field intensity and also derive its expression?
A13) Consider a point charge Q1 as shown in figure:
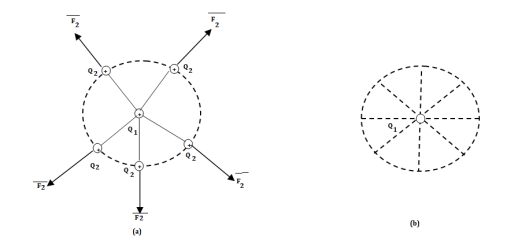
Fig. Electric Field Intensity
If any other similar charge Q2 is brought near it Q2 experiences a force. Infact if Q2 is moved around Q1 still Q2 experiences a force as shown in figure.
Thus there exists a region around a charge in which it exerts force on any other charge. This region where a particular charge exerts a force on any other chrge located in that region called electric field of that charge . The electric field of Q1 is shown in figure (b).
The force experienced by the charge Q2 due to Q1 is given by Coulombs law as ,
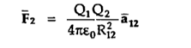
Thus, force per unit charge can be written as:

This force exerted per unit charge is called electric field intensity or electric field strength. It is a vector quantity and is directed along a segment from the charge Q1 to the position of any other charge.
It is denoted as  .
.
Another definition of electric field is the force experienced by a unit positive test charge that is Q2 = 1C.
Consider a charge Q1 as shown in figure below. The unit positive charge Q2=1C is placed at distance R from Q1. Then the force acting on Q2 due to Q1 is along the unit vector  As the charge Q2 is unit charge the force exerted on Q2 is nothing but electric field intensity
As the charge Q2 is unit charge the force exerted on Q2 is nothing but electric field intensity 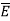 of Q1. Then the force acting on Q2 due to Q1 is along the unit vector
of Q1. Then the force acting on Q2 due to Q1 is along the unit vector 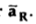 As the charge Q2 is unit charge the force exerted onQ2 is nothing but electric field intensity
As the charge Q2 is unit charge the force exerted onQ2 is nothing but electric field intensity 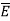 of Q1 at a point where unit charge is placed.
of Q1 at a point where unit charge is placed.
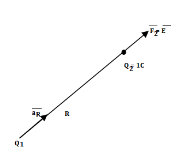
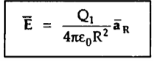
If a charge Q1 is located at the centre of the spherical coordinate system then unit vector 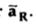 in equation (3) becomes the radial unit vector
in equation (3) becomes the radial unit vector 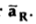 coming radially outwards from Q1 and the distance R is the radius of the sphere r.
coming radially outwards from Q1 and the distance R is the radius of the sphere r.
Q14) Define curl of a vector derive expression?
A14) The circulation of a vector field around closed path is given by curl of vector. Mathematically it is defined as
Curl of 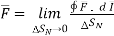
Where 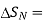 Area enclosed by the line integral in normal direction
Area enclosed by the line integral in normal direction
Thus, maximum circulation of 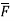 per unit area tends to zero whose direction is normal to the surface is called curl of
per unit area tends to zero whose direction is normal to the surface is called curl of 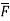 .
.
Symbolically it is represented as 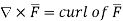
In various co-ordinate system, the curl of 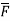 is given by,
is given by,
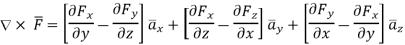
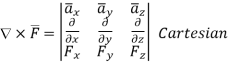 (3)
(3)
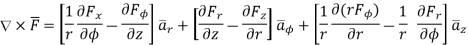
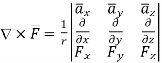 Cylindrical
Cylindrical
In 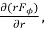 r cannot be taken outside as differential is with respect to
r cannot be taken outside as differential is with respect to
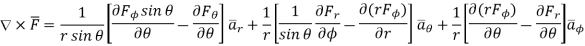
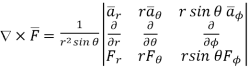 Spherical
Spherical
Q15) Define divergence and explain what id divergence of a vector?
A15) 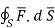 gives the flux flowing across surface S. Then mathematically divergence is defined as the net outward flow of the flux per unit volume over a closed incremental surface. It is denoted as div
gives the flux flowing across surface S. Then mathematically divergence is defined as the net outward flow of the flux per unit volume over a closed incremental surface. It is denoted as div 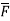 given by
given by
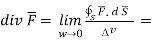 Divergence of
Divergence of 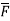
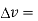 Differential volume element
Differential volume element
Symbolically it is denoted as,
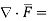 Divergence of
Divergence of 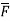
Where =Vector operator =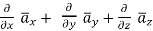
But 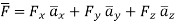
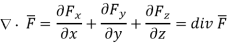
This is divergence of  in Cartesian system.
in Cartesian system.
Similarly, divergence in other co-ordinate systems are,
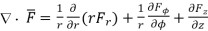 cylindrical
cylindrical
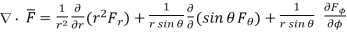 spherical
spherical
Physically divergence at a point indicate how much that vector field diverges from that point.
Consider a sloenoid that is the elctromagnet obtained by winding a coil around the core. When current passes through it flux produced around it. Such a flux completes a closed path through the solenoid hence solenoid field does not diverge. Therefore the vector field having its divergence zero is called solenoidal field.
 for
for  to be solenoidal
to be solenoidal
Q16) Write the expressions for line, surface and volume integral?
A16) Line Integrals
It is defined as any integral which is to be determined along a curve. Line integral can be defined in terms of limits of sum as are the integrals of ordinary calculus.
Above mentioned are some examples of line integrals calculated from point a to point b. In first case each element of length dl on the curve is multiplied by the local value A scalarly and then these products are summed to get the value of the integral.
Line integral in terms of cartesian coordinate can be represented as

Surface Integrals

Fig. A two sided surface
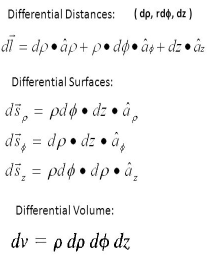
Volume Integrals
If a closed surface in space enclosing a volume V is considered then the integrals
Are the examples of volume integrals. Since volume is a three-dimensional quantity and hence three integrals.