Unit - 3
Convolution
Q1) What is convolution sum?
A1)
Using linear property of the system the interchange operator T with the summation k to obtain
y(n) = [ 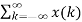 T δ(n-k)] ----------------------------------------------(4)
T δ(n-k)] ----------------------------------------------(4)
The response to the shifted impulses is represented as h(n,k)
h(n,k) = T[ δ(n-k)]
Now
y(n) = 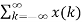 h(n,k) -----------------------------------------------------------(5)
h(n,k) -----------------------------------------------------------(5)
For time-invariant system
h(n,k) =h(n-k) ----------------------------------------------------------------------(6)
Substituting (6) in (5) we get
y(n) = 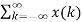 h(n-k) ------------------------------------------------------------------(7)
h(n-k) ------------------------------------------------------------------(7)
Thus, the output of the LTI system is given by the weighted sum of time-shifted responses.
The sum in eq(7) is termed as convolution sum which is given by
y(n) = x(n) * h(n) -----------------------------------------------------------------------------(8)
* denotes convolution operation.
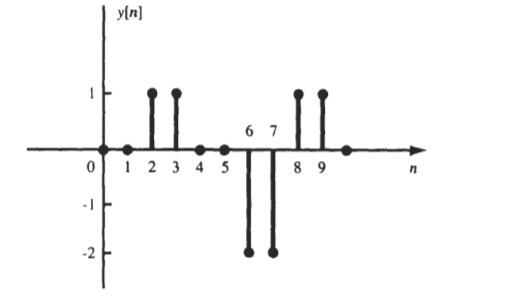
Q2) The impulse response h[n] of a discrete-time LTI system. Determine and sketch the output y[n] of this system to the input x[n]
A2)
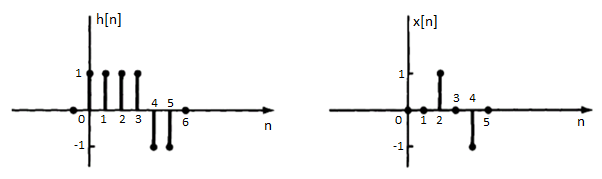
h[n] = δ[n] + δ[n-1] + δ[n-2]+ δ[n-3]+ δ[n-4]+ δ[n-5]
x[n] = δ[n-2] - δ[n-4]
x[n] * h[n] = x[n] * { δ[n] + δ[n-1] + δ[n-2]+ δ[n-3]+ δ[n-4]+ δ[n-5]}
= x[n] + x[n-1] + x[n-2]+ x[n-3]+ x[n-4]+ x[n-5]
y[n] = δ[n-2]- δ[n-4]+ δ[n-3]- δ[n-5] + δ[n-4]- δ[n-6]+ δ[n-5]- δ[n-7] - δ[n-6]+ δ[n-8]- δ[n-7]+ δ[n-9]}
= δ[n-2]+ δ[n-3]-2 δ[n-6]-2 δ[n-7] + δ[n-8]+ δ[n-9]
y[n] = {0,0,1,1,0,0,-2,-2,1,1}
Q3) What is convolution integral?
A3)
Consider an LTI system which is initially related at t=0. If the input of the system is an impulse, then the output of the system is denoted by h(t) is called the impulse response of the system.
We can denote
h(t) = T [ δ(t)]
We know that any arbitrary signal x(t) can be represented as
x(t) = 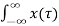
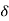 ( t-
( t-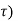 d
d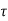 ------------------------------------------------------(1)
------------------------------------------------------(1)
The system output is given by
y(t) = T[x(t)] --------------------------------------------------------------------------------(2)
Substituting (1) in (2)
y(t) = T [ 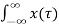
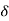 ( t-
( t-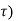 d
d --------------------------------------------------------(3)
--------------------------------------------------------(3)
For linear system
y(t) = [ 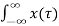 T[
T[ 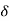 ( t-
( t-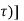 d
d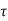 --------------------------------------------(4)
--------------------------------------------(4)
If the response of the system due to impulse δ(t) is h(t) then the response of the system due to delayed impulse is
h(t,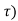 = T [ δ(t-T)] --------------------------------------------------------------(5)
= T [ δ(t-T)] --------------------------------------------------------------(5)
Substituting (5) in (4) we get
y(t) = [ 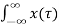 h(t,τ) dτ -------------------------------------------------------(6)
h(t,τ) dτ -------------------------------------------------------(6)
For a time invariant system the output due to the delayed input by T is equal to delayed output by T, That is
h(t,τ) = h(t-τ) ---------------------------------------------------------------(7)
Substituting (7) in (6) we get
y(t) = 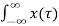 h(t-τ) dτ -----------------------------------------------------------(8)
h(t-τ) dτ -----------------------------------------------------------(8)
This is called convolution Integral. The convolution of two signal x(t) and h(t) can be represented as
y(t) = x(t) * h(t)
Q4) Compute convolution integral by convolution method?
A4)
The procedure is as follows:
- For the given signals x(t) and h(t) graph the signals x(τ) and h(τ) as a function of independent variable τ.
- Obtain the signal h(t-τ) by folding h(τ) about τ=0 and then time shifting by time t.
- Graph both signals x(τ) and h(t-τ) on the same τ-axis beginning with very large negative time shift t.
- Multiply the two signals x(τ) h(t-τ) and integrate over the overlapping interval of two signals to obtain y(t)
- Increase the time shift and take the new interval whenever the function of either x(τ) and h(t-τ) changes. The value of t at which the change occurs defines the end of the current interval and beginning of a new interval. Calculate y(t) using step 4.
- Repeat steps 5 and 4 for all intervals.
Q5) Find the convolution of x(t) and h(t) for
x(t) =1 0 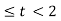
= 0 otherwise
A5)
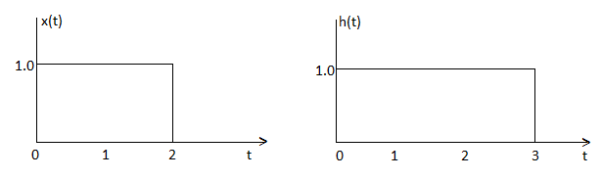
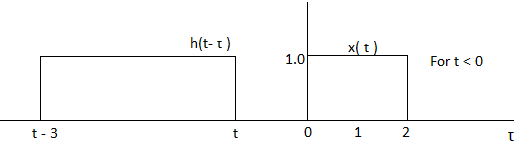
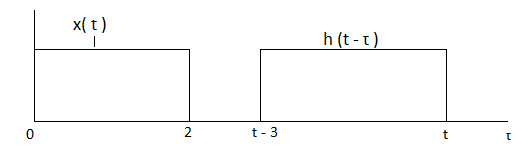
As shown in Figure the signals x(τ) and h(t-τ) does not overlap for t<0. Therefore the product x(τ) h(t-τ) is zero.
That is,
y(t) = 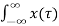 h(t-τ) =0 for t<0
h(t-τ) =0 for t<0
Now the shift the signal h(t-τ) right until the right edge of the signal h(t-τ) intersects left edge of x(τ).
In the interval 0 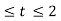
y(t) = 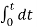 = t
= t
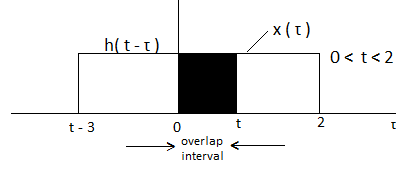
In the interval 2 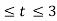
y(t) = 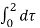 = 2
= 2
In the interval 3 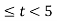
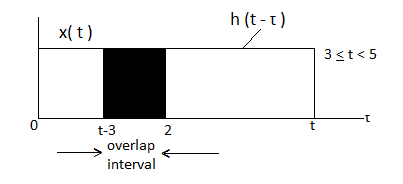
y(t) = 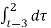 = 2 – (t-3)
= 2 – (t-3)
= 5-t.
For t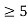
The signals x(τ) and h(t-τ) do not overlap. Therefore y(t)=0.
y(t) = 0 for t<0
= t for 1 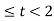
= 2 for 2 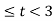
= 5-t for 3 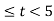
=0 for t 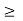 5.
5.
The sketch y(t) is as shown in figure
Q6) Find the convolution of Unit Step to Exponential.
A6)
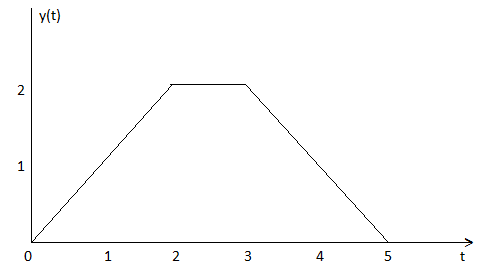
Given:
x(t) = e -2 u(t) h(t) = u(t+2)
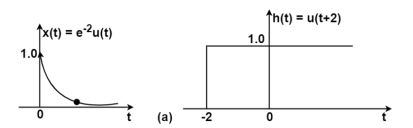
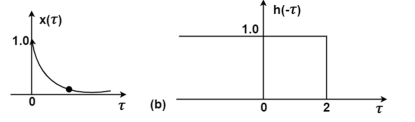
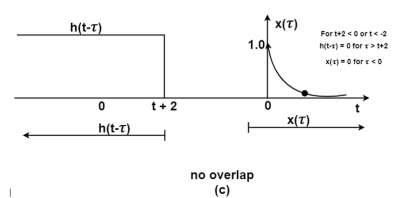
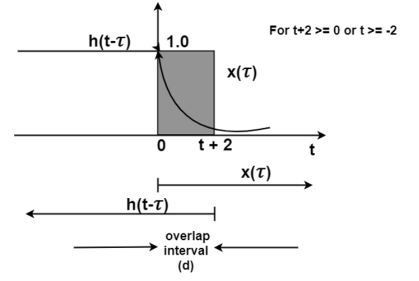
Figure (a) shows x(t) and h(t). Fig (b) shows x(τ) and h(-τ) as functions of τ. The function h(-τ) can be obtained by folding the signal h(τ) about τ=0.
Figure (c ) shows that signal h(t-τ) is sketched for t<-2 by shifting h(τ) to left. For t<-2 x(τ) and h(t-τ) does not overlap and the product x(τ) h(t-τ) =0 that is
y(t) =0 for t<-2
Now increase the time shift until the signal h(t-τ) intersects x(τ). Figure (d) shows the situation for t>-2.
Here x(τ) =0 for τ <0 and h(t-τ) does not overlap and the product x(τ) h(t-τ) =0 that is
y(t)=0 for t<-2
Now increase the time shift t until the signal h(t-τ) intersects x(τ).
Figure (d) shows the situation for t>-2. Here x(τ) and h(t-τ) overlapped. But x(τ) =0 for τ<0 and h(t-τ) = 0 for τ > t+2. Therefore, the integration interval is from τ=0 to τ=t+2
y(t) = 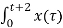 h(t-τ) dτ
h(t-τ) dτ
= = 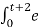 -2τ dτ
-2τ dτ
= -1/2 e -2 τ | 0 t+2
= -1/2 [ e -2 (t+2) -1]
= 1 – e -2(t+2) /2
y(t) = 0 for t<-2
= 1 – e-2(t+2)/2 for t 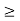 -2
-2
Q7) Find the convolution of exponential to exponential
x(t) = e -|t|
h(t) = e -2(t+1) u(t+1)
A7)
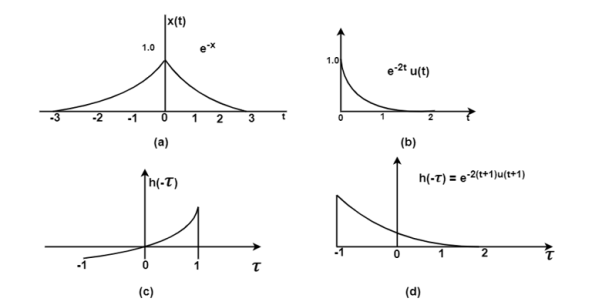
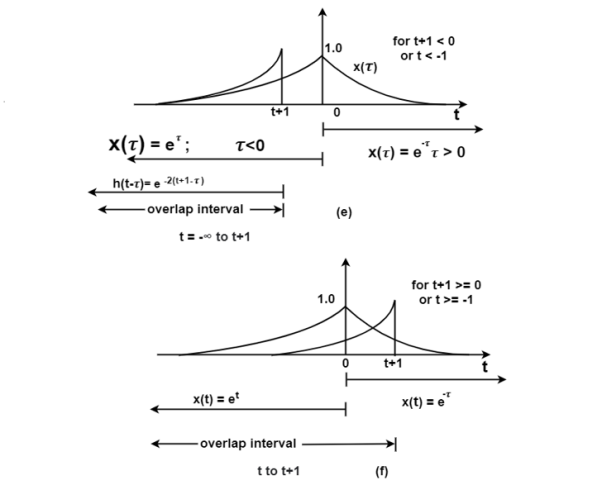
Fig (a) shows the signal x(t). In fig(b) the signal e -2t u(t) is sketched from which can be obtained from the signal h(t) = e -2(t+1) u(t+1)
Fig ( c ) shows the signal h(-τ) which can be obtained by folding the signal h(τ) about t=0.
In fig (e ) the signals x(τ) and h(t-τ) are drawn on the same axis.
For (t+1) <0 or t<-1 the signals x(τ) and h(t-τ) overlap over the interval -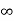
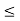 τ
τ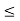 t+1.
t+1.
During this interval the signal x(τ) = e τ and h(t-τ) = e -2 (t+1-τ). Therefore, for
t<-1
y(t) = 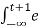 τ e -2(t+1-τ) dτ
τ e -2(t+1-τ) dτ
= e -2t -2 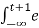 3 τ dτ
3 τ dτ
= e -2(t+1) /3 e 3 τ | - 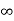 0 + e -2 (t+1) e τ | 0 t+1
0 + e -2 (t+1) e τ | 0 t+1
= e -2(t+1) /3 [1] + e –2(t+1) [ e t+1 -1 ]
= e -2(t+1) /3 + e –(t+1) – e -2 (t+1)
= e –(t+1) – 2/3 e -2(t+1)
y (t) = 1/3 e t+1 for t<-1
= e –(t+1) – 2/3 e -2(t+1) for t 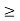 -1
-1
Q8) Explain the computation of convolution sum?
A8)
For x(n) = {3,2,-1,2,4,1} find the sum of the shifted unit impulses.
A8. Given x(n) = {3,2,-1,2,4,1}
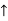
-1,0,1,2,3,4
x(-1) = 3. x(0)=2 , x(1)=-1, x(2) =2, x(3)=4,x(4) =1
x(n) = 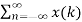 δ(n-k)
δ(n-k)
x(-1) δ(n+1) + x(0) δ(n) + x(1) δ(n-1) + x(2) δ(n-2)+ x(3) δ(n-3)+ x(4) δ(n-4)
We get
3 δ(n+1) + 2 δ(n) - δ(n-1) + 2 δ(n-2)+ 4 δ(n-3)+ δ(n-4)
Q9) Find the properties of convolution sum?
Commutative Property
The commutative property states that the order in which two sequences are convolved is not important. Mathematically, the commutative property is
x(n) * h(n) = h(n) * x(n)
From a systems point of view, this property states that a system with a unit sample response h(n) and input x(n) behaves in exactly the same way as a system with unit sample response x(n) and an input h(n).
This is illustrated in Fig. (a).
Associative Property
The convolution operator satisfies the associative property, which is
[x(n) * h1(n) } * h2(n) = x(n) * { h1(n) * h2(n)}
From a systems point of view, the associative property states that if two systems with unit sample responses h1(n) and h2(n) are connected in cascade as shown in Fig. (b), an equivalent system is one that has a unit sample response equal to the convolution of h1 (n) and h2(n):
Heq = h1(n) * h2(n)
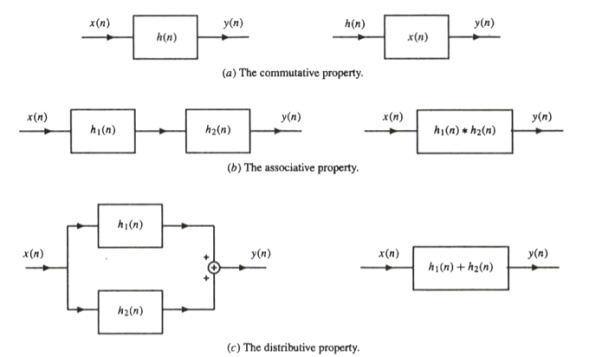
Distributive Property
The distributive property of the convolution operator states that
x(n) * {hl(n) + h2(n)} = x(n) * hJ(n) + x(n) * h2(n)
From a systems point of view, this property asserts that if two systems with unit sample responses h J (n) and h2(n) are connected in parallel, as illustrated in Fig. (c), an equivalent system is one that has a unit sample response equal to the sum of hJ(n) and h2(n):
Heq (n) = h1(n) + h2(n)
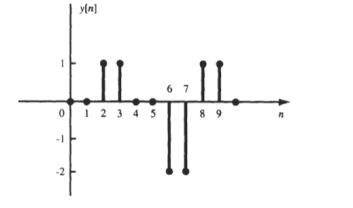
Q10) The impulse response h[n] of a discrete-time LTI system. Determine and sketch the output y[n] of this system to the input x[n]
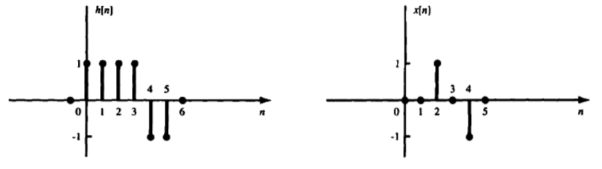
A10)
h[n] = δ[n] + δ[n-1] + δ[n-2]+ δ[n-3]+ δ[n-4]+ δ[n-5]
x[n] = δ[n-2] - δ[n-4]
x[n] * h[n] = x[n] * { δ[n] + δ[n-1] + δ[n-2]+ δ[n-3]+ δ[n-4]+ δ[n-5]}
= x[n] + x[n-1] + x[n-2]+ x[n-3]+ x[n-4]+ x[n-5]
y[n] = δ[n-2]- δ[n-4]+ δ[n-3]- δ[n-5] + δ[n-4]- δ[n-6]+ δ[n-5]- δ[n-7] - δ[n-6]+ δ[n-8]- δ[n-7]+ δ[n-9]}
= δ[n-2]+ δ[n-3]-2 δ[n-6]-2 δ[n-7] + δ[n-8]+ δ[n-9]
y[n] = {0,0,1,1,0,0,-2,-2,1,1}
Q11) For x(n) = {3,2,-1,2,4,1} find the sum of the shifted unit impulses.
A11)

x(-1) = 3. x(0)=2 , x(1)=-1, x(2) =2, x(3)=4,x(4) =1
x(n) = 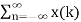 δ(n-k)
δ(n-k)
x(-1) δ(n+1) + x(0) δ(n) + x(1) δ(n-1) + x(2) δ(n-2)+ x(3) δ(n-3)+ x(4) δ(n-4)
We get
3 δ(n+1) + 2 δ(n) - δ(n-1) + 2 δ(n-2)+ 4 δ(n-3)+ δ(n-4)
Q12) Find the response of the system y(t) of an LTI system whose x(t) and h(t) are as shown in the figure.
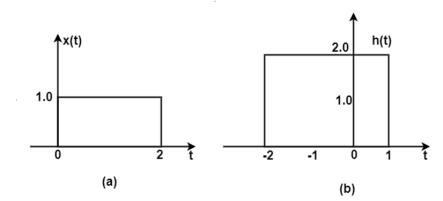
Fig. x(t) and h(t) signals
A12)
The figure shows the signal x(τ) and h(-τ). In the figure, the signals x(τ) and h(t-τ) do not overlap. Therefore, the product x(τ) h(t-τ) is equal to zero. For t<-2 the signals x(τ) and h(t-τ) does not overlap. Therefore, the product x(τ) h(t-τ) is equal to zero.
Hence
y(t) = 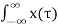 h(t-τ) dτ
h(t-τ) dτ
= 0 for t<-2
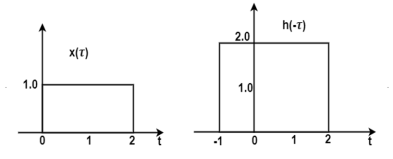
Fig. Convolution of x(t) and h(-τ)
Now increase the value of t and shift the signal h(t-τ) as shown in figure. Here the overlap interval is τ = 0 to t+2 . In this interval x(τ) = 1.0 ; h(t-τ) = 2.0
Figure. Convolution of x(τ) h(t-τ)
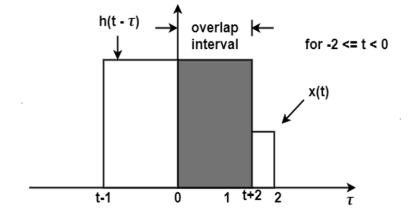
Figure. Output of the convolution x(t) and h(t)
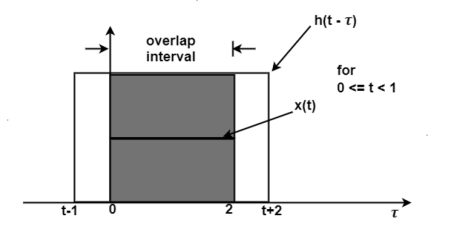
Figure. Output for t<1
Therefore,
y(t) = 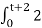 d τ
d τ
= 2τ | 0 t+2 = 2(t+2) = 2t + 4
This value holds for -2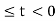
In the interval 0 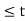
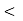 1 the overlap interval is constant that is from τ=0 to τ=2
1 the overlap interval is constant that is from τ=0 to τ=2
Therefore
y(t) = 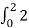 d τ =2 τ | 0 2 =4
d τ =2 τ | 0 2 =4
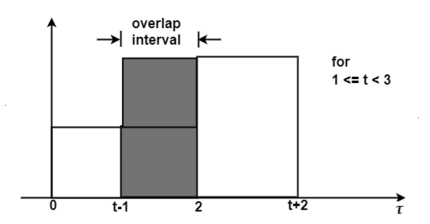
Figure. Output waveform for t<3
If we shift h(t-τ) further the resultant diagram is shown in fig 4.29. Here the overlap interval is from τ = t-1 to τ=2. Therefore, for the interval 1 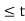
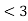
y(t) = 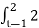 dτ
dτ
= 2τ | 2 t-1
= 2[ 2 – (t-1)]
= 6 – 2t
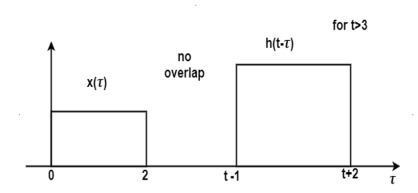
Figure. Output waveform for t>3
For t>3 the signals do not overlap. Therefore
y(t) = 0 for t>3
y(t) = 0 for t 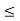 -2
-2
= 2t + 4 for -2  <0
<0
= 4 for 0 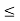 t <1
t <1
= 6 -2t for 1 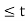 <3
<3
=0 for t 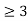
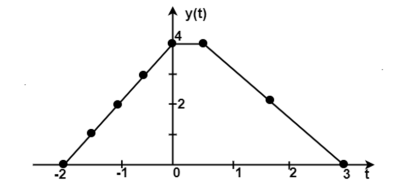
Figure. Final output waveform