Unit - 4

Time and Frequency Domain Transformations

Q1) Explain the Fourier series Representation of periodic signals?

A1) A signal is said to be periodic if it satisfies the condition x (t) = x (t + T) or x (n) = x (n + N).

Where T = fundamental time period,

ω0= fundamental frequency = 2π/T

There are two basic periodic signals:

x(t) = cos wot (sinusoidal)

x(t) = e jwot (complex exponential)

These two signals are periodic with period T=2π/ω0

A set of harmonically related complex exponentials can be represented as ɸk(t)

ɸk(t) = { e jkwot} = { e jk(2π/T)t} where k=0,±1,±2,±3,………………(1)

All these signals are periodic with period T.

According to orthogonal signal space approximation of a function f(x) with n mutually orthogonal functions is given by

x(t) = 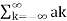  e jkwot ……………………………………………….(2)

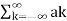= k ejkwot

Where ak= Fourier coefficient = coefficient of approximation.

This signal x(t) is also periodic with period T.

Equation 2 represents Fourier series representation of periodic signal x(t).

The term k = 0 is constant.

The term k=±1 having fundamental frequency ω0, is called as 1st harmonics.

The term k=±2 having fundamental frequency 2ω0, is called as 2nd harmonics, and so on...

The term k=±n having fundamental frequency nω0, is called as nth harmonics.

Q2) Write a short note on waveform symmetries?

A2)

• Even function symmetry

A function is defined to be even if and only if

f(t) = f(-t) -------------------------------------------------------------(1)

If the condition is satisfied then eq(1) is said to be even because polynomial functions with even components 

For any even periodic functions, the equations for the Fourier coefficients

Av = 2/T 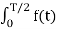dt ---------------------------------------------------(2)

Ak = 4/T 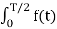coskwot dt --------------------------------------------(3)

Bk=0 for all k --------------------------------------------------(4)

In eq(4) all b co-effecients are zero if the function is even. The figure depicts the even periodic function.

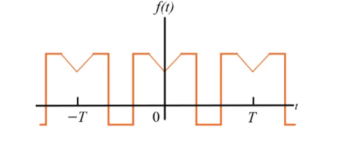
Figure. Even symmetry

Av = 1/T 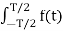  dt

= 1/T   dt +

• Odd function symmetry

A periodic function is defined to be odd if

f(t) = -f(t) ---------------------------------(1)

The function that satisfies eq(1) is said to be odd because polynomial funtions with odd exponents. The expression for Fourier co-effecients are:

Av=0

Ak=0 for all k;

Bk = 4T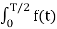 sinkwo dt ---------------------------------(2) 

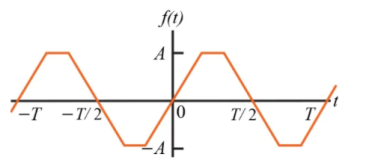
Figure. Odd function symmetry

• Half Wave Symmetry

A function is said to have half-wave symmetry if it satisfies the following constraint:

f(t) = -f(t - T/2)   ------------------------------------   (1)

Equation 1 expresses that a periodic function has a half-wave symmetry if, after it has been shifted by one-half of a period and inverted, it is said to be identical to the original periodic function.

For instance, the periodic functions illustrated in Figures possess half-wave symmetry.                      

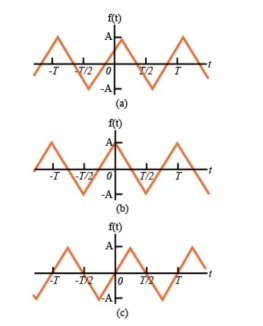
Figure. Half wave Symmetry

• Quarter Wave Symmetry

If a function has half-wave symmetry and symmetry about the midpoint of the positive and negative half-cycles, the periodic function is said to have quarter--wave symmetry. This function is illustrated in Figure

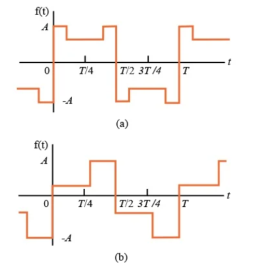
Figure. Quarter Wave Symmetry

Q3) Explain the calculation of Fourier co-efficient?

A3) We know that x(t) = 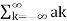   e jkwot ------------------------(1)

Multiply e-jnwot on both sides we get

x(t) e -jnwot = 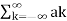e jkwot  . e- jnwot  

Consider integral on both sides we get

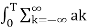e jkwot dt =   e jkwot   . e- jnwot  

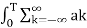=   e j(k-n)wot  dt  

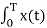= e jkwot dt = 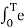j(k-n)wot dt  --------------------------(2)

By Eulers formula

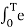j(k-n)wot dt = 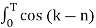wo  dt  + j 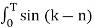wo  dt 

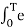j(k-n)wot dt =  { T      k=n

0        k 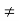n

Hence in equation(2) the integral is zero for all values of k except at k=n. Put k=n is equation 2

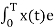= j(k-n)wot dt = anT

=an = 1/T 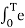-jnwot

Replace n by k we get

= ak = 1/T 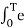-jkwot  dt

x(t) =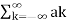  e j(k-n) wot

Where ak = 1/T 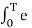-jkwot dt

Q4) Derive Fourier Transform?

A4) The (CT) Fourier transform (or spectrum) of x(t) is

X(jw) = 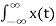  e -jwt    dt ---------------------------------------(1)

x(t) can be reconstructed from its spectrum using the inverse Fourier transform

x(t) = 1/ 2 π    e jwt    dw    ------------------------------------------(2)

The above two equations are referred as Fourier transform pair with the first one being the analysis equation and the second being the synthesis equation.

Notation

X(jw) = F{x(t)}

x(t) = F -1 {X(jw)}

x(t) and X(jw) form a Fourier transform pair denoted by

Q5) Explain convolution?

A5) Imagine we have a function f[t] whose Fourier transform is F[w] and another function g[t] whose transform is G[w]. Then the convolution is

f[t] * g[t] = 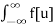g[t-u] du

We write g[t-u] in terms of Inverse Fourier transform

g[t-u] =   1/2π 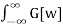 E Iw(t-u) dw dw

Thus

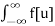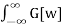f[t] * g[t] = 1/2π E Iw(t-u) dw dw du

= 1/2π 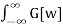  E Iwt 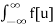 E -Iwu du dw

But the right hand integral above is the Fourier transform of f[u] so

f[t] * g[t] = 1/2π 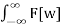 G[w] E -Iwu dw

The convolution property states that:

x(t) * h(t) > X(w) H(w)

Let

y(t) = 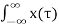h(t-τ) dτ = x(t) * h(t)

Y(w) = 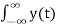e -jwt dt = 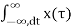h(t-τ) dτ e -jwt dt

If we switch the order of the two integrals we get

Y(w) = 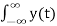e -jwt dt =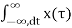       h(t-τ) dτ e -jwt dt    let u=t-τ

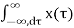
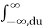=       h(u)  e -jw(u+τ) du dτ

=   e -jwτ dτ 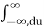   h(u)  e -jwu du

= X(w) H(w)

Therefore,

y(t) = x(t) * h(t) <-> Y(w) = X(w) H(w)

Fourier Transform of the convolution of two functions is simply the product of the Fourier Transforms of the functions.

Q6) Explain the magnitude and phase response?

A6) H(e jw) = H R ( e jw) + j H I ( e jw) = | H ( e jw) | e j 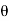1 (w)

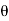1 (w) = angle H(e jw)

Example:

h[n] = - δ[n]

    | H (ejw)| = 1    angle H(e jw)  = π

In the magnitude or phase representation a real valued frequency response does not mean that the system is zero-phase.

Using this representation,

|Y (e jw) | = | H ( ejw)| | X (ejw)|

Thus, |H(ejω)| and angle H(ejω) are commonly referred to as the gain and the phase shift of the system, respectively.

In magnitude and phase plots, as ω goes through a zero on the unit circle, the magnitude will go to zero and the phase will flip by π, as shown in the figure below.

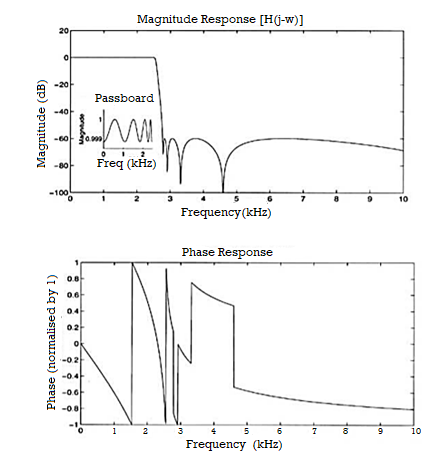
Figure. Magnitude and Phase response

Q7) Explain DTFT?

A7) The discrete-time Fourier transform (DTFT) or the Fourier transform of a discrete–time sequence x[n] is a representation of the sequence in terms of the complex exponential sequence ejωn.

The DTFT sequence x[n] is given by

X(w) =   e-jwn ---------------(1)

Here X(w) is a complex function of real frequency variable w and can be written as

X(w) = Xre (w) + j X img(w)

Where  Xre (w) , j X img(w) are real and Imaginary parts of X(w)

Xre(w) = |X(w)| cos 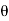(w)

Ximg(w) = |X(w)| sin 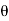(w)

|X(w)| 2 = |Xre(w)| 2 + |Xim(w)| 2

And | X(w)|   can be represented as

X(w) = |X(w)| e j(w)

Inverse Discrete Fourier Transform is given by

x(n) = 1/2π 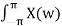e jwn dw

Q8) Find the DFT of the sequence f(n) ={ 8,4,8,0}

A8) F[n] = 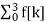  e -j π/2 nk =  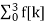 (-j) nk

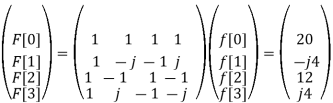
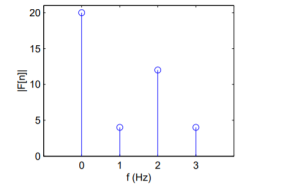
Figure. Magnitude of the four point sequence.

Q9) Explain Parseval’s theorem?

A9) Consider two periodic signals x1(t) and x2(t) with equal period T. If the Fourier series co-efficient of these two signals are cn and dn then

1/T    x2(t)   =  1/T 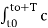n  e j n Ωot [  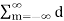 m e jmΩot  ]    dt---------------------(1)

= 1/T 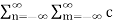    n d *m           e j(n-m)Ωot  dt ------------------------------(2)

= 0     n≠ m

= n d *n   n=m --------------------------------(3)

If x1(t) = x2(t) = x(t) then eq(3) becomes

1/T 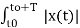    2 = 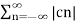  2     --------------------------------(4)

The above equation can be written as

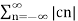  2     = c0 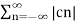2 +   2    

n≠0      

= c0 2 + 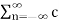 n c *n     

n≠0 

a0 2 + 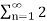[Re(c 2 n ) + Im (cn ) 2]

= a0 2 + 2 n /2 + b 2 n /2

Q10) Find H(z), poles and zeros for the difference equation given by

y[n] – 3/8 y[n-1] – 7/16 y[n-2] = x[n] + x[n-2]

A10)

Here ao=1,a1=-3/8,a2=-7/6,bo=1,b1=0,b2=1

H[z] = 1 + z -2 / 1 -3/8 z-1 -7/16 z -2

= (1+j z-1 ) (1 -jz-1)  / (1-7/8 z-1) ( 1+1/2 z-1)

Zeros : z=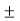j represented by o.

Poles z= 7/8 , z=-1/2  represented by x.

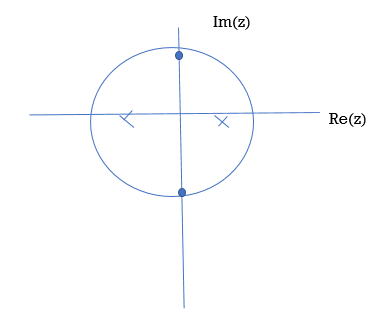
Fig. Poles and Zeros