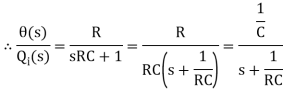Unit - 1
Introduction to need for automation and automatic control
Q1) Find SFG for the block diagram below?
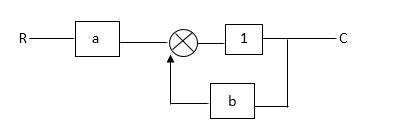
A1)
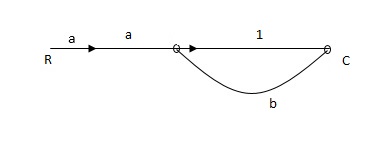
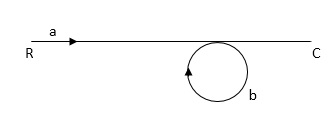
Ra+cb =c
c/R= a/1-b
Q2) The SFG shown has forward path and singles isolated loop determine overall transmittance relating X3 and X1?
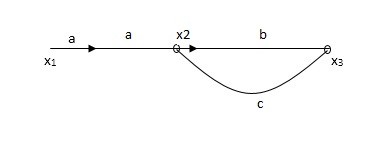
A2)
X1- I/p node
X2-Intenmediale node
X3- o/p node
Ab- forward path (p)
Bc- 1 loop (L)
At node XQ:
X2 = x1a + x3c [Add i/p signals at node]
At node x3:
x2b =x3
(x1a+x3c) b = x3
X1ab = x3 (1-bc)
X1 = x3 (1-bc)/ab
Ab/(1-bc) = x3/x1
T= p/1-L

X1:- I/p node x2, x3,x4,x5,Qnlexmedili node
X0:- o/p node abdeg:- forward path
Bc, ef :- Loop [isolated]
x2 = ax1+c x3
x3= bx2
x4 = d x3+f x5
x5 = e x4
x6= g x5
x6 = g(e x4) = ge [dx3+ e f x5]
xb = ge [d (bx2) + f (e x4)]
xb = ge [ db (ax1+cx3) + fe (dx3+ fx5)]
xb = ge [db (ax1+cb (ax1+x3) +fe[cdbx2]+
f( e [db (ax1+ cx3)
x2 = ax1 + cb (x2) x4 = d bx2 + f exq
x2 = ax1 + cbx2 = db (d4) + fe/1-cb
x2 = ax1/(1-cb) xy = db x2 + f x6/g
xy = db [ax1]/1-cb + f xb/g
x5 = c db ( ax1)/1-cb + efxb/g
xb = gx5
= gedb (ax1)/1-cb + g efxb/g
Xb = gx5
Gedb (ax1)/1-cb + g efxb/g
(1-gef/g) xb = gedb ax1/1-ab
Xb/x1 = gedb a/ (1- ef – bc + beef
Xb/x1 = p/ 1- (L1+L2) + L1 L2for isolated loops
Q3) Reduce given B.D to canonical (simple form) and hence obtain the equivalent Tf = c(s)/ R(S)?
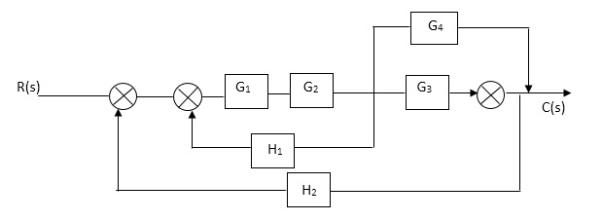
A3)
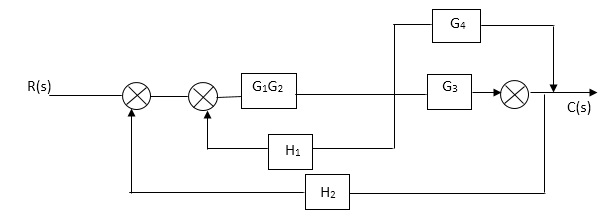
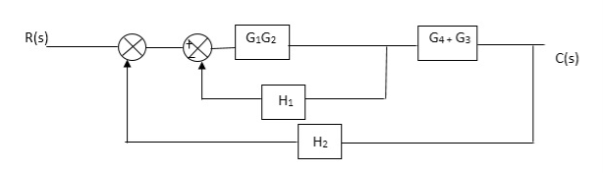
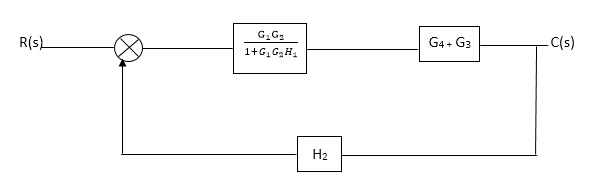
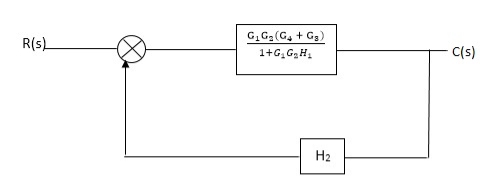
Fig. Final reduced block diagram
C(S)/R(S) = (G1G2) (G3+G4)/1+G1G2H1)/1-G1,G2(G3+G4) H2/1+G1G2H1
= G1G2(G3+G4)/1+G1G2H1-G1G2H2(G3+G4)
=G1G2(G3+G4)/1+(H1-H2)(G1G2) (G3+G4)
C(s)/R(S) = G1G2(G3+G4)/1+(H1-H2(G3+G4)) G1 G2
Q4) Reduce using Masons gain formula
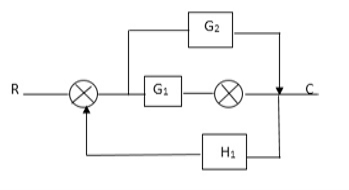
A4)
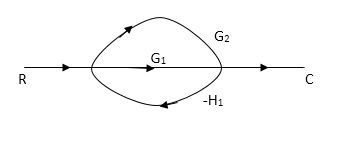
P1= G1 p2 =G2 Delta1 =1
L1= -G1 H1
 = 1-(-G1H1)
= 1-(-G1H1)
= 1+G1H1
T= G1+G2/1+G1H1
Q5) Determine overall gain reliably x5 and x1 Draw SFG
X2 = ax1+ f x2
X3= bx2 +exy
X4 = cx3+hx5
X5 =dx4 + gx2
A5)
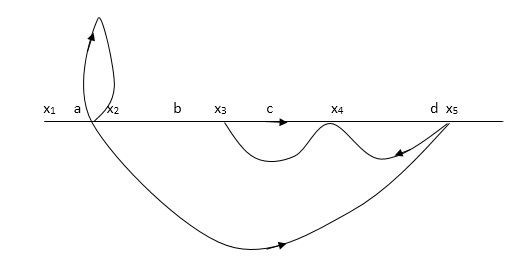
P1 = abcd p2 = ag
L1 = f L2 = ce, L3= dh
 1 = 1
1 = 1
 2= 1-ce
2= 1-ce
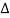 = 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[f+ le = dh] + [fce +fdh]
T= abcd+ ag (1-ce)/1-[ftce + dh ] + (fce + fdh)
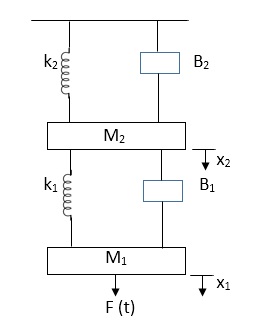
Q6) Draw the free body diagram and write the differential equation for system below.
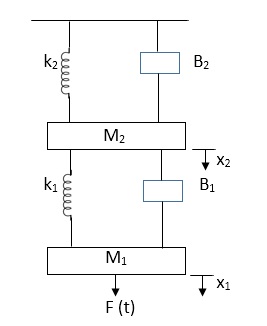
A6)
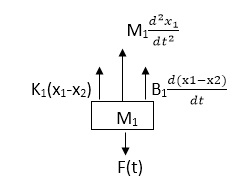
The free body diagram for M1 will be
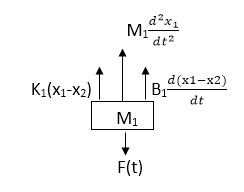
F(t) = M1 d2/dt2x1+ B1 d/dt (x1-x2)+ k1(x1-x2)
Similarly for M2we have
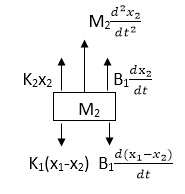
K1(x1-x2) + B1d/dt(x1-x2) = k2x2+M2d2/dt2+B2dx2/dt
Q7) For the given mechanical system below draw the analogus system (force. Voltage) & find V0(s)/V1(s)
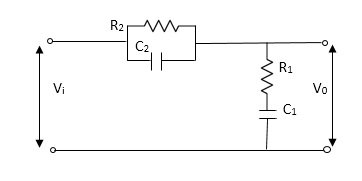
A7)
Let Z1 = R2 11 1/c2
=R2*1/c2s/R2+1/c2s
Z1= R2/1+R2c2s
Let Z2 = R1+1/c1s
Z2= 1+R1c1s/c1s
V0(s)/vi(s) = z2/z1+z2
=1+R1c1s/c1s/R2/1+R2c2s+1+R1c1s/c1s
V0(s)/v0(s) =(c1+R1c1s) (1+R2c2s)/R2c1s+1+sR1c1s2R1R2c1c2
Q8) Explain force-voltage analogy?
A8)
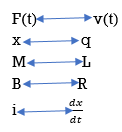
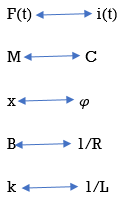
If the dynamic characteristics of an electrical system is identical to that of a mechanical system, then the electrical system is said to be analogous to the mechanical system. This can be done by comparing the mathematical models of both the systems.
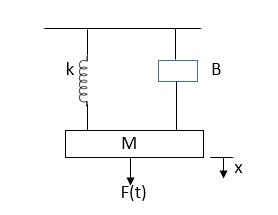
Fig. Mechanical System
The equation for above mechanical system is given by
f(t) = M 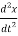 +B
+B 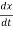 +kx (1)
+kx (1)
For series RLC circuit the mathematical equation is given as
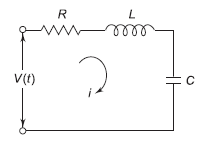
Fig. Electrical System
V(t)= Ri + L 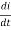 +
+ 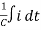
i = 
V(t) = L 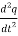 + R
+ R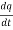 +
+  (2)
(2)
Comparing 1 and 2 we see that
Q9) Explain force-current analogy?
A9)
For parallel RLC circuit shown below the KCL equation is written as
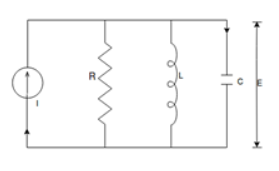
Fig. Electrical Circuit
i(t) = C  +
+  +
+ 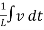
v = 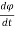
i(t) = C 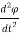 + R
+ R +
+ 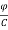 (3)
(3)
Comparing 1 and 3 we find that
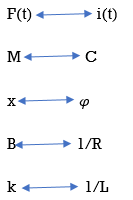
Q10) Reduce the give block diagram to find the transfer function?
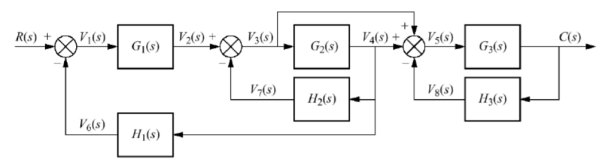
A10)
The above block diagram can be reduced as shown below
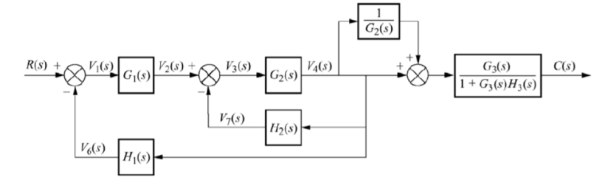
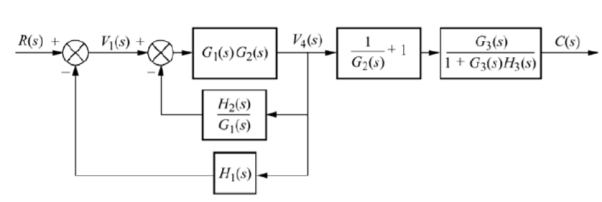
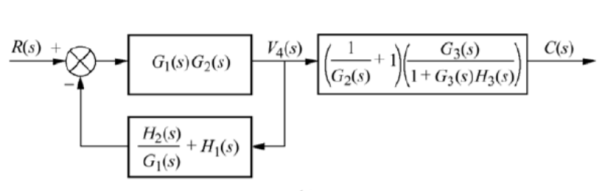


From above reduced figure the transfer function is very clear.
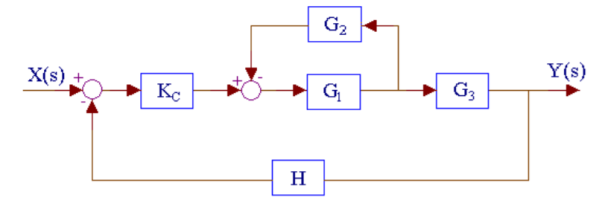
Q11) Reduce the given figure using block diagram reduction to find its transfer function?
A11)
The above system can be reduced as

Kc, (G1/1+G1G2) and G3 are in series. H is in feedback with them.
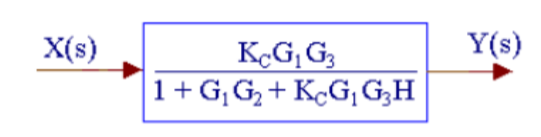
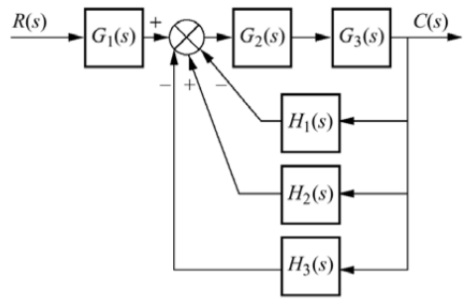
Q12) Reduce the given system using block diagram reduction technique?
A12)
The figure can be reduced as
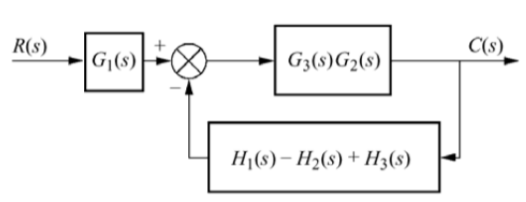
G1 and G2 are in series and H1, H2 and H3 are in parallel.
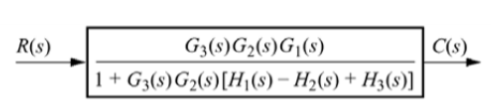
G1 is in series with feedback configuration. The transfer function becomes
C(s)/R(s) =
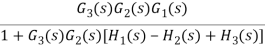
Q13) Compute the transfer function of the given figure?
A13)
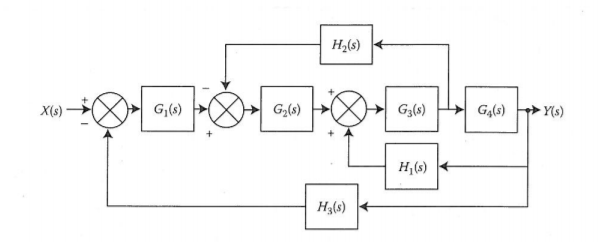
The branch point at the left of the block with transfer function G4(s) is moved at the right of G4(s). The equivalent block diagram is
The transformation is applied to blocks with transfer function G3(s), G4(s) and H1(s).
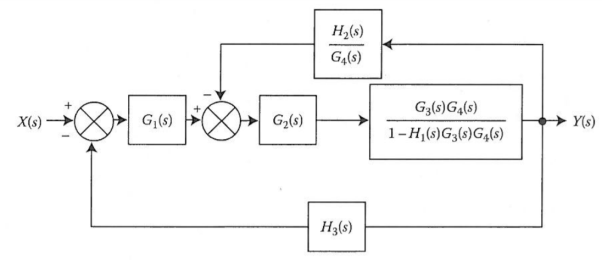
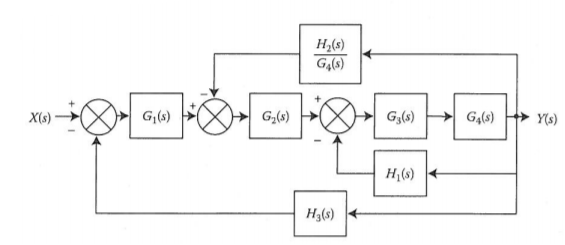
We apply transformation to the loop with TF H2(s)/G4(s) we get
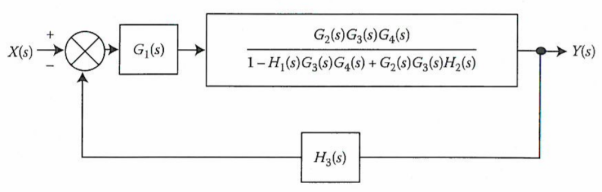
Again, applying same transformation to above figure we get the final reduced structure

Q14) Derive the transfer function of thermal system?
A14)
Thermal systems are those that involve the transfer of heat from one substance to another. The model of thermal systems is obtained by using thermal resistance and capacitance which are the basic elements of the thermal system. The thermal resistance and capacitance are distributed in nature. But for simplicity in analysis lumped parameter models are used.
Consider a simple thermal system shown in the below figure. Let us assume that the tank is insulated to eliminate heat loss to the surrounding air, there is no heat storage in the insulation and liquid in the tank is kept at uniform temperature by perfect mixing with the help of a stirrer. Thus, a single temperature is used to describe the temperature of the liquid in the tank and of the out flowing liquid. The transfer function of thermal system can be derived as shown below.

Fig. Thermal System
Let θ1 = Steady state temperature of inflowing liquid, °C
θ0 = Sandy state temperature of outflowing liquid, °C
G = Steady state liquid flow rate, Kg/sec
M = Mass of liquid in tank, Kg
c = Specific heat of liquid, Kcal/Kg °C
R = Thermal resistance, °C - sec/Kcal
C = Thermal capacitance, Kcal/°C
Q = Steady state heat input rate, Kcal/Sec
Let us assume that the temperature of inflowing liquid is kept constant. Let the heat input rate to the thermal system supplied by the heater is suddenly changed from Q to Q + q1. Due to this, the heat output flow rate will gradually change from Q to Q + q0. The temperature of the outflowing liquid will also be changed from θ0 to θ0 + θ.
For this system the equation for q0, C and R is obtained as follows,
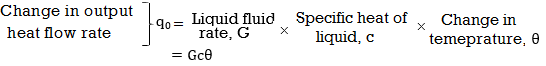
Thermal capacitance, C = Mass, M x Specific heat of liquid, c = Mc
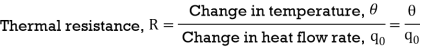
On substituting for qo from equation (1) in equation (3) we get,
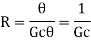
In this thermal system, rate of change of temperature is directly proportional to change in heat input rate.
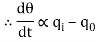
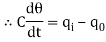
The constant of proportionality is capacitance C of the system.
Equation (5) is the differential equation governing system. Since, equation (5) is of first order equation, the system is first order system.
From equation (3), R = θ/q0
q0 = θ/R
On substituting for q0 from equation (6) in equation (5) we get,
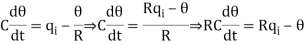
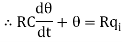
Let, L {θ} = θ(s); L{dθ/dt} = sθ(s) ; L{q1} = Q1(s)
On taking Laplace transform of equation (7)
RC s θ(s) + θ(s) = R Q1(s)
θ(s) [sRC + 1] = R Q1(s)
θ(s)/Q1(s) is the required transfer function of thermal system.

Unit - 1
Introduction to need for automation and automatic control
Q1) Find SFG for the block diagram below?
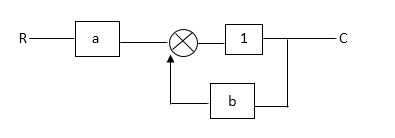
A1)
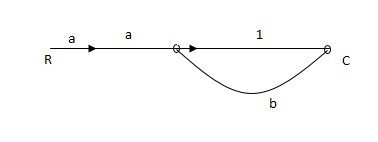
Ra+cb =c
c/R= a/1-b
Q2) The SFG shown has forward path and singles isolated loop determine overall transmittance relating X3 and X1?
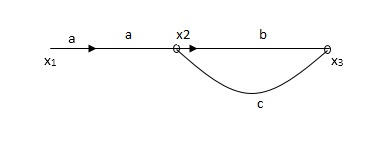
A2)
X1- I/p node
X2-Intenmediale node
X3- o/p node
Ab- forward path (p)
Bc- 1 loop (L)
At node XQ:
X2 = x1a + x3c [Add i/p signals at node]
At node x3:
x2b =x3
(x1a+x3c) b = x3
X1ab = x3 (1-bc)
X1 = x3 (1-bc)/ab
Ab/(1-bc) = x3/x1
T= p/1-L

X1:- I/p node x2, x3,x4,x5,Qnlexmedili node
X0:- o/p node abdeg:- forward path
Bc, ef :- Loop [isolated]
x2 = ax1+c x3
x3= bx2
x4 = d x3+f x5
x5 = e x4
x6= g x5
x6 = g(e x4) = ge [dx3+ e f x5]
xb = ge [d (bx2) + f (e x4)]
xb = ge [ db (ax1+cx3) + fe (dx3+ fx5)]
xb = ge [db (ax1+cb (ax1+x3) +fe[cdbx2]+
f( e [db (ax1+ cx3)
x2 = ax1 + cb (x2) x4 = d bx2 + f exq
x2 = ax1 + cbx2 = db (d4) + fe/1-cb
x2 = ax1/(1-cb) xy = db x2 + f x6/g
xy = db [ax1]/1-cb + f xb/g
x5 = c db ( ax1)/1-cb + efxb/g
xb = gx5
= gedb (ax1)/1-cb + g efxb/g
Xb = gx5
Gedb (ax1)/1-cb + g efxb/g
(1-gef/g) xb = gedb ax1/1-ab
Xb/x1 = gedb a/ (1- ef – bc + beef
Xb/x1 = p/ 1- (L1+L2) + L1 L2for isolated loops
Q3) Reduce given B.D to canonical (simple form) and hence obtain the equivalent Tf = c(s)/ R(S)?
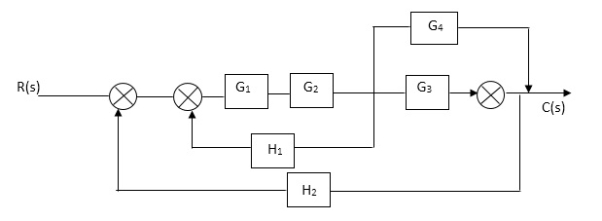
A3)

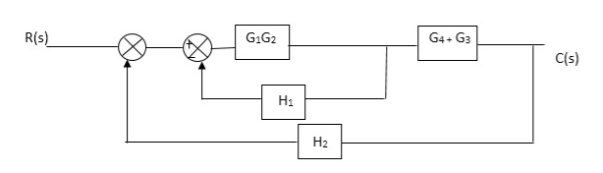
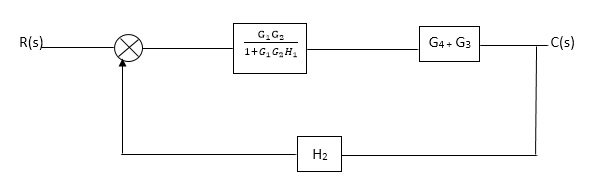
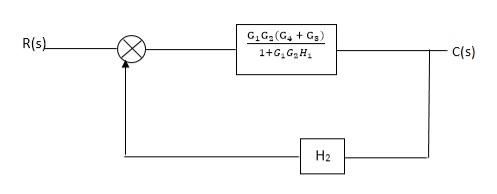
Fig. Final reduced block diagram
C(S)/R(S) = (G1G2) (G3+G4)/1+G1G2H1)/1-G1,G2(G3+G4) H2/1+G1G2H1
= G1G2(G3+G4)/1+G1G2H1-G1G2H2(G3+G4)
=G1G2(G3+G4)/1+(H1-H2)(G1G2) (G3+G4)
C(s)/R(S) = G1G2(G3+G4)/1+(H1-H2(G3+G4)) G1 G2
Q4) Reduce using Masons gain formula
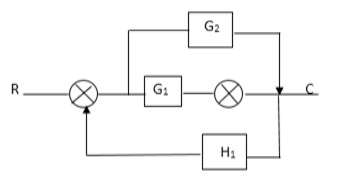
A4)

P1= G1 p2 =G2 Delta1 =1
L1= -G1 H1
 = 1-(-G1H1)
= 1-(-G1H1)
= 1+G1H1
T= G1+G2/1+G1H1
Q5) Determine overall gain reliably x5 and x1 Draw SFG
X2 = ax1+ f x2
X3= bx2 +exy
X4 = cx3+hx5
X5 =dx4 + gx2
A5)
P1 = abcd p2 = ag
L1 = f L2 = ce, L3= dh
 1 = 1
1 = 1
 2= 1-ce
2= 1-ce
 = 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[f+ le = dh] + [fce +fdh]
T= abcd+ ag (1-ce)/1-[ftce + dh ] + (fce + fdh)
Q6) Draw the free body diagram and write the differential equation for system below.
A6)
The free body diagram for M1 will be
F(t) = M1 d2/dt2x1+ B1 d/dt (x1-x2)+ k1(x1-x2)
Similarly for M2we have
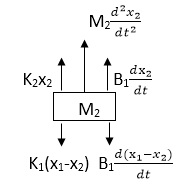
K1(x1-x2) + B1d/dt(x1-x2) = k2x2+M2d2/dt2+B2dx2/dt
Q7) For the given mechanical system below draw the analogus system (force. Voltage) & find V0(s)/V1(s)
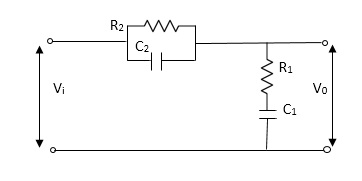
A7)
Let Z1 = R2 11 1/c2
=R2*1/c2s/R2+1/c2s
Z1= R2/1+R2c2s
Let Z2 = R1+1/c1s
Z2= 1+R1c1s/c1s
V0(s)/vi(s) = z2/z1+z2
=1+R1c1s/c1s/R2/1+R2c2s+1+R1c1s/c1s
V0(s)/v0(s) =(c1+R1c1s) (1+R2c2s)/R2c1s+1+sR1c1s2R1R2c1c2
Q8) Explain force-voltage analogy?
A8)
If the dynamic characteristics of an electrical system is identical to that of a mechanical system, then the electrical system is said to be analogous to the mechanical system. This can be done by comparing the mathematical models of both the systems.
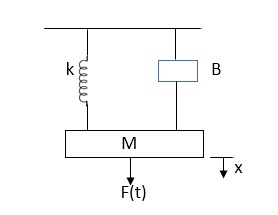
Fig. Mechanical System
The equation for above mechanical system is given by
f(t) = M 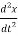 +B
+B  +kx (1)
+kx (1)
For series RLC circuit the mathematical equation is given as
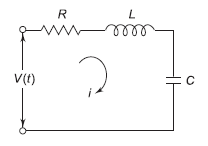
Fig. Electrical System
V(t)= Ri + L 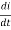 +
+ 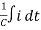
i = 
V(t) = L 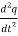 + R
+ R +
+  (2)
(2)
Comparing 1 and 2 we see that
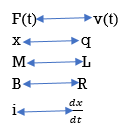
Q9) Explain force-current analogy?
A9)
For parallel RLC circuit shown below the KCL equation is written as
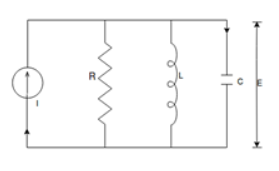
Fig. Electrical Circuit
i(t) = C 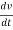 +
+  +
+ 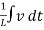
v = 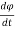
i(t) = C  + R
+ R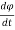 +
+ 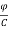 (3)
(3)
Comparing 1 and 3 we find that
Q10) Reduce the give block diagram to find the transfer function?
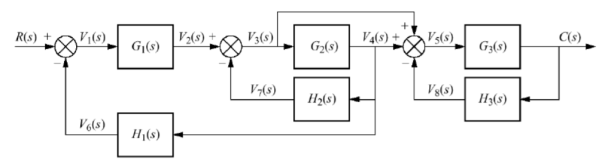
A10)
The above block diagram can be reduced as shown below
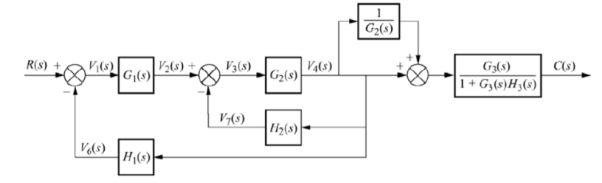
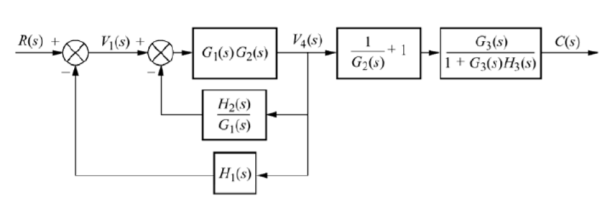
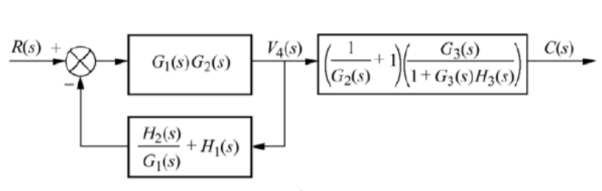

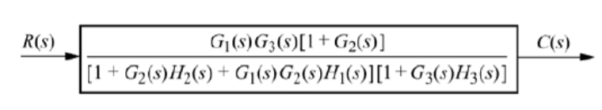
From above reduced figure the transfer function is very clear.
Q11) Reduce the given figure using block diagram reduction to find its transfer function?
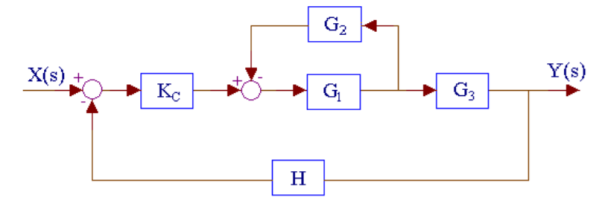
A11)
The above system can be reduced as

Kc, (G1/1+G1G2) and G3 are in series. H is in feedback with them.

Q12) Reduce the given system using block diagram reduction technique?
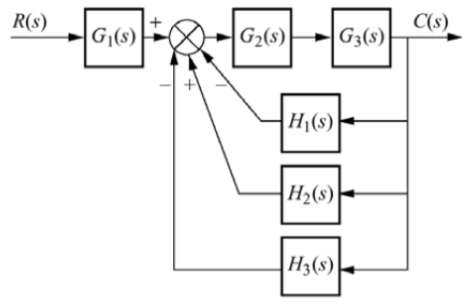
A12)
The figure can be reduced as
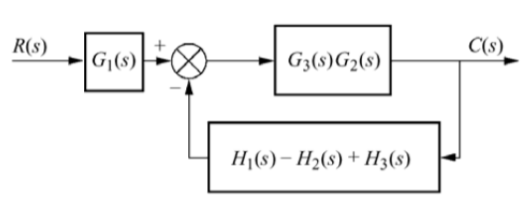
G1 and G2 are in series and H1, H2 and H3 are in parallel.
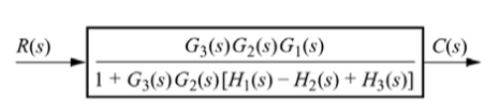
G1 is in series with feedback configuration. The transfer function becomes
C(s)/R(s) =
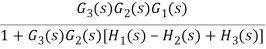
Q13) Compute the transfer function of the given figure?
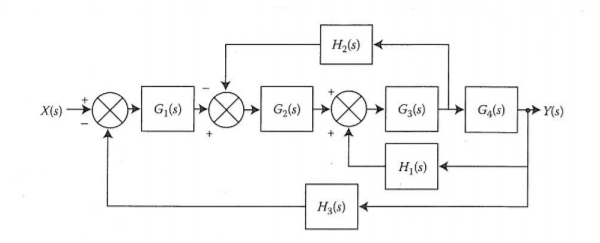
A13)
The branch point at the left of the block with transfer function G4(s) is moved at the right of G4(s). The equivalent block diagram is

The transformation is applied to blocks with transfer function G3(s), G4(s) and H1(s).
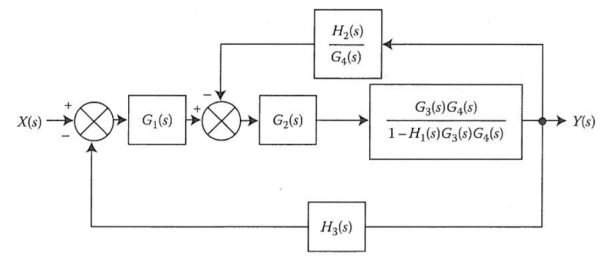
We apply transformation to the loop with TF H2(s)/G4(s) we get
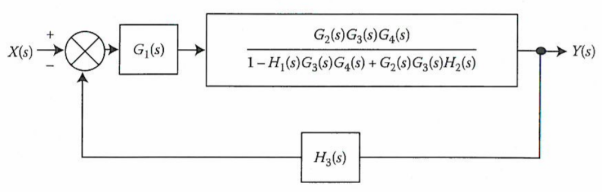
Again, applying same transformation to above figure we get the final reduced structure

Q14) Derive the transfer function of thermal system?
A14)
Thermal systems are those that involve the transfer of heat from one substance to another. The model of thermal systems is obtained by using thermal resistance and capacitance which are the basic elements of the thermal system. The thermal resistance and capacitance are distributed in nature. But for simplicity in analysis lumped parameter models are used.
Consider a simple thermal system shown in the below figure. Let us assume that the tank is insulated to eliminate heat loss to the surrounding air, there is no heat storage in the insulation and liquid in the tank is kept at uniform temperature by perfect mixing with the help of a stirrer. Thus, a single temperature is used to describe the temperature of the liquid in the tank and of the out flowing liquid. The transfer function of thermal system can be derived as shown below.
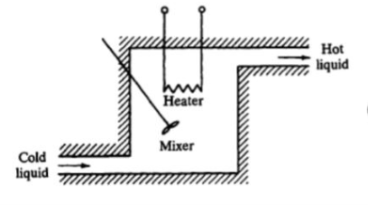
Fig. Thermal System
Let θ1 = Steady state temperature of inflowing liquid, °C
θ0 = Sandy state temperature of outflowing liquid, °C
G = Steady state liquid flow rate, Kg/sec
M = Mass of liquid in tank, Kg
c = Specific heat of liquid, Kcal/Kg °C
R = Thermal resistance, °C - sec/Kcal
C = Thermal capacitance, Kcal/°C
Q = Steady state heat input rate, Kcal/Sec
Let us assume that the temperature of inflowing liquid is kept constant. Let the heat input rate to the thermal system supplied by the heater is suddenly changed from Q to Q + q1. Due to this, the heat output flow rate will gradually change from Q to Q + q0. The temperature of the outflowing liquid will also be changed from θ0 to θ0 + θ.
For this system the equation for q0, C and R is obtained as follows,
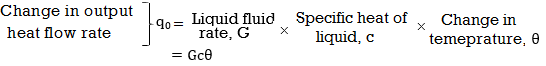
Thermal capacitance, C = Mass, M x Specific heat of liquid, c = Mc
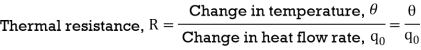
On substituting for qo from equation (1) in equation (3) we get,
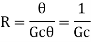
In this thermal system, rate of change of temperature is directly proportional to change in heat input rate.
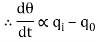
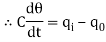
The constant of proportionality is capacitance C of the system.
Equation (5) is the differential equation governing system. Since, equation (5) is of first order equation, the system is first order system.
From equation (3), R = θ/q0
q0 = θ/R
On substituting for q0 from equation (6) in equation (5) we get,
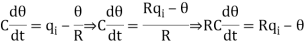
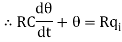
Let, L {θ} = θ(s); L{dθ/dt} = sθ(s) ; L{q1} = Q1(s)
On taking Laplace transform of equation (7)
RC s θ(s) + θ(s) = R Q1(s)
θ(s) [sRC + 1] = R Q1(s)
θ(s)/Q1(s) is the required transfer function of thermal system.
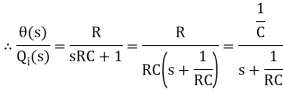
Unit - 1
Unit - 1
Introduction to need for automation and automatic control
Q1) Find SFG for the block diagram below?
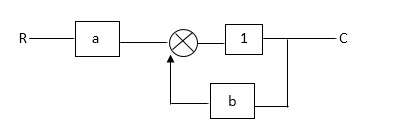
A1)
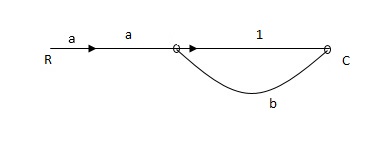
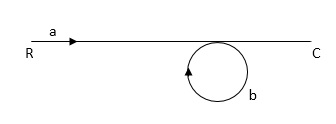
Ra+cb =c
c/R= a/1-b
Q2) The SFG shown has forward path and singles isolated loop determine overall transmittance relating X3 and X1?
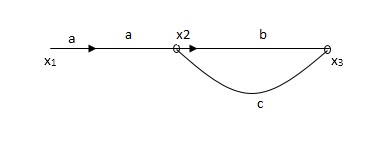
A2)
X1- I/p node
X2-Intenmediale node
X3- o/p node
Ab- forward path (p)
Bc- 1 loop (L)
At node XQ:
X2 = x1a + x3c [Add i/p signals at node]
At node x3:
x2b =x3
(x1a+x3c) b = x3
X1ab = x3 (1-bc)
X1 = x3 (1-bc)/ab
Ab/(1-bc) = x3/x1
T= p/1-L

X1:- I/p node x2, x3,x4,x5,Qnlexmedili node
X0:- o/p node abdeg:- forward path
Bc, ef :- Loop [isolated]
x2 = ax1+c x3
x3= bx2
x4 = d x3+f x5
x5 = e x4
x6= g x5
x6 = g(e x4) = ge [dx3+ e f x5]
xb = ge [d (bx2) + f (e x4)]
xb = ge [ db (ax1+cx3) + fe (dx3+ fx5)]
xb = ge [db (ax1+cb (ax1+x3) +fe[cdbx2]+
f( e [db (ax1+ cx3)
x2 = ax1 + cb (x2) x4 = d bx2 + f exq
x2 = ax1 + cbx2 = db (d4) + fe/1-cb
x2 = ax1/(1-cb) xy = db x2 + f x6/g
xy = db [ax1]/1-cb + f xb/g
x5 = c db ( ax1)/1-cb + efxb/g
xb = gx5
= gedb (ax1)/1-cb + g efxb/g
Xb = gx5
Gedb (ax1)/1-cb + g efxb/g
(1-gef/g) xb = gedb ax1/1-ab
Xb/x1 = gedb a/ (1- ef – bc + beef
Xb/x1 = p/ 1- (L1+L2) + L1 L2for isolated loops
Q3) Reduce given B.D to canonical (simple form) and hence obtain the equivalent Tf = c(s)/ R(S)?

A3)
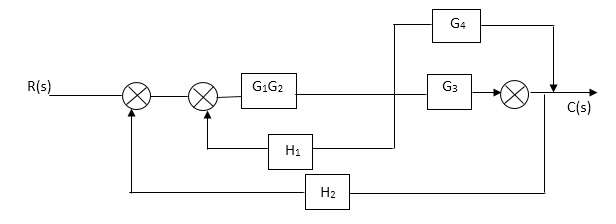
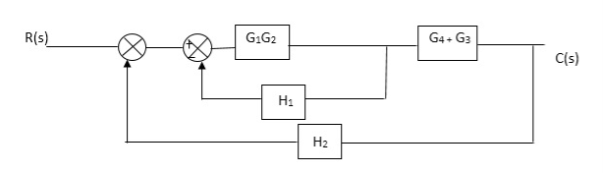
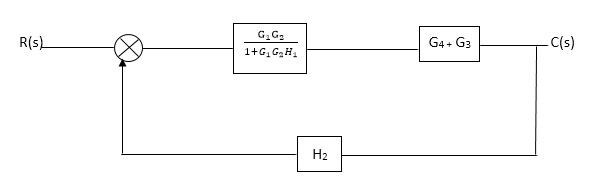
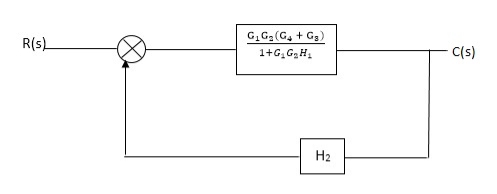
Fig. Final reduced block diagram
C(S)/R(S) = (G1G2) (G3+G4)/1+G1G2H1)/1-G1,G2(G3+G4) H2/1+G1G2H1
= G1G2(G3+G4)/1+G1G2H1-G1G2H2(G3+G4)
=G1G2(G3+G4)/1+(H1-H2)(G1G2) (G3+G4)
C(s)/R(S) = G1G2(G3+G4)/1+(H1-H2(G3+G4)) G1 G2
Q4) Reduce using Masons gain formula
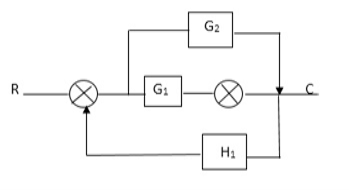
A4)
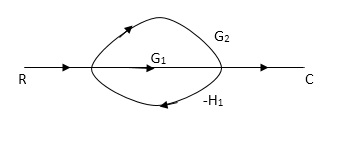
P1= G1 p2 =G2 Delta1 =1
L1= -G1 H1
 = 1-(-G1H1)
= 1-(-G1H1)
= 1+G1H1
T= G1+G2/1+G1H1
Q5) Determine overall gain reliably x5 and x1 Draw SFG
X2 = ax1+ f x2
X3= bx2 +exy
X4 = cx3+hx5
X5 =dx4 + gx2
A5)
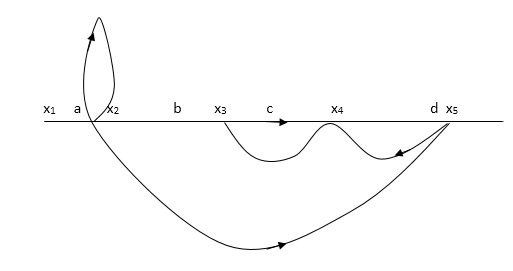
P1 = abcd p2 = ag
L1 = f L2 = ce, L3= dh
 1 = 1
1 = 1
 2= 1-ce
2= 1-ce
 = 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[f+ le = dh] + [fce +fdh]
T= abcd+ ag (1-ce)/1-[ftce + dh ] + (fce + fdh)
Q6) Draw the free body diagram and write the differential equation for system below.
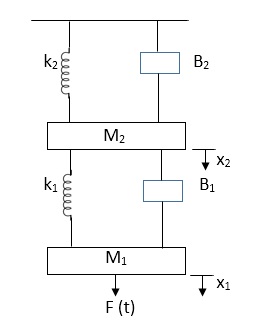
A6)
The free body diagram for M1 will be
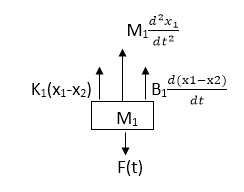
F(t) = M1 d2/dt2x1+ B1 d/dt (x1-x2)+ k1(x1-x2)
Similarly for M2we have
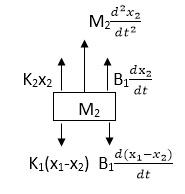
K1(x1-x2) + B1d/dt(x1-x2) = k2x2+M2d2/dt2+B2dx2/dt
Q7) For the given mechanical system below draw the analogus system (force. Voltage) & find V0(s)/V1(s)
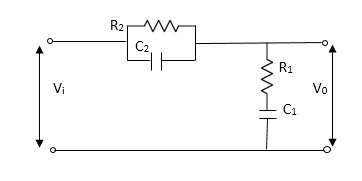
A7)
Let Z1 = R2 11 1/c2
=R2*1/c2s/R2+1/c2s
Z1= R2/1+R2c2s
Let Z2 = R1+1/c1s
Z2= 1+R1c1s/c1s
V0(s)/vi(s) = z2/z1+z2
=1+R1c1s/c1s/R2/1+R2c2s+1+R1c1s/c1s
V0(s)/v0(s) =(c1+R1c1s) (1+R2c2s)/R2c1s+1+sR1c1s2R1R2c1c2
Q8) Explain force-voltage analogy?
A8)
If the dynamic characteristics of an electrical system is identical to that of a mechanical system, then the electrical system is said to be analogous to the mechanical system. This can be done by comparing the mathematical models of both the systems.
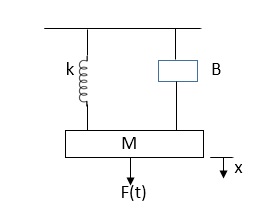
Fig. Mechanical System
The equation for above mechanical system is given by
f(t) = M 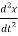 +B
+B 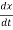 +kx (1)
+kx (1)
For series RLC circuit the mathematical equation is given as
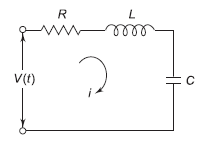
Fig. Electrical System
V(t)= Ri + L  +
+ 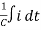
i = 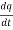
V(t) = L 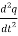 + R
+ R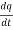 +
+  (2)
(2)
Comparing 1 and 2 we see that
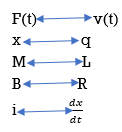
Q9) Explain force-current analogy?
A9)
For parallel RLC circuit shown below the KCL equation is written as
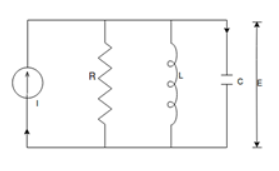
Fig. Electrical Circuit
i(t) = C 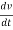 +
+  +
+ 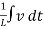
v = 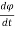
i(t) = C 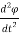 + R
+ R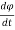 +
+ 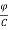 (3)
(3)
Comparing 1 and 3 we find that
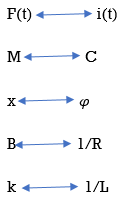
Q10) Reduce the give block diagram to find the transfer function?
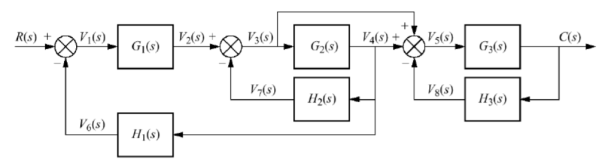
A10)
The above block diagram can be reduced as shown below
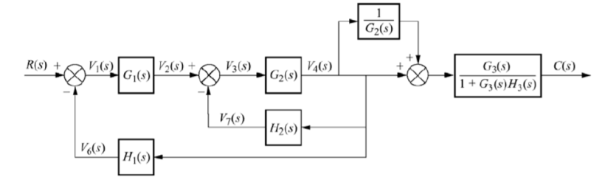
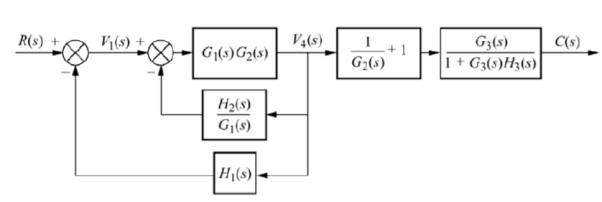
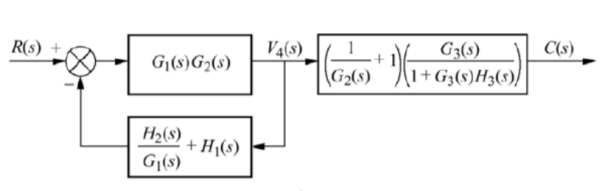


From above reduced figure the transfer function is very clear.
Q11) Reduce the given figure using block diagram reduction to find its transfer function?
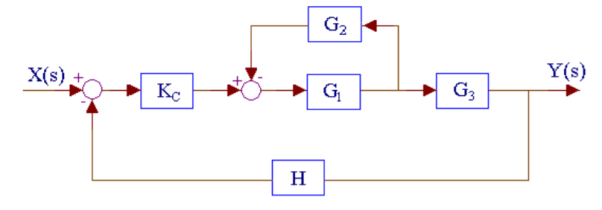
A11)
The above system can be reduced as
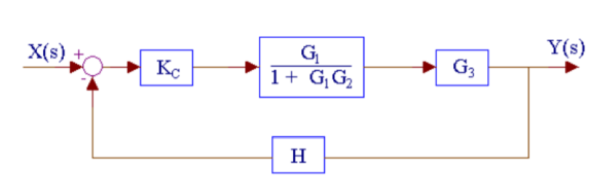
Kc, (G1/1+G1G2) and G3 are in series. H is in feedback with them.
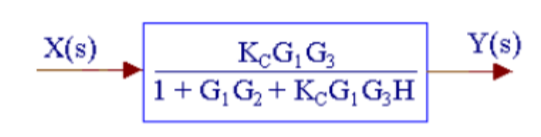
Q12) Reduce the given system using block diagram reduction technique?
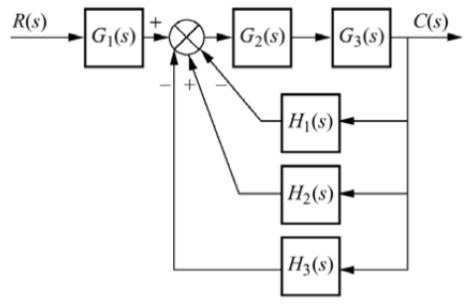
A12)
The figure can be reduced as

G1 and G2 are in series and H1, H2 and H3 are in parallel.
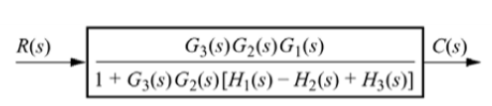
G1 is in series with feedback configuration. The transfer function becomes
C(s)/R(s) =
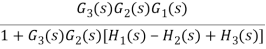
Q13) Compute the transfer function of the given figure?
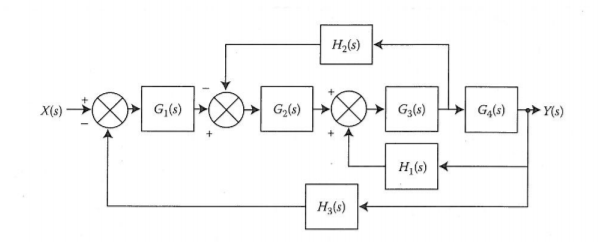
A13)
The branch point at the left of the block with transfer function G4(s) is moved at the right of G4(s). The equivalent block diagram is
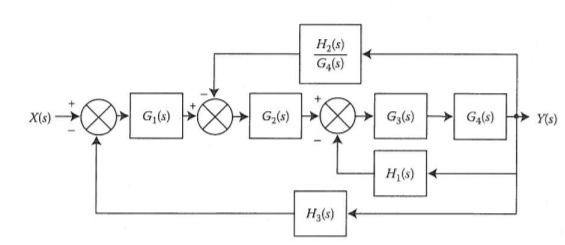
The transformation is applied to blocks with transfer function G3(s), G4(s) and H1(s).
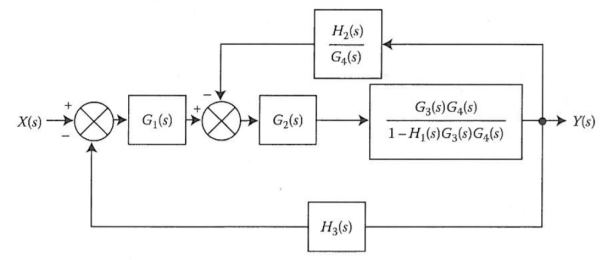
We apply transformation to the loop with TF H2(s)/G4(s) we get
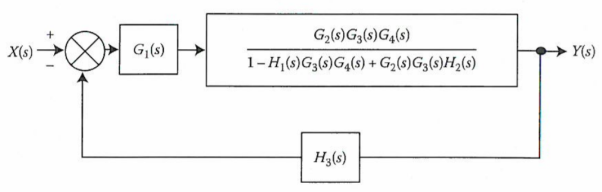
Again, applying same transformation to above figure we get the final reduced structure

Q14) Derive the transfer function of thermal system?
A14)
Thermal systems are those that involve the transfer of heat from one substance to another. The model of thermal systems is obtained by using thermal resistance and capacitance which are the basic elements of the thermal system. The thermal resistance and capacitance are distributed in nature. But for simplicity in analysis lumped parameter models are used.
Consider a simple thermal system shown in the below figure. Let us assume that the tank is insulated to eliminate heat loss to the surrounding air, there is no heat storage in the insulation and liquid in the tank is kept at uniform temperature by perfect mixing with the help of a stirrer. Thus, a single temperature is used to describe the temperature of the liquid in the tank and of the out flowing liquid. The transfer function of thermal system can be derived as shown below.
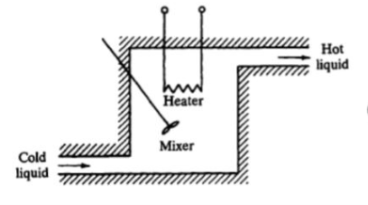
Fig. Thermal System
Let θ1 = Steady state temperature of inflowing liquid, °C
θ0 = Sandy state temperature of outflowing liquid, °C
G = Steady state liquid flow rate, Kg/sec
M = Mass of liquid in tank, Kg
c = Specific heat of liquid, Kcal/Kg °C
R = Thermal resistance, °C - sec/Kcal
C = Thermal capacitance, Kcal/°C
Q = Steady state heat input rate, Kcal/Sec
Let us assume that the temperature of inflowing liquid is kept constant. Let the heat input rate to the thermal system supplied by the heater is suddenly changed from Q to Q + q1. Due to this, the heat output flow rate will gradually change from Q to Q + q0. The temperature of the outflowing liquid will also be changed from θ0 to θ0 + θ.
For this system the equation for q0, C and R is obtained as follows,
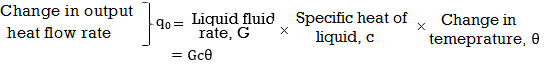
Thermal capacitance, C = Mass, M x Specific heat of liquid, c = Mc

On substituting for qo from equation (1) in equation (3) we get,
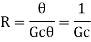
In this thermal system, rate of change of temperature is directly proportional to change in heat input rate.
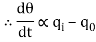
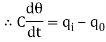
The constant of proportionality is capacitance C of the system.
Equation (5) is the differential equation governing system. Since, equation (5) is of first order equation, the system is first order system.
From equation (3), R = θ/q0
q0 = θ/R
On substituting for q0 from equation (6) in equation (5) we get,
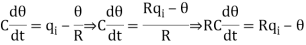
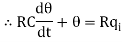
Let, L {θ} = θ(s); L{dθ/dt} = sθ(s) ; L{q1} = Q1(s)
On taking Laplace transform of equation (7)
RC s θ(s) + θ(s) = R Q1(s)
θ(s) [sRC + 1] = R Q1(s)
θ(s)/Q1(s) is the required transfer function of thermal system.
Unit - 1
Unit - 1
Introduction to need for automation and automatic control
Q1) Find SFG for the block diagram below?

A1)
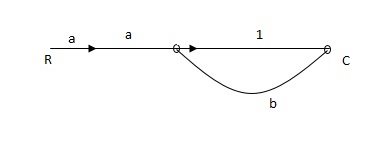
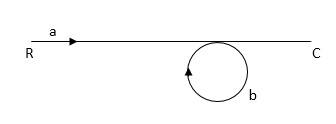
Ra+cb =c
c/R= a/1-b
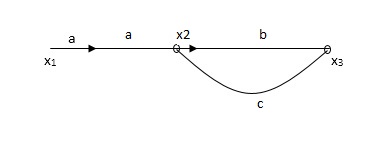
Q2) The SFG shown has forward path and singles isolated loop determine overall transmittance relating X3 and X1?
A2)
X1- I/p node
X2-Intenmediale node
X3- o/p node
Ab- forward path (p)
Bc- 1 loop (L)
At node XQ:
X2 = x1a + x3c [Add i/p signals at node]
At node x3:
x2b =x3
(x1a+x3c) b = x3
X1ab = x3 (1-bc)
X1 = x3 (1-bc)/ab
Ab/(1-bc) = x3/x1
T= p/1-L

X1:- I/p node x2, x3,x4,x5,Qnlexmedili node
X0:- o/p node abdeg:- forward path
Bc, ef :- Loop [isolated]
x2 = ax1+c x3
x3= bx2
x4 = d x3+f x5
x5 = e x4
x6= g x5
x6 = g(e x4) = ge [dx3+ e f x5]
xb = ge [d (bx2) + f (e x4)]
xb = ge [ db (ax1+cx3) + fe (dx3+ fx5)]
xb = ge [db (ax1+cb (ax1+x3) +fe[cdbx2]+
f( e [db (ax1+ cx3)
x2 = ax1 + cb (x2) x4 = d bx2 + f exq
x2 = ax1 + cbx2 = db (d4) + fe/1-cb
x2 = ax1/(1-cb) xy = db x2 + f x6/g
xy = db [ax1]/1-cb + f xb/g
x5 = c db ( ax1)/1-cb + efxb/g
xb = gx5
= gedb (ax1)/1-cb + g efxb/g
Xb = gx5
Gedb (ax1)/1-cb + g efxb/g
(1-gef/g) xb = gedb ax1/1-ab
Xb/x1 = gedb a/ (1- ef – bc + beef
Xb/x1 = p/ 1- (L1+L2) + L1 L2for isolated loops
Q3) Reduce given B.D to canonical (simple form) and hence obtain the equivalent Tf = c(s)/ R(S)?
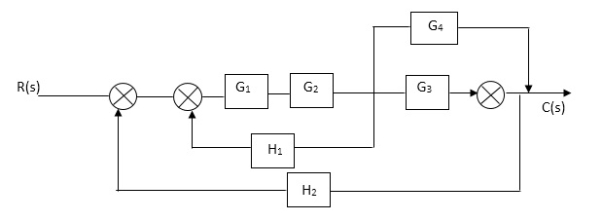
A3)
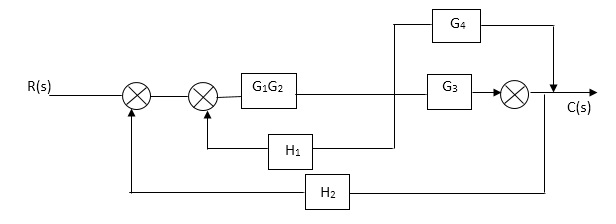
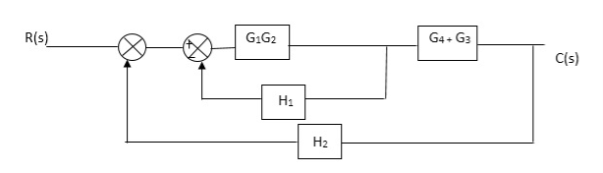
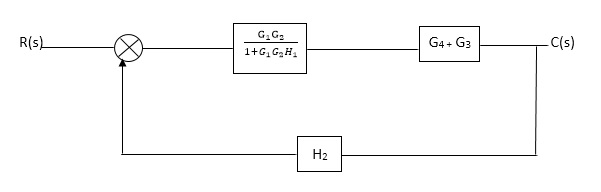
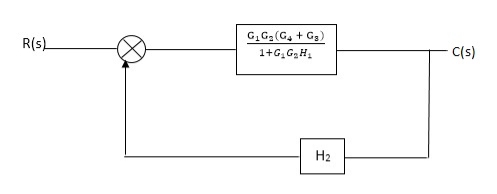
Fig. Final reduced block diagram
C(S)/R(S) = (G1G2) (G3+G4)/1+G1G2H1)/1-G1,G2(G3+G4) H2/1+G1G2H1
= G1G2(G3+G4)/1+G1G2H1-G1G2H2(G3+G4)
=G1G2(G3+G4)/1+(H1-H2)(G1G2) (G3+G4)
C(s)/R(S) = G1G2(G3+G4)/1+(H1-H2(G3+G4)) G1 G2
Q4) Reduce using Masons gain formula
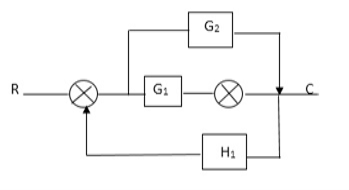
A4)
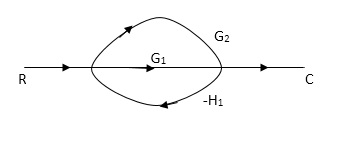
P1= G1 p2 =G2 Delta1 =1
L1= -G1 H1
 = 1-(-G1H1)
= 1-(-G1H1)
= 1+G1H1
T= G1+G2/1+G1H1
Q5) Determine overall gain reliably x5 and x1 Draw SFG
X2 = ax1+ f x2
X3= bx2 +exy
X4 = cx3+hx5
X5 =dx4 + gx2
A5)
P1 = abcd p2 = ag
L1 = f L2 = ce, L3= dh
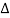 1 = 1
1 = 1
 2= 1-ce
2= 1-ce
 = 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[f+ le = dh] + [fce +fdh]
T= abcd+ ag (1-ce)/1-[ftce + dh ] + (fce + fdh)
Q6) Draw the free body diagram and write the differential equation for system below.

A6)
The free body diagram for M1 will be
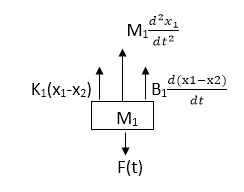
F(t) = M1 d2/dt2x1+ B1 d/dt (x1-x2)+ k1(x1-x2)
Similarly for M2we have
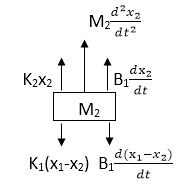
K1(x1-x2) + B1d/dt(x1-x2) = k2x2+M2d2/dt2+B2dx2/dt
Q7) For the given mechanical system below draw the analogus system (force. Voltage) & find V0(s)/V1(s)

A7)
Let Z1 = R2 11 1/c2
=R2*1/c2s/R2+1/c2s
Z1= R2/1+R2c2s
Let Z2 = R1+1/c1s
Z2= 1+R1c1s/c1s
V0(s)/vi(s) = z2/z1+z2
=1+R1c1s/c1s/R2/1+R2c2s+1+R1c1s/c1s
V0(s)/v0(s) =(c1+R1c1s) (1+R2c2s)/R2c1s+1+sR1c1s2R1R2c1c2
Q8) Explain force-voltage analogy?
A8)
If the dynamic characteristics of an electrical system is identical to that of a mechanical system, then the electrical system is said to be analogous to the mechanical system. This can be done by comparing the mathematical models of both the systems.
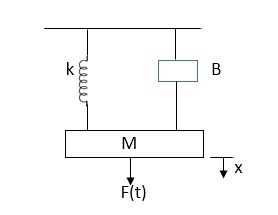
Fig. Mechanical System
The equation for above mechanical system is given by
f(t) = M 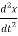 +B
+B 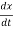 +kx (1)
+kx (1)
For series RLC circuit the mathematical equation is given as
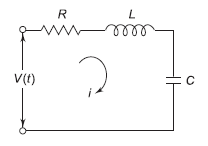
Fig. Electrical System
V(t)= Ri + L 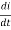 +
+ 
i = 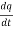
V(t) = L 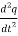 + R
+ R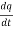 +
+  (2)
(2)
Comparing 1 and 2 we see that
Q9) Explain force-current analogy?
A9)
For parallel RLC circuit shown below the KCL equation is written as
Fig. Electrical Circuit
i(t) = C  +
+  +
+ 
v = 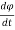
i(t) = C 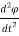 + R
+ R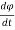 +
+ 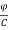 (3)
(3)
Comparing 1 and 3 we find that
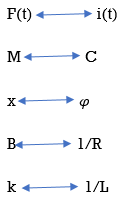
Q10) Reduce the give block diagram to find the transfer function?
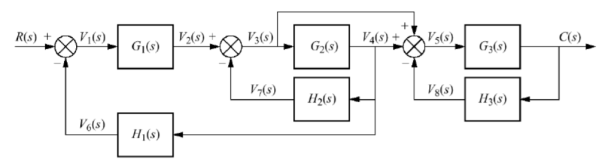
A10)
The above block diagram can be reduced as shown below
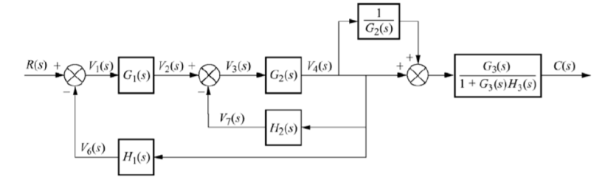

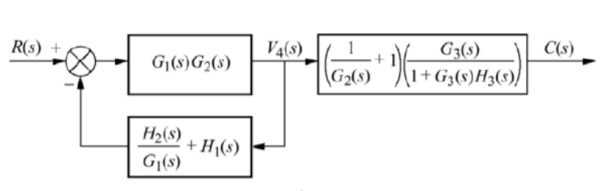

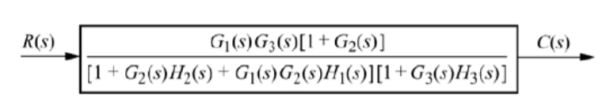
From above reduced figure the transfer function is very clear.
Q11) Reduce the given figure using block diagram reduction to find its transfer function?

A11)
The above system can be reduced as
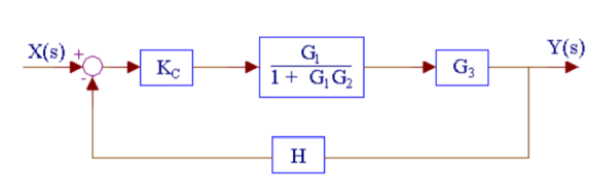
Kc, (G1/1+G1G2) and G3 are in series. H is in feedback with them.
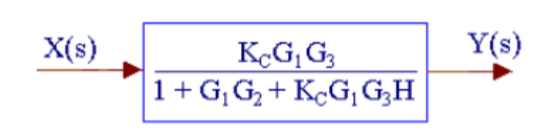
Q12) Reduce the given system using block diagram reduction technique?
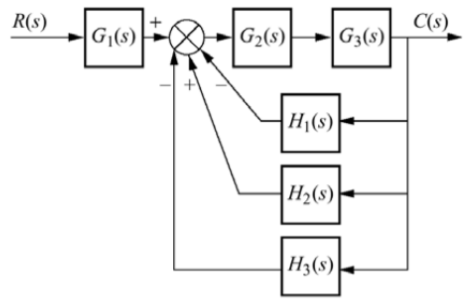
A12)
The figure can be reduced as
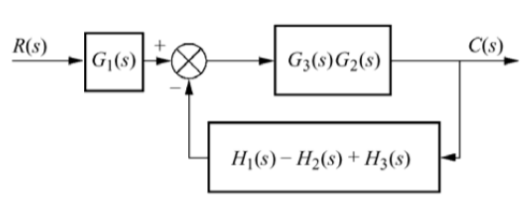
G1 and G2 are in series and H1, H2 and H3 are in parallel.
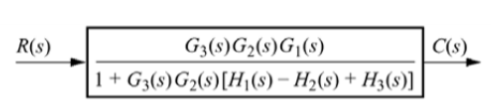
G1 is in series with feedback configuration. The transfer function becomes
C(s)/R(s) =
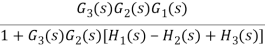
Q13) Compute the transfer function of the given figure?
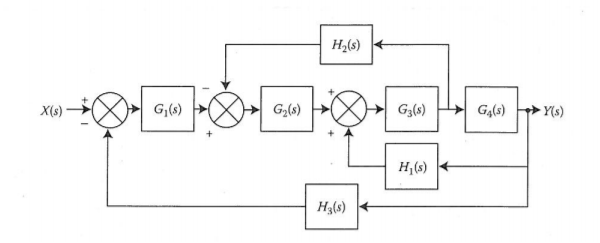
A13)
The branch point at the left of the block with transfer function G4(s) is moved at the right of G4(s). The equivalent block diagram is
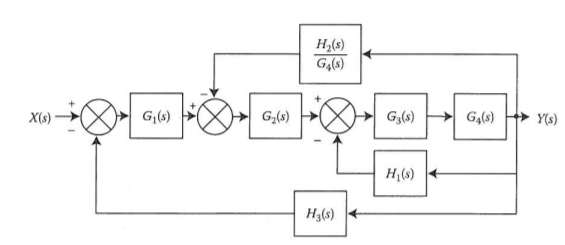
The transformation is applied to blocks with transfer function G3(s), G4(s) and H1(s).
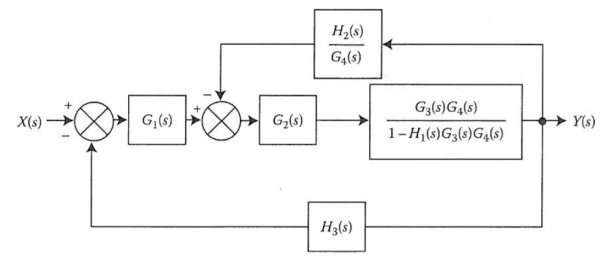
We apply transformation to the loop with TF H2(s)/G4(s) we get
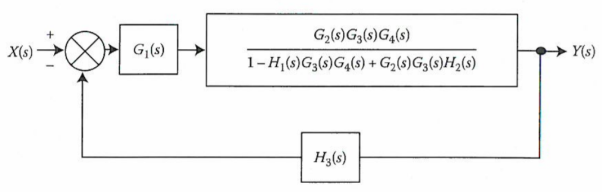
Again, applying same transformation to above figure we get the final reduced structure

Q14) Derive the transfer function of thermal system?
A14)
Thermal systems are those that involve the transfer of heat from one substance to another. The model of thermal systems is obtained by using thermal resistance and capacitance which are the basic elements of the thermal system. The thermal resistance and capacitance are distributed in nature. But for simplicity in analysis lumped parameter models are used.
Consider a simple thermal system shown in the below figure. Let us assume that the tank is insulated to eliminate heat loss to the surrounding air, there is no heat storage in the insulation and liquid in the tank is kept at uniform temperature by perfect mixing with the help of a stirrer. Thus, a single temperature is used to describe the temperature of the liquid in the tank and of the out flowing liquid. The transfer function of thermal system can be derived as shown below.
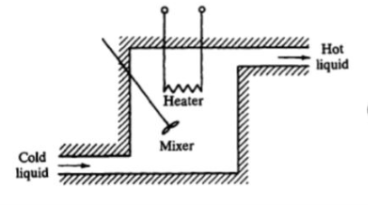
Fig. Thermal System
Let θ1 = Steady state temperature of inflowing liquid, °C
θ0 = Sandy state temperature of outflowing liquid, °C
G = Steady state liquid flow rate, Kg/sec
M = Mass of liquid in tank, Kg
c = Specific heat of liquid, Kcal/Kg °C
R = Thermal resistance, °C - sec/Kcal
C = Thermal capacitance, Kcal/°C
Q = Steady state heat input rate, Kcal/Sec
Let us assume that the temperature of inflowing liquid is kept constant. Let the heat input rate to the thermal system supplied by the heater is suddenly changed from Q to Q + q1. Due to this, the heat output flow rate will gradually change from Q to Q + q0. The temperature of the outflowing liquid will also be changed from θ0 to θ0 + θ.
For this system the equation for q0, C and R is obtained as follows,
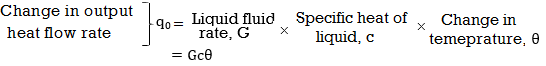
Thermal capacitance, C = Mass, M x Specific heat of liquid, c = Mc
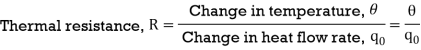
On substituting for qo from equation (1) in equation (3) we get,

In this thermal system, rate of change of temperature is directly proportional to change in heat input rate.
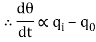
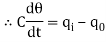
The constant of proportionality is capacitance C of the system.
Equation (5) is the differential equation governing system. Since, equation (5) is of first order equation, the system is first order system.
From equation (3), R = θ/q0
q0 = θ/R
On substituting for q0 from equation (6) in equation (5) we get,
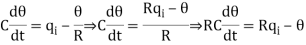
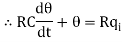
Let, L {θ} = θ(s); L{dθ/dt} = sθ(s) ; L{q1} = Q1(s)
On taking Laplace transform of equation (7)
RC s θ(s) + θ(s) = R Q1(s)
θ(s) [sRC + 1] = R Q1(s)
θ(s)/Q1(s) is the required transfer function of thermal system.