UNIT -1:
Q1: Find the nth derivative of
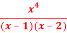
Solution:
Since 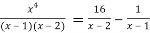
Differentiating both side with respect to x
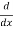 [
[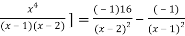
Again differentiating with respect to x

Again differentiating with respect to x
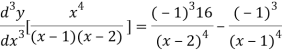
Similarly the nth derivative is
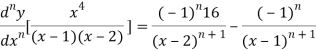
Q2: Find the nth derivative of 
Solution:
Let 
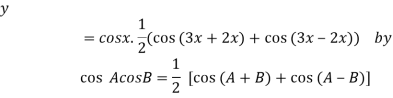
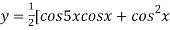 ]
]

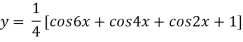
Differentiating with respect to x we get
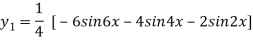
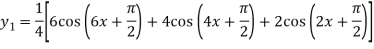
Again differentiating with respect to x we get
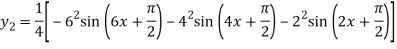
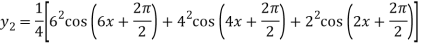
Again differentiating with respect to x we get
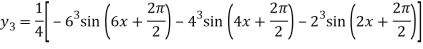
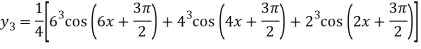
Similarly Again differentiating with respect to x we get
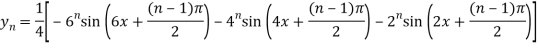
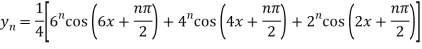
Q3: Find the nth derivative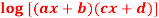
Solution:
Let 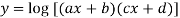
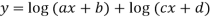
Differentiating with respect to x.
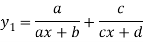
Again differentiating with respect to x.
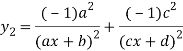
Again differentiating with respect to x.
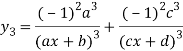
Again differentiating with respect to x.
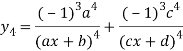
Again differentiating with respect to x.
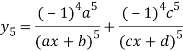
Similarly the nth derivative with respect to x.
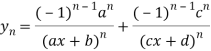
Q4: Expand the polynomial  in power of
in power of  , by Taylor’s theorem.
, by Taylor’s theorem.
Solution:
Let 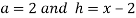 .
.
Also 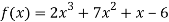
Then 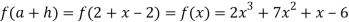
Differentiating with respect to x.
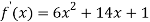
Again differentiating with respect to x the above function.
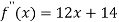
Again differentiating with respect to x the above function.
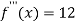
Also the value of above functions at x=2 will be
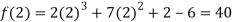
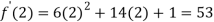
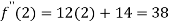
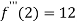
By Taylor’s theorem
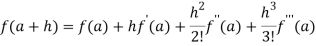
On substituting above values we get
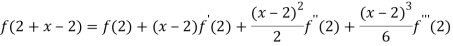
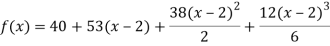
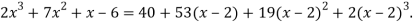
Q5: Expand  in power of
in power of 
Solution:
Let 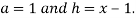
Also 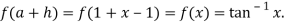
Differentiating f(x) with respect to x.
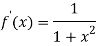
Again differentiating f(x) with respect to x.
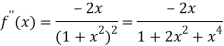
Again differentiating f(x) with respect to x.

Also the value of above functions at x=1 will be

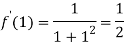
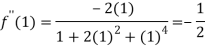

By Taylor’s theorem
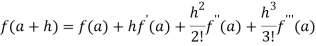
On substituting above values we get
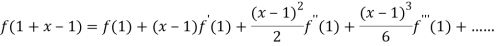
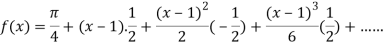
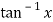 =
= 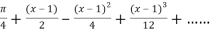
Q6: Expand  in power of
in power of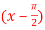 . Hence find the value of
. Hence find the value of  correct to four decimal places.
correct to four decimal places.
Solution:
Let 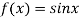
And 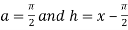 .
.
Differentiating 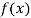 with respect to x.
with respect to x.

Again differentiating  with respect to x.
with respect to x.
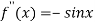
Again differentiating 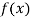 with respect to x.
with respect to x.
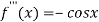
Again differentiating  with respect to x.
with respect to x.

Also the value of above functions at 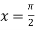 will be
will be
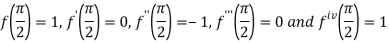
By Taylor’s theorem
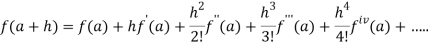
On substituting above values we get
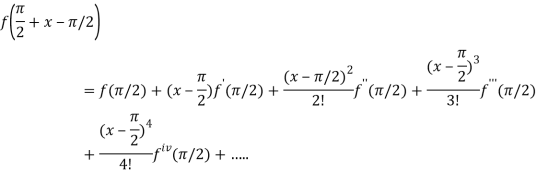
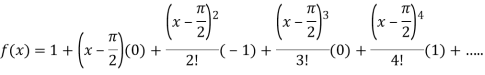
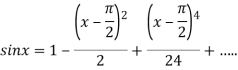
At 
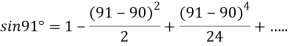
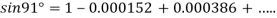
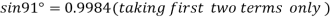 .
.
Q7: If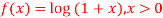 using Taylor’s theorem, show that for
using Taylor’s theorem, show that for  .
.
Solution:
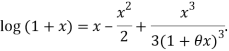
Deduce that 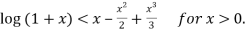
Let 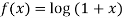 then
then 
Differentiating with respect to x.
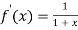 .Then
.Then
Again differentiating with respect to x.
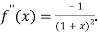 Then
Then 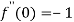
Again differentiating with respect to x.
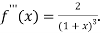 Then
Then 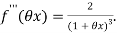
By Maclaurin’s theorem
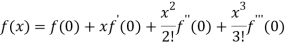
Substituting the above values we get
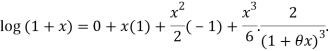
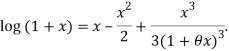
Since 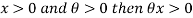
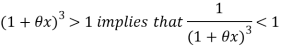
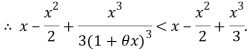
Hence 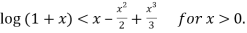
Q8: Prove that
Solution:
Let 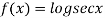
Differentiating 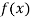 with respect to x.
with respect to x.
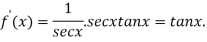
Again differentiating 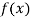 with respect to x.
with respect to x.

Again differentiating with respect to x.
with respect to x.
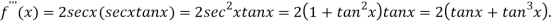
Again differentiating 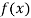 with respect to x.
with respect to x.
 and so on.
and so on.
Putting 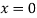 , in above derivatives we get
, in above derivatives we get
 so on.
so on.
By Maclaurin’s theorem
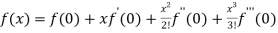 +………
+………
Substituting the above values we get
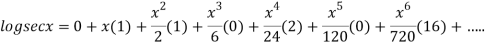

Q9:Prove that

Solution:
Let 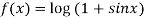
Differentiating above function with respect to x.
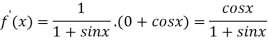
Again differentiating above function with respect to x.
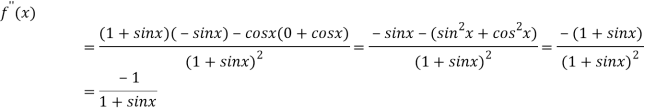
Again differentiating above function with respect to x.
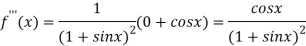
Again differentiating above function with respect to x.
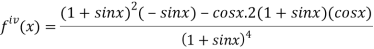

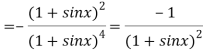
Putting 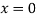 , in above derivatives we get
, in above derivatives we get
 so on.
so on.
By Maclaurin’s theorem
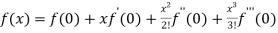 +………
+………
Substituting the above values we get
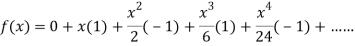
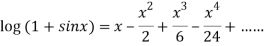
Q10:
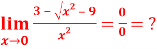
Solution:
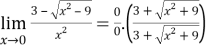
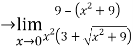

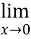
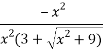
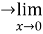
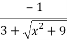 =
= 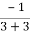 = 0
= 0
Q11:
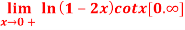 =?
=?
Solution:
=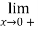
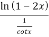
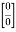
=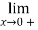
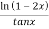
=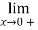

=-2
Q 12:
Find the radius of curvature for the following
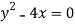
Solution:
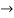 2y’’-4=0
2y’’-4=0
Y’=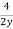 =
=
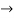 y’’=
y’’=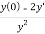 = -
= -
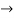 y’’.y2 = -2
y’’.y2 = -2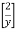
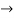 y’’=-
y’’=-
Substitute y=4, consider y’ and y’’ to solve for R:
We know that,
Radius of convergence (R) =  …..(1)
…..(1)
Now substituting the values y’ and y’’ in (1)
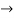
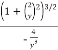 =
= 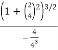 = 22.36
= 22.36
 Radius of convergence (R) =22.36
Radius of convergence (R) =22.36