UNIT 2

UNIT 2

Q 1: If

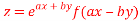
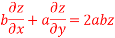
Solution:

Given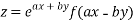 

   Partially differentiating z with respect to x keeping y as constant

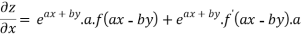
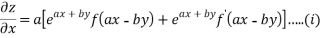
Again partially differentiating given z with respect to y keeping x as constant

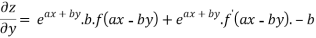
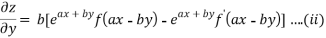
On b.eq(i) +a.eq(ii) we get

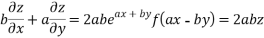
        Hence proved

Q 2: If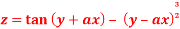

           Show that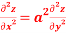

Solution:

Given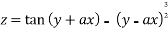 

Partially differentiating z with respect to x keeping y as constant

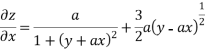
   Again partially differentiating z with respect to x keeping y as constant

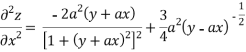
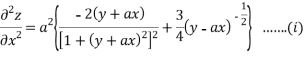
Partially differentiating z with respect to y keeping x as constant

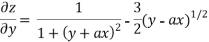
Again partially differentiating z with respect to y keeping x as constant

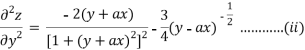
From eq(i) and eq(ii) we conclude that

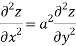
Q 3 : Find the value of n so that the equation

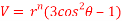
Satisfies the relation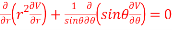 

Solution:

Given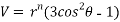   

  Partially differentiating V with respect to r keeping as constant

Again partially differentiating given V with respect to 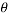keeping r as constant

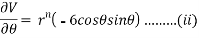
Now, we are taking the given relation

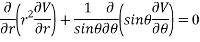
Substituting values using eq(i) and eq(ii)

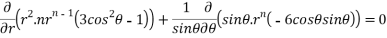
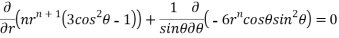
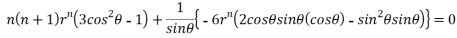
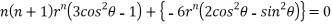
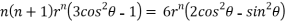
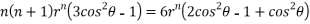
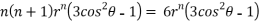
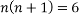
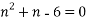
On solving we get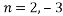 

Q 4: If 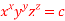then show that when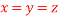

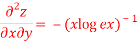
Solution:

      Given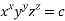 

     Taking log on both side we get

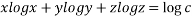
     Partially differentiating with respect to x we get

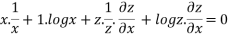
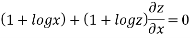
  …..(i)

         Similarly partially differentiating with respect y we get

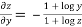    ……(ii)

           LHS 

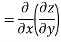
Substituting value from (ii)

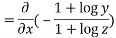
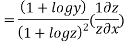
   Again substituting value from (i) we get

.()                

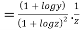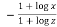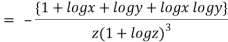
         When

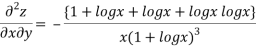
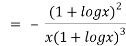
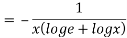
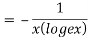
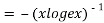
                =RHS

Hence proved

Q 5:If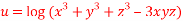

Then show that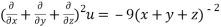 

Solution:

      Given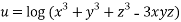 

Partially differentiating u with respect to x keeping y and z as constant

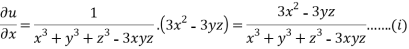
Similarly paritially differentiating u with respect to y keeping x and z as constant

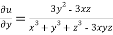  …….(ii)

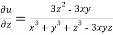  ……..(iii)

LHS: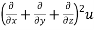 

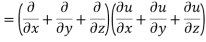
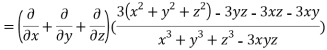
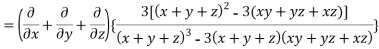
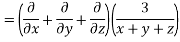
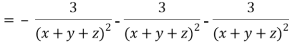
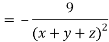
Hence proved

Q 6:

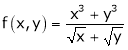
Solution:

Consider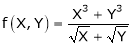

Put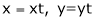

.

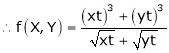
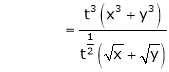
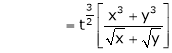
Thus degree of f(x, y) is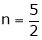

Note that

If 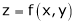be a homogeneous function of degree n then z can be written as

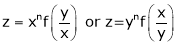
Q 7: Differentiate y = cos x2

Solution:

Given,

y = cos x2

Let u = x2, so that y = cos u

Therefore:  =2x

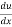= -sin u

And so, the chain rule says:

=  .

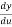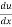
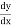= -sin u × 2x

= -2x sin x2

Q 7:

Differentiate f(x)=(1+x2)5.

Solution: 

Using the Chain rule,

=

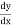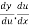
Let us take y = u5 and u = 1+x2

Then =  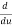(u5) = 5u4

=   (1 + x2 )= 2x. 

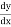= 5u4⋅2x = 5(1+x2)4⋅2x

= 10x(1+x4)

Q 8:

Find out the maxima and minima of the function

Solution:

   Given 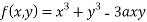    …(i)

         Partially differentiating (i) with respect to x we get

    ….(ii)

         Partially differentiating (i) with respect to y we get

    ….(iii)

          Now, form the equations

                    Using (ii) and (iii) we get

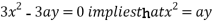
          using above two equations

                     Squaring both side we get

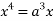
                      Or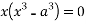 

                       This show that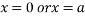

                         Also we get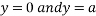

                 Thus we get the pair of value as

                  Now, we calculate

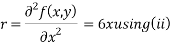
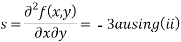
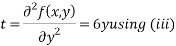
      Putting above values in

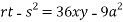
      At point (0,0)  we get

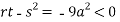
      So, the point (0,0) is a saddle point.

      At point 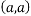we get

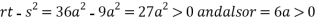
        So the point is the minimum point where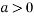

          In case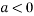 

         So the point 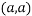is the maximum point where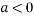

Q9:

 Find the maximum and minimum point of the function

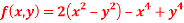
Solution:

        Partially differentiating given equation with respect to and x and y then equate them to zero                 

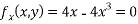
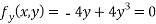
       On solving above we get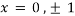 

         Also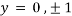

            Thus we get the pair of values (0,0), (,0) and (0,

        Now, we calculate

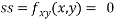
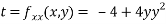
        At the point (0,0)

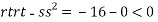
       So function has saddle point at (0,0).

       At the point (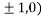

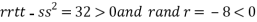
         So the function has maxima at this point (.

        At the point (0,

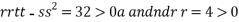
       So the function has minima at this point (0,.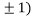

        At the point (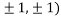

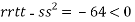
        So the function has an saddle point at (