Unit 2

Wave packet and Wave equation

1. Derive Relation between group velocity and phase velocity.

For a wave group formed by the superposition of number of waves, the group velocity and phase velocity are given by

For any propagating wave packet –

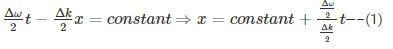
Velocity is the rate of change of displacement given by--

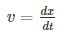
Hence, group velocity is got by differentiating equation (1) with respect to time…

We know that phase velocity is given by

Substituting?? = kVp in equation (2) we get-

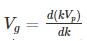
Thus, we arrive at the equation relating group velocity and phase velocity –

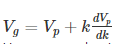
2.     Explain Heisenberg’s uncertainty principle.

Statement: It is impossible to determine simultaneously both the position and momentum of a quantum mechanical particle moving inside the wave packet with equal accuracy. In any simultaneous determination of the position and momentum of a particle, the product of the corresponding uncertainties inherently present in the measurement is equal to, greater than (h/4π).

Explanation: Consider a quantum particle moving inside a wave packet of width Δx. Then inside the wave packet it is not possible to find the exact position of the particle and any attempt to measure it will have an uncertainty (error) which less than or equal to Δx.

The maximum uncertainty involved in measuring the position of the particle within the wave packet is Δx. Since position cannot be measured accurately, there will be an uncertainty in measuring momentum also. According to Heisenberg’s uncertainty principle, the product of uncertainty involved in the measurement of these two quantities is given by the relation,

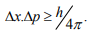
Where ∆x = uncertainty in position.

            ∆p = uncertainty in momentum.

It can be applied to any conjugate physical quantities such as energy and time, angular position and angular momentum etc.

Other forms of Uncertainties are:

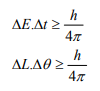
Where, ΔE, Δt are the uncertainties in the measurement of energy and time, and ΔL, Δθ are the uncertainties in the measurement of angular momentum and angular position.

3.    Explain Wave function and its probability interpretation.

The quantity that characterizes the de–Broglie wave or matter wave is called the wave function. It is usually denoted as Ψ = (x, y, z, t). This gives complete information about the state of a physical system at a particular time.

It is also called the state function and represents the probability amplitude. If ‘Ψ’ is large, the probability of finding the particle is also large and if ‘Ψ’ is small then the probability of finding the particle is small. The wave function gives the likelihood of finding the particle at a given instant and at a given position inside the wave packet.

Properties of wave functions:

There are certain properties that an acceptable wave function ‘Ψ ‘must satisfy:

1. In order to avoid infinite probabilities, Ψ must be finite for all values of x, y, z.

2.     In order to avoid multiple values of the probability, Ψ must be single valued. i.e., for each set of x, y and z, Ψ must have a unique value.

3.     For finite potentials, Ψ and 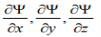must be continuous in all regions.

4.     In order to normalize the wave function, Ψ must approach to zero as ‘x’ approaches to ± infinity.

In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’ . Thus, Ψ2 is a measure of particle density.

According to Max Born ΨΨ* = |Ψ|2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume dv (= dxdydz) is given by |Ψ|2 dv or |Ψ |2 dx.dy.dz.

Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space.

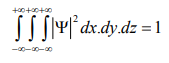             or

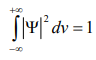
This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function.

5.     State and explain Schrödinger’s Time dependent & time independent equations.

Time dependent equation:

It was observed that the wave function of a particle of fixed energy E could most naturally be written as a linear combination of wave functions of the form:

Now the hemiltonian of this system:

            H=T+V

Where V is the potential energy and T is the kinetic energy. As we already know that ‘H’ is the total energy, we can rewrite the equation as:

Now taking the derivatives:

We know that:

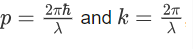
Where ‘λ’ is the wavelength and ‘k’ is the wavenumber.

We have:

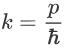
Therefore:

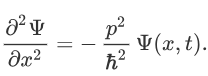
Now multiplying Ψ (x, t) to the Hamiltonian we get:

The above expression can be written as:

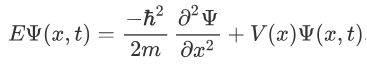
We already know that the energy wave of a matter wave is written as:

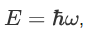
So, we can say that

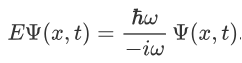
Now combining the right parts, we can get the Schrodinger Wave Equation.

Time independent equation:

According to de-Broglie theory, for a particle of mass ‘m’, moving with a velocity ‘v’, the wavelength associated with it is

             λ=h/p

The wave equation for a de-Broglie wave can be written in complex notation as:

           …………1

Where, A is the amplitude, ω is angular frequency and k is the wave vector.

Differentiate equation (1) with respect to ‘t’ twice, we get

We have differential equation for the traveling wave as,

                ……….3

Where, y is displacement and ‘v’ is velocity of wave.

By analogy, we can write the wave equation for de-Broglie wave associated with the motion of a free particle as,

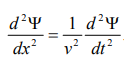             ………4

This represents the de-Broglie wave propagating along x-direction with a velocity ‘v’ and ‘Ψ’ is the displacement.

From equation (2) and (4),

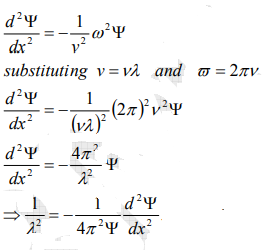          …………..5

The kinetic energy of a moving particle of mass ‘m’ and velocity ‘v’ is given by

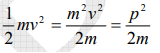
But we have from equation (1), p = (h/λ)

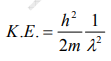
Substitute for (1/ λ)2 from equation (5),

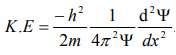       …………….6

Let there be a field where the particle is present. Depending on its position in the field, the particle will possess certain potential energy. Then we can write:

Total energy = Kinetic energy + Potential energy

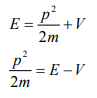
From equation (6), we can write

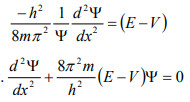
This is the time independent Schrödinger’s wave equation in one-dimension.

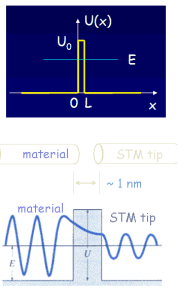
6.    Find a Solution of Schrödinger’s equation for one dimensional infinite potential well.

We will now look at the solutions of a particle of mass m confined to move along the x-axis between 0 to L. This is achieved by making the potential 0 between x = 0 and x = L and V = ∞ for x < 0 and x > L. In quantum mechanics this model is referred to as particle in a box (PIB) of length L.

The one-dimensional infinite potential well of length L. It is divided into three regions, with regions I and III having V = ∞ and region II having V = 0

Before we set up and solve the Schrodinger equation let us apply de Broglie’s approach to this problem. De Broglie associates a wave with every material particle traveling with momentum p. The wavelength of the wave is

The classical analog of a particle in a box is a string that is fixed at both ends. When such a string is plucked, we know that the amplitude of the oscillations at the fixed ends is zero. In other words, an integer number of half-wavelengths must fit in the length of the box. Applying this idea to the present case, we find that

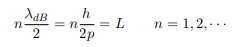
Solving for p we get

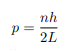
The particle feels no potential energy so all its energy is in the form of kinetic energy. As a result

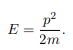
Substituting for p, we get

The Schrodinger equation is-

Hψˆ (x) = Eψ(x)

Where V (x) = ∞ in regions I and III and V (x) = 0 in region II. The results are in no way affected if in region II the potential is V because it only has the effect of altering the zero of energy and so without of generality, we will assume that V = 0 within the box. In regions I and III the wave function is identically zero since the potential is infinite so we will only have to consider the solution within the box. We are looking for the solutions to the equation.

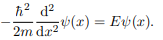
We rewrite this differential equation in the form:

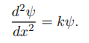
Wave equation

          ψ(x) = A cos(kx) + B sin(kx)

The boundary conditions that the wave function should satisfy are

 ψ (0) = 0 and ψ(L) = 0. The

First of these conditions implies that A = 0.

The second condition yields

B sin(kL) = 0

Which implies that kL = nπ, n = 1, 2, 3, · · ·

Or in other words k = nπ/L. Because E is related to k we hence obtain that

You will notice that the application of the boundary conditions naturally leads to quantization. In addition, observe that we do not consider n = 0 as a possibility because that would imply that the wave function is identically zero for all x or in other words there is no particle! The constant B is yet to be determined. The normalization condition on the wave function yields B.

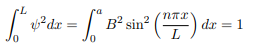
In cases where the wave function is not an eigen function of the operator corresponding to the observable, we will be concerned with the statistical mean of the measured values, averaged over a large number of measurements, the expectation value. The expectation value is defined of an operator is defined a: 

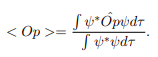
 The average momentum is the

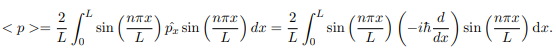
7.    Explain Barrier Tunneling.

In quantum mechanics the solutions in the classically forbidden regions are exponentially decaying solutions, and they fall to zero rapidly.  But if the region in which the kinetic energy is negative is narrow, then it is possible for the exponential solution to smoothly connect two oscillating solutions on both sides of the region, and for the particle to have a finite probability of presence in that region.  This leads to the phenomena of barrier penetration and tunneling.

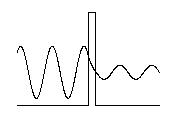
Tunneling in two dimensions:

We can consider the surface of a metal as a two-dimensional system.  Electrons cannot escape, but due to “barrier penetration”, the electron density of a metal actually extends outside the surface of the metal.  The distance x outside the surface of the metal at which the electron probability density drops to 1/1000 of that just inside the metal is on the order of 0.1 to 1 nanometer

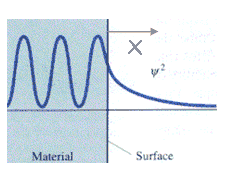
The transmittance T is the probability that an electron will tunnel through a barrier.  The transmittance T is approximately given by the simple exponential form T = exp(-2bL) with b = (2m(U0-E)/ħ2)1/2.  T depends on the difference of the electron energy E and the height of the barrier U0, and on the barrier width L.  For a metal (U0-E) is approximately equal to the work function of the metal.

Tunneling in three dimensions:

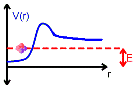
Let us consider alpha decay.  The nucleus decays by emitting an alpha particle.  An alpha particle is a Helium nucleus consisting of two protons and two neutrons.

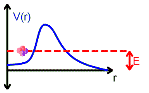
The alpha particle is trapped inside the nucleus in a potential well.  But the well walls do not extend to infinity.  If the shape of the well is of the form shown in the figure above, then there is a finite chance that he alpha particle can tunnel through the potential barrier.  The decay of an nucleus via alpha decay takes a long time if the barrier is high and thick.  Some nuclei, like lead, are considered stable but may have lifetimes greater than the age of the universe.  If the barrier is not very high and narrow, alpha decay can happen very rapidly.  If the shape of the barrier, however, is of the form shown in the figure below, then the alpha particle cannot tunnel through the barrier and the nucleus is stable against alpha decay.