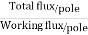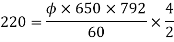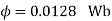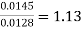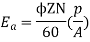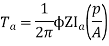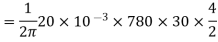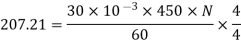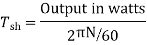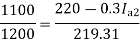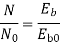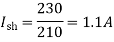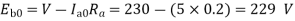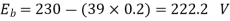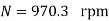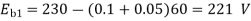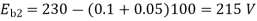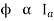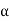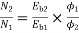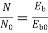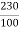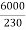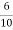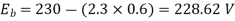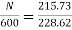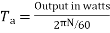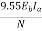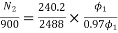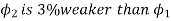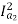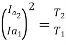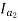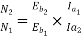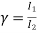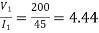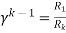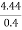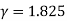A 250V shunt motor on no load runs at 900rpm and takes 4amperes armature and shunt field resistances are 0.2 and 250 ohms respectively. Calculate the speed when loaded taking current of 50A. The armature reactions weaken the field by 3

AEE

Unit – 2DC Machines Q1) A 4 pole dc generator runs at 650 rpm and generates emf of 220V. The armature is wave wound and has 790 conductors. If total flux/pole is 0.0145 Wb in each pole, find leakage coefficient. A1)

Leakage coefficient =

Working flux is given as

A = 2 for simple wave winding.

Leakage coefficient =

Q2) A 4 pole lap wound dc shunt generator has a useful flux per pole of 0.05 Wb. The armature winding consists of 200 turns each of 0.06 u ohm resistance. Calculate the terminal voltage when running at 900 rpm with armature current of 50 A. A2)

Terminal voltage V =Ea – Ia Ra

Ia Ra = 50×Ra.

Z = 200×2=400 (each turn has two sides).

N = 900 rpm = 0.05 Wb P = A = 4

Total resistance of 200 turns = 200 × 0.004 = 0.8 ohm

As there are 4 parallel paths, so resistance of each path = 0.8/4 = 0.2 ohm

There are 4 resistances in parallel of each of 0.2 ohm

Ra = 0.2/4 = 0.05 ohm

Ia Ra = 50×0.05 = 25 V

V = Ea – Ia Ra = 300 – 25 = 275 V

Q3) A 220 V 4 pole wave wound dc series motor has 780 conductors on its armature. It has armature and series field resistance of 0.75 ohm. The motor takes a current of 30A. Find the speed and gross torque developed if flux/pole is 20 mWb? A3)

Back emf,

Eb = V – IaRa = 220 – (30×0.75) = 197.5 V

197.5 = 20 × 10-3 ×780×N×0.75

N = 16.88 ≈ 17

Ta = 158.97 Nm.

Q4) A 4 pole, 210 V shunt motor has 450 lap wound conductor. It takes 32 A from supply mains and develops output power of 4.5 kW. The field takes 1 A. The armature resistance is 0.09 ohm and flux per pole is 30 mWb. Calculate speed and torque. A4)

) Ia = 32-1 = 31 n

Eb = V – Ia Ra = 210 - (0.09×31) = 207.21 V

N = 920.9 rpm

Q5) A 220 V, dc shunt motor has an armature resistance of 0.3 ohm and field resistance of 105 ohm. At no load speed is 1200 rpm and armature current is 2.3 A on application of rated load speed drops to 1120 rpm. Find the current and power input when motor delivers rated load. A5)

) N1 = 1200 rpm Eb1 = 220 – (0.3×2.3) = 219.31 V

N2 = 1120 rpm Eb2 = 220 – 0.3 Ia2

Ia2 = 37.93 A

Line current = Ia2 + Ish = 37.93 + (220/105) = 40 A

Power input = 220 × 40 = 8800 W

Q6) A 230 V shunt motor runs at 1000 rpm at no load and takes 6A. The total armature resistance is 0.2 ohm and field resistance are 210 ohms. Calculate the speed when loaded and taking 40 A. Assume flux constant. A6)

Q7) The armature resistance of a 15 kW, 230 V series motor is 0? 1 ohm, the brush voltage drop is 3 V and series field resistance is 0.05 ohm. The motor takes 60 A speed is 600 rpm. Calculate speed when current is 100 A. A7)

Φ1 60

Φ2 100

N2=350.22 rpm

Q8) A 230V DC Shunt motor takes 4A at no load when running at 600 rpm. The field resistance is 100 ohms. The resistance of armature at standstill gives a drop of 6V across armature terminals when 10A were passed through it. Find i) Speed at no load (ii) Torque. Normal input of motor is 6kW A8)

i)Speed

Ish= =2.3A

F.L Power=6000

F.L line current= =26.08A

Ia=26.08-2.3=23.78A

Ra==0.6Ω

N=566.2 rpm

ii)Torque Ta= =

Q9)

A 250V shunt motor on no load runs at 900rpm and takes 4amperes, armature and shunt field resistances are 0.2 and 250 ohms respectively. Calculate the speed when loaded taking current of 50A. The armature reactions weaken the field by 3%?A9)

Ish=250/250=1A

Ia1=4-1=3A

Ia2=50-1=49A

Eb1=250-3*0.4=248.8V

Eb2=250-49*0.2=240.2A

N2=898rpm

Q10) The speed of a 37.3kW series motor working on 500V supply is 600 rpm at full load and 90% efficiency. If the load torque is made 250 N-m and a 5ohm resistance is connected in series with the machine, calculate the speed at which the machine will run. Assume armature and field resistance of 0.5ohm?A10)

Load torque in first case T1=37300/2(600/60) =593.65 N-m

Input current Ia1=37300/0.9*500=82.9A

T2=250 N-m. So, finding Ia2

For series motor T α φ Ia α Ia2

T1 α and T2 α

=82.9*=53.79A

Eb1=500-(82.9*0.5) =458.5V

Eb2=500-53.79(5+0.5) =204.11V

Q11) A starter required for a 220V shunt motor. The maximum allowable current is 45A and the maximum current is about 35A. Find the number of sections of starter resistance required and the resistance of each section. The armature resistance of motor is 0.4 ohm?A11)

I1=45 A, I2=35 A

=1.28

R1=Ω

==11.1

As we already know

R1=4.44Ω

R2=

R3=

r1= R1- R2=2.01

r2= R2- R3=1.1

Similarly, r3=0.60, r4=0.20 can be calculated.

Sign Up