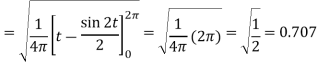Unit - 1
Integral calculus-I
Q1) What is beta function?
A1)
The beta and gamma functions are defined as-

And

These integrals are also known as first and second Eulerian integrals.
Note- Beta function is symmetrical with respect to m and n.
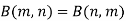
Q2) Evaluate dx
dx
A2)
 dx =
dx = 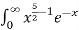 dx
dx
= γ(5/2)
= γ(3/2+ 1)
= 3/2 γ(3/2 )
= 3/2. ½ γ(½ )
= 3/2. ½ π
= ¾ π
Q3) Find γ(-½)
A3)
(-½) + 1= ½
γ(-1/2) = γ(-½ + 1) / (-½)
= - 2 γ(1/2 )
= - 2 π
Q4) Evaluate 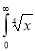
 dx.
dx.
A4)
Let 
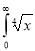
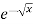 dx
dx
Put 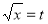 or
or  ;dx =2t dt
;dx =2t dt
X | 0 |  |
t | 0 | 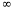 |
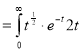 dt
dt
 dt
dt
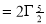
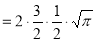
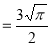
Q5) Evaluate beta function.
A5)
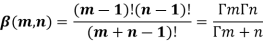
Here we have-
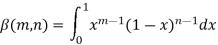
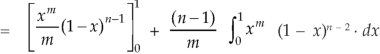
Or
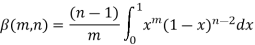
Again integrate by parts, we get-
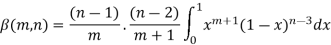
Repeating the process above, integrating by parts we get-
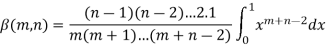
Or
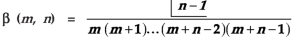
Q6) What is the relationship between beta and gamma function.
A6)
We know that-
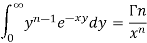
 ………… (1)
………… (1)
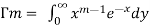 …………………..(2)
…………………..(2)
Multiply equation (1) by  , we get-
, we get-
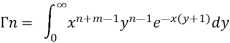
Integrate both sides with respect to x within limits x = 0 to x = 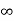 , we get-
, we get-
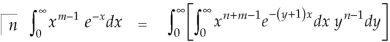
But
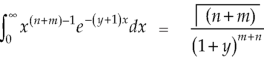
By putting λ = 1 + y and n = m + n
We get by using this result in (2)-
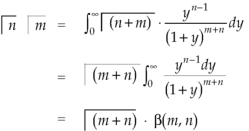
So that-
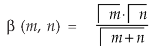
Q7) Evaluate I = 
A7)
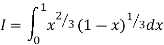
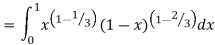
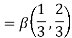
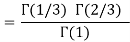
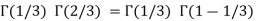
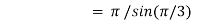
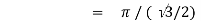
= 2 π/3
Q8) Prove that-
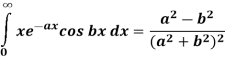
Where a>0.
A8)
We know that-
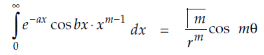
Put m – 1 = 1 or m = 2
We get-
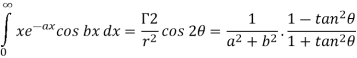

Hence proved
Q9) Evaluate
A9)
Let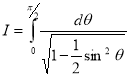
Put 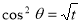 or
or 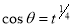 ,
,
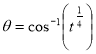 ,
,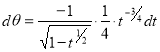
When ,
,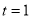 ;
; ,
,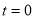
 | o | 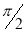 |
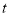 | 1 | 0 |
Also
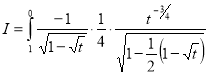
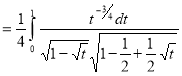
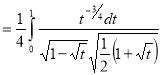
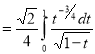

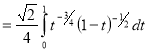


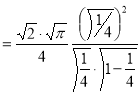

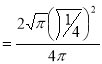

Q10) What is elliptical integral?
A10)
The integral 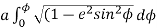 is called elliptic function.
is called elliptic function.
This is derived from the determination of the perimeter of the ellipse.
To evaluate this integral, we first expand the integrand 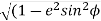 as power series and then integrate term by term.
as power series and then integrate term by term.
Elliptic integral of first kind
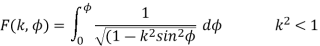
Elliptic integral of second kind
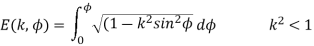
Here k is modulus and  is amplitude.
is amplitude.
Q11) Express  in terms of elliptic integral.
in terms of elliptic integral.
A11)
Here we have-
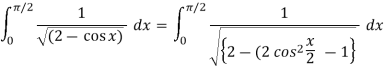
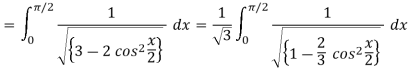
Put 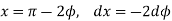
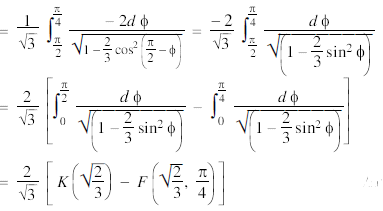
Q12) What is error function?
A12)
Error function of x is written as erf(x) and defined as below-
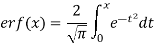
The complementary function of error function of x is written as 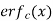 and defined as below-
and defined as below-

Note-
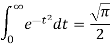
Q13) Find erf(0).
A13)
We know that-
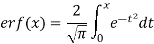
Then

Hence-
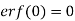
Q14) Prove that erf (-x) = - erf (x)
A14)
We know that-
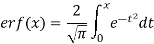
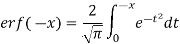
Put t = -u

Q15) Find the mean value of f(t) = 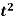 over the interval
over the interval 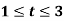
A15)
As we know that
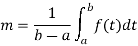
Here
a = 1 and b = 3 and f(t) = 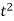
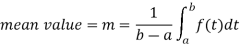

Q16) What do you understand by Root-mean-square-value of a function?
A16)
If f(t) is defined on the interval 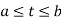 , the mean-square value is given by the expression:
, the mean-square value is given by the expression:
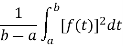
This is simply the mean value of  over the given interval.
over the given interval.
The related quantity: the root-mean-square (r.m.s.) value is given by the following formula.
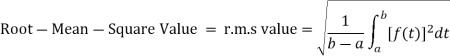
The r.m.s. Value depends upon the interval chosen. If the values of a or b are changed, then the r.m.s. Value of the function across the interval from a to b will in general change as well. Note that when finding an r.m.s. Value the function must be squared before it is integrated.
Q17) Find the r.m.s value of f(t) = sin t across the interval 
A17)
Here a = 0 and b = 2_ so r.m.s can be calculated as,
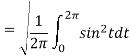
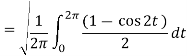
Note-