Unit - 3
Solution of First and Second order Networks
Q1) V0 (t) = ? t =o if capacitor is uncharged?
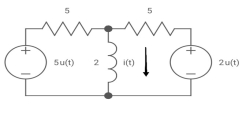
A1) We know i(t) = i( )+[ i(0)- i(
)+[ i(0)- i(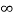 )]
)]
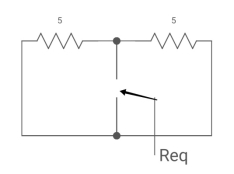
Fig 1 Finding Req
Req = R1R2 /R1+R2=(5x5)/(5+5)=5/2ohm
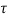 =L/Req=4/5 sec
=L/Req=4/5 sec
i(0)=0
i( )=u(t)+
)=u(t)+ u(t)=1.4u(t)
u(t)=1.4u(t)
i(t)=1.4[1-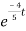 ]u(t)
]u(t)
Q2) Find Vo(t) for the circuit below?
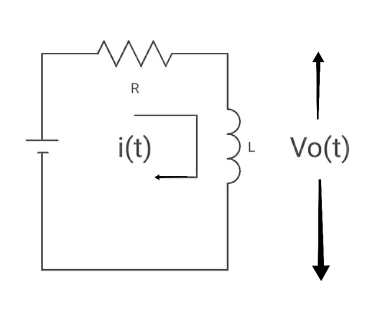
A2)
Time constant 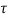 =L/Req = L/R
=L/Req = L/R
V ( ) = 0, V (0) =VR (supply voltage)
) = 0, V (0) =VR (supply voltage)
i ( ) = VR/R, i(0) =0
) = VR/R, i(0) =0
By KVL,
VR=i(t) R + L di/dt(t)
On solving
V0(t)= VR e-tR/L
Q3) In network below switch is moved from 1 to 2 at t=0 a steady state is achieved already. Fond capacitor voltage Vc(t) and current i(t) through 200Ω?

Fig 2. Circuit Diagram
A3) The Voltage across capacitor is given by
Vc(t)= K1+K2 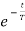
The steady state is reached when t=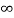 the above equation becomes
the above equation becomes
Vc( )= Lt t-->
)= Lt t-->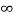 K = K1
K = K1
At t=0
Vc(0)= K1+K2
K2= Vc(0)- Vc( )
)
The final response for the circuit is given as
Vc(t)= Vc( )-[Vc(
)-[Vc( )-Vc(
)-Vc( )]
)]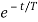
When switch is at position 1
Vc(0)= 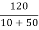 x 50 = 100V
x 50 = 100V
So, voltage of capacitor at t=0 and t=0+ will remain same.
TO find Req we replace voltage source by short circuit
Req = 60||200||50 = 24 Ω
The time constant will be T = ReqC = 24x0.05 = 1.2sec
Switch at position 2
The steady state voltage across capacitor is given by
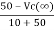 =
=  +
+ 
Vc( ) = 20V
) = 20V
The complete response will be
Vc(t)= Vc(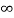 )-[Vc(
)-[Vc(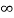 )-Vc(
)-Vc( )]
)]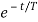
Vc(t)= 20 –[20-100]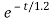
Vc(t)= 20+ 80 
The value of current at switch position 1
I= 50/(200+60) = 0.192A
When switch is at 2
i(0+) = 100/200= 0.5A
i(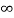 ) = Vc(
) = Vc(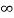 ) /200 = 0.1A
) /200 = 0.1A
The complete response of current is
i(t)= i(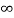 )-[i(
)-[i(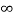 )-i(
)-i(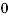 )]
)]
i(t)= 0.1-[0.1-0.5]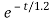
i(t)=0.1+0.4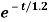
Q4) Find the value of V0(t) for circuit below?

A4)
Time constant, c= L/Req = L/R
V( ) = 0
) = 0
V(0) = VR
i( ) = VR/R
) = VR/R
i(0) =0
By KVL,
VR=i(t) R + L di/dt(t)
On solving
V0(t)= VR e-tR/L
Q5) Find iL(t) for the circuit below. For t>0?
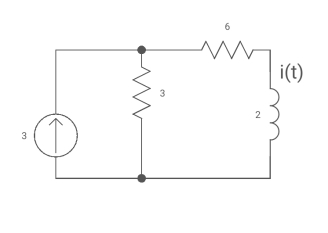
A5)
The circuit for Req will be
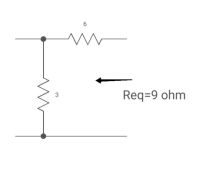
Fig 3. Circuit for Req
Req = 6+3
= 9ohm
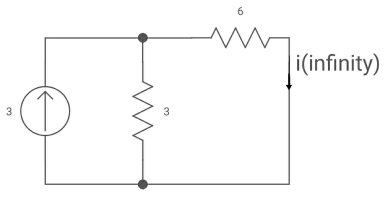
Fig 4. Circuit when inductor acts as short circuit
T= L/Req = 2/9 sec
i(0) =0
i( ) = 3*3/6+3 = 1A
) = 3*3/6+3 = 1A
i(t) = 1 [1-e4.5t]
Q6) Capacitor is initially uncharged find Vc (t); t >0
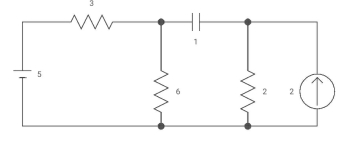
Fig 5. Circuit Diagram
A6)

Fig 6. Circuit for Req
Req = (3116)+2
=2+2 = 4ohm
T= C Req= 2 sec
Clearly Vc(0) =0
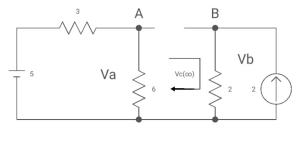
Fig 7. Circuit when capacitor acts as open circuit
By voltage divides, VA = 5*6/3+B = 30 v/9
Clearly by ohms low
VB = 2*2 = 4v
Apply KVL, VA-Vc-VB =0
Vc(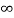 ) = 30/9 – 4 = -2/3 V
) = 30/9 – 4 = -2/3 V
Vc (t) = -2/3 [1- e0.25t]
CURVE:
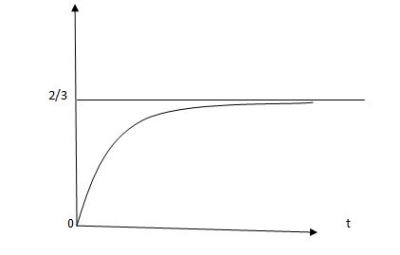
Vc(t) =2/3 [1-e-0.5t]
Fig 8 Response for above circuit
Vc(t) = -2/3 [1-e-0.5t]
Q7) Find i(t) for the given circuit below?
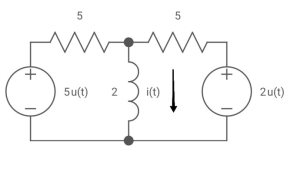
A7)
We know i(t) = i ( ) +[i(0)- i(
) +[i(0)- i(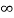 )] e-t/T
)] e-t/T
Fig 9. Circuit for Req
Req = 5*5/5+5 = 5/2 ohm
T=L/Req = 4/5 sec
Also
i(0) =0
i( ) = u(t) +2/5 u(t)
) = u(t) +2/5 u(t)
i(t) = 1.4 [1-e-5/4t)]u(t)
Q8) If switch ‘s’ closed for long time before opening at t=0-. Find Vx (0+)?
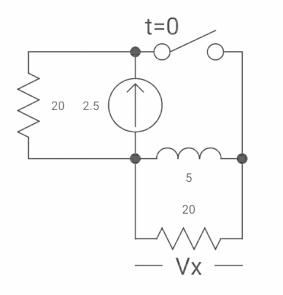
Fig 10. Circuit diagram
A8) At t= 0- switch was closed,
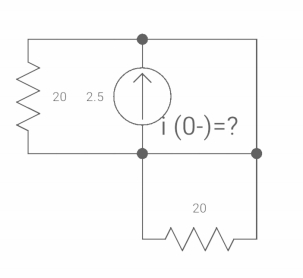
Fig 11. Switch is open
iL(0-) = 2.5A
At t= 0+
Inductor is initially charged so iL(0-) = iL(0+)
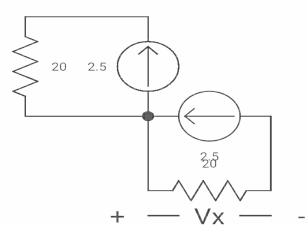
Fig 12. When switch is closed for long
-Vx = 20x2.5
Vx = -50A
Q9) Find VR(0+) and dil/dt(t) = 0+ If switch is opened at t= 0?
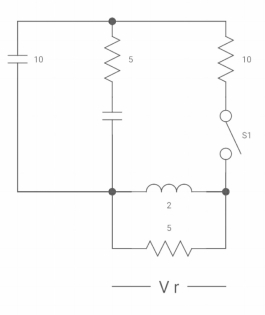
A9)
At time t=0-
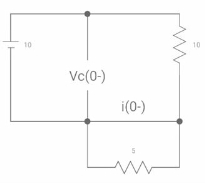
Fig 13. Capacitor SC switch closed for long
At t=0-
Vc(0-) = 10V
IL(0-) = 10/10 = 1 A
Also, iL(0-) = iL(0+) = 1A

VR(0+) = 5V
Ldi(t)/dt = VL (t)
DiL(t)/dt = VL(t)/L
At t= 0+
d iL (0+) /dt = VL(0+)/L
-VL (0+)-VR =0
VL (0+) = -5V
DiL(t)/dt at t=0+
VL(0+)/L =-5/2
Dil/dt(o+) = 2.5 A/s
Q10) Find Vc(o+) and iR (o+) it switch‘s’ is closed at t=0?
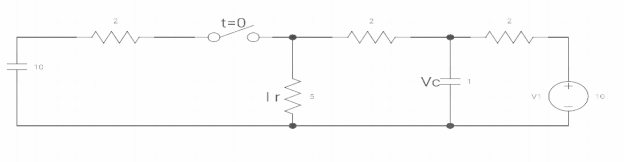
A10) At t=0-
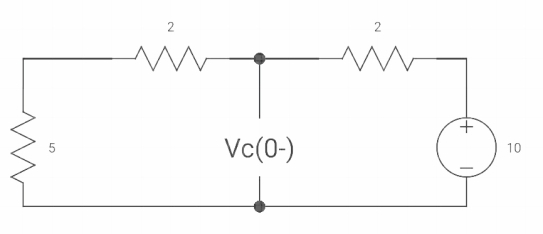
Fig 14. When switch opened at t=0
As capacitor is fully charged so acts as open circuit
Vc (0-) = 7*10/7+2 = 70/9v
At t=0+
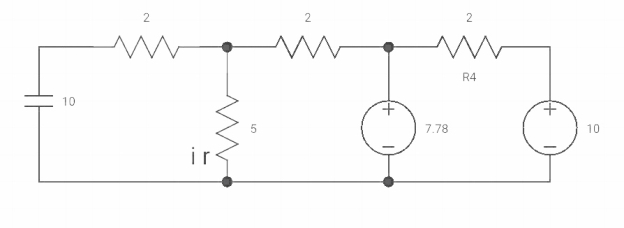
Fig 15. At t=0+ circuit
Vc(0+) = Vc (0) = 40/9v
By applying kcl at A,
VA-10/2+ VA/5+VA-7019/2 =0
VA [1/5+1/2+1/2] = 5+35/9
Va [6/5] = 80/9
Va= 400/54v
IR (0+) = Va/5 = 400/54*5 = 80/54 A
Q11) Find diL(t)/dt and dVc(t)/dt at t=0+. If switch is opened at t=0?

A11)
At t=0-
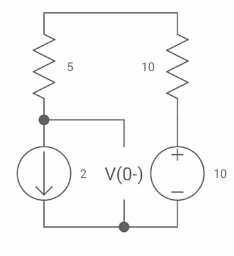
Fig 16. Switch closed for long
Vc(0-) =10V = Vc(0+)
iL(0-) = 2A
DiL(t)/dt = VL(t)/L
At t=0+
DiL(0+)/dt = VL(0+)/L
Similarly, C = ic(t)
= ic(t)
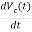 = ic(t)/C
= ic(t)/C
At t=0+
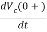 = ic(0+)/C
= ic(0+)/C
ic(0+) = -2A
Q12) Find whether the following network function represent the driving point function.
a) f(s)= (s+1)/(s2+1) b) f(s) = 3s2+2s+1/ss3+9s2+3s+2 c) f(s)=(s2+1)2/s2(s+3)
A12)
a) f(s)=s+1/s2+1
It represents the driving point function:
b) F(S)= 3S2+2S+1 / 5S3+9S2+3S+2
It represents the driving point function.
c) f(s) = (s2+1)2/s2(5+3)
It has representative zeros, hence not valid
(s2+1)2=0
s2=+-1
s2=+-j,+-j
Q13) For network below 1), pole - zero pattern is represented in fig 2) , find numerical value of R,L and c for z (0)=1?
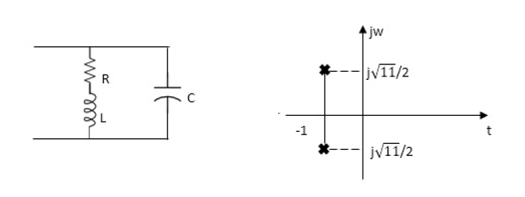
A13)
Calculating z(s) by taking L.T of fig 1)
z(s) = (R+SL)*1/CS
(R+SL)+1/CS = R+SL / SRC+S2LC+1
Z(S)= S+R/L / C [S2+R/L S+1/LC]
Given z(0)=1
z(0)=R/L / C/LC =1
Z(0)=R=1
.: R=1
Polls are given as
S2+RS/L+1/LC=0
S=-R/2L +J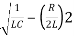
Zeros are given as
S+R / L=0
From pole zero plot value of pole location is at -1 so
-R / L = -1
-1/ L=-1
L=1H
Also imaginary part of pole from plot is
 =
=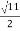
1/LC-(R/2L)2 =11/4
1/C-(1/2)2=11/4
1/C-1/4=11/4
1/C=11/4+1/4
1/C=12/4 =3
C=1/3 F
Hence, value of R=1 L=14 and c=1/3 f
L=14 and c=1/3 f
Q14) FOR the following circuits, FIND G12(S) =v2/v1?

A14)
Taking Laplace transform of above we have
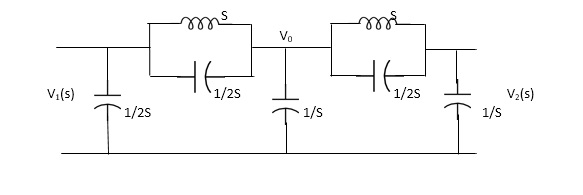
Applying KCL at node v0
V0-V1(S) / S*1/2S/(S+1/2S) +V0+V2(S)/ (S*1/2S)/(S+1/2S)+V0/1/S=0
For Porr 2)We have,
v2-v0/(s*1/2s)/(s+1/2s)+v2/1/s =0 ---------(ii)
(v2-v0)(2s2+1) / s +sv2=0
v2 [2s2+1/s+s] = v0( 2s2+1)/ s
v0=v2(3s2+1) / (2s2+1)-----------(iii)
From (i) we have,
(v0-v1) /s (2s2+1) *sv0+(v0-v2)/5 (s2+1) =0
(2s2+1/5)v0-(2s2+1)/sv1+sv0+(2s2+1)/sv0-(s2+1)/s v2=0
(2s2+1)v1=(5s2+2)v0-(2s2+1)v2
Substitute value v0 from (iii) above
(2s2+1)v1 =[( 5s2+2)(3s2+1) /(2s2+1)-(2s2+1)]v2
(2s2+1)v1=(15s4+5s2+6s2+2-4s4+4s2) / (2s2+1 *v2
G12(s) = v2/v1 = (2s2+1) 2/11s4+15s2+1
Q15) Find the transfer function admittance ratio
Y12(s) = I2(S) / V1(S)

A15)
Taking Laplace transform of above figure

Applying KCL we get,
(V2-V1) / (3*1/2S) / (3+1/2S) * V2/ 1/2S+ V2/1/6 =0
(Y2-V1)(6S+1) / (6S+4) * (2S+6)V2V=0
BUT I2=-6V2
V2=-I2/6
We have,
(6s+1) / (6s+4)*v2-(6s+1) / (6s+4)*v1 +(2s+6)v2=0
-[6s+1 / 6s+s+2s+6]I2 / 6 =V1(6S+1) / 6S+4
-[6S+1(2S+6)(6S+4)]I2= 6(6S+1)V1
-[(6S+1)*12S2+36S+8S+24] I2=6(6S+1)
I2 / V1 =-6(6S+1) / 12S2+50S+25
Y12(S) = I2(S) / V1(S) = -6(6S+1) / 12S2+50S+25
Q16) Find overall Y-parameter?


A16)
V1 – I1R – V2 = 0
V1 – V2 = I1R
I1 =  V1 -
V1 -  V2
V2
V2 = I2R + V1
I2 = -  V1 +
V1 +  V2
V2
Y11 = 
Y12 = Y21 = 
Y22 = 
Q17) Find overall Y-parameter

A17)
Y-parameter does not exist as V1 = V2
Q17) Find overall Y-parameter?
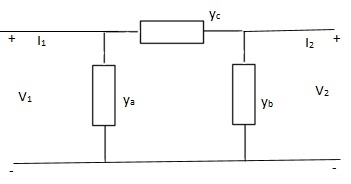
A18)
I1 = V1Ya + (V1 – V2)Yc
I1 = (Ya + Yc)V1 - YcV2
I2 = V2Yb + (V2 – V1)Yc
I1 = (Yb + Yc)V2 - YcV1
Y11 = Yb + Yc
Y12 = Y21 = - Yc
Y22 = Yb + Yc
Q18) Find overall Y-parameter?
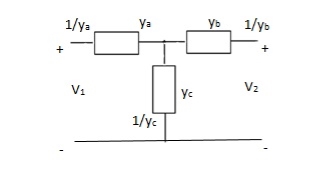
A19)
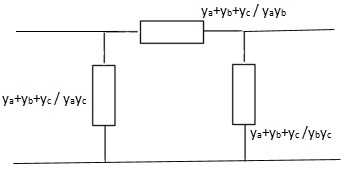

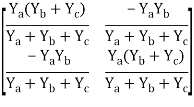
Q19) Find Z11, Z12, Z22, Z21?
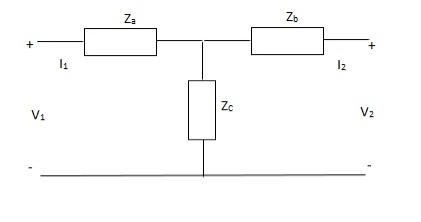
A20)
V1 = I1Za + I1Zc + I2Zc
= (Za + Zc)I1 + ZcI2
V2 = I2Zb + I2Zc + I1Zc
= (Zb + Zc)I1 + ZcI1
Z11 = (Za + Zc)
Z12 = Zc = Z21
Z22 = (Zb + Zc)
Q20) Find all z-parameters?

A21)
V1 = Za(I1 - I)
(I - I1)Za+ IZc+ Zb(I + I2) = 0
I(Za + Zb + Zc) – I1Za + I2Zb = 0
I = 
V1 = ZaI1 - Za
= 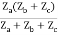 I1 + I2
I1 + I2 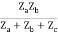
V2 = Zb(I2 + I)
= ZbI2 + Zb
=  I2 + I2
I2 + I2 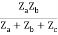
Z11 = 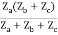
Z12 = Z21 = 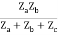
Z22 = 
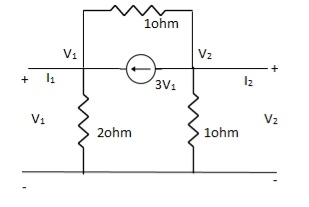
Q21) Find all the Transmission parameters?
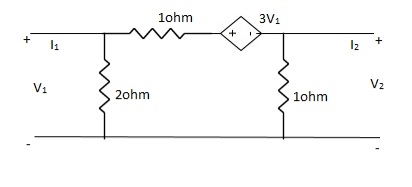
A22)
-3V1 – I1 +  +
+ 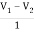 = 0
= 0
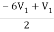 +
+  = I1
= I1
 V1 – V2 = I1
V1 – V2 = I1
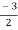 V1 = V2 + I1
V1 = V2 + I1
V1=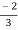 V2-
V2- 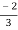 I1----------------(1)
I1----------------(1)
I2 = 3V1 + V2 + V2 – V1
I2 = 2V1 + 2V2
2V1 = I2 - 2V2
2V1 = - 2V2 + I2
V1 = -V2 +  I2 ----------------(2)
I2 ----------------(2)
A = -1
B = 
From (1) & (2)
-V2 +  I2 =
I2 = 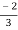 I1 -
I1 -  V2
V2
 V2 - V2 +
V2 - V2 +  I2 =
I2 = 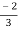 I1
I1
 I1 =
I1 =  V2 + V2 -
V2 + V2 -  I2
I2
I1 =  V2 -
V2 -  I2
I2
C = 
D = 
Q22) Find all the Transmission parameters?

A23)
V1 = RI1 + V2 ----------------(1)
I2R = V2 – V1
I2 =  V2 -
V2 -  V1
V1
I2R = V2 – V1
V1 = I2R - V2 --------------------(2)
A = 1
B = R
From (2) in (1)
V2 - I2R = V2 + RI1
I2 = -I1
C = 0
D = 1
Q23) Find out overall transmission parameter?

A24)


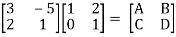

Q24) A coil takes a current of 6A when connected to 24V dc supply. To obtain the same current with 50HZ ac, the voltage required was 30V. Calculate inductance and p.f of coil?
A25)
The coil will offer only resistance to dc voltage and impedance to ac voltage
R =24/6 = 4ohm
Z= 30/6 = 5ohm
XL = 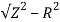
= 3ohm
Cosφ =  = 4/5 = 0.8 lagging
= 4/5 = 0.8 lagging
Q25) The potential difference measured across a coil is 4.5V, when it carries a dc current of 8A. The same coil when carries ac current of 8A at 25Hz, the potential difference is 24V. Find current and power when supplied by 50V,50Hz supply?
A26)
R=V/I= 4.5/8 = 0.56ohm
At 25Hz, Z= V/I=24/8 =3ohms
XL = 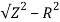
= 2.93ohm
XL = 2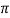 fL = 2
fL = 2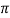 x 25x L = 2.93
x 25x L = 2.93
L=0.0187ohm
At 50Hz
XL = 2x3 =6ohm
Z = 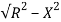 = 5.97ohm
= 5.97ohm
I= 50/5.97 = 8.37A
Power = I2R = 39.28W
Q26) A coil having inductance of 50mH an resistance 10ohmis connected in series with a 25 F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
A27)
f0= = 142.3Hz
= 142.3Hz
I0 = V/R = 200/10 = 20A
Q27) A 15mH inductor is in series with a parallel combination of 80ohm resistor and 20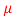 F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
A28)
XL = 2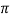 fL = 1000x15x10-3 = 15ohm
fL = 1000x15x10-3 = 15ohm
XL = 1/ C = 50ohm
C = 50ohm
Impedance of parallel combination Z = 80||-j50 = 22.5-j36
Total impedance = j15+22.5-j36 = 22.5-j21
Admittance Y= 1/Z = 0.023-j0.022 siemens
Q28) A circuit connected to a 100V, 50 Hz supply takes 0.8A at a p.f of 0.3 lagging. Calculate the resistance and inductance of the circuit when connected in series and parallel?
A29)
For series Z =100/0.8 = 125ohm
Cosφ = 
R = 0.3 x 125 = 37.5ohm
XL =  = 119.2ohm
= 119.2ohm
XL = 2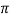 fL = 2
fL = 2 x 50x L
x 50x L
119.2 = 2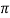 x 50x L
x 50x L
L= 0.38H
For parallel:
Active component of current = 0.8 cosφ = 0.3x0.3 = 0.24A
R = 100/0.24 =416.7ohm
Quadrature component of current = 0.8 sinφ = 0.763
XL= 100/0.763 = 131.06ohm
L= 100/0.763x2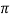 x50 = 0.417H
x50 = 0.417H