Unit 4 | unit 4 electric circuit analysis using laplace transforms

Back to Study material

Unit - 4

Electric Circuit Analysis using Laplace Transforms

Q1) Write equation for given waveform

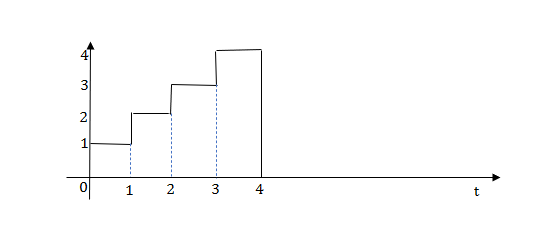
A1)

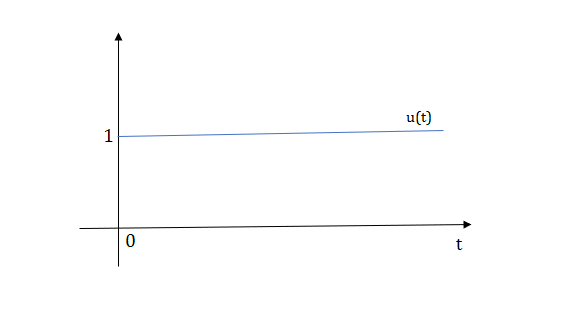
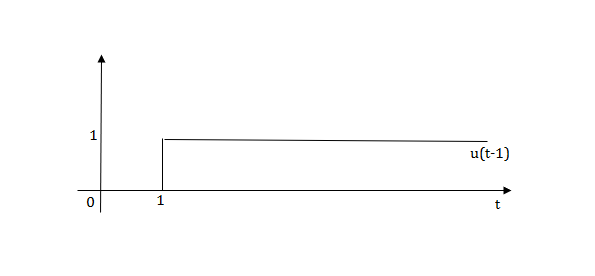
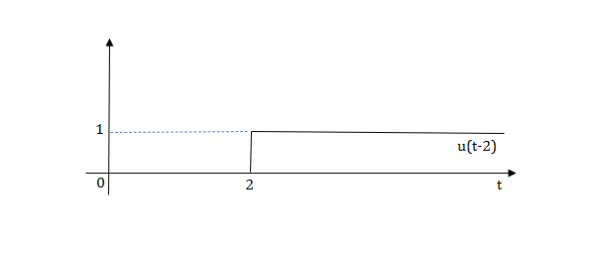
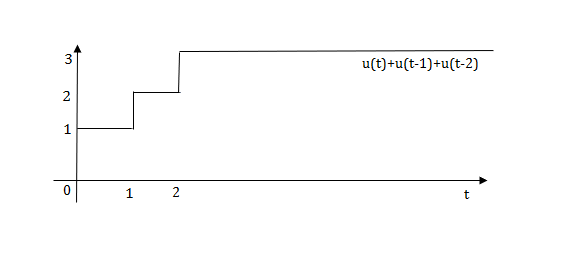
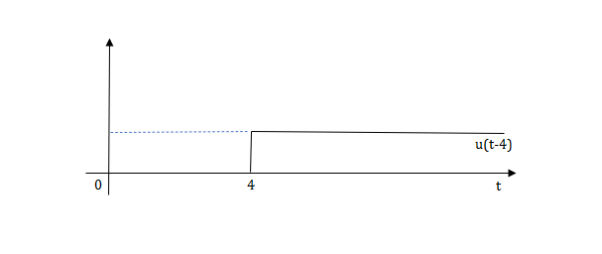
The final equation is=u(t)+u(t-1)+u(t-2)+u(t-3)-4u(t-4)

As the waveform is stopped at t=4 with amplitude 4,so we have to balance that using -4u(t-4).

Q2) Write the equation for the given waveform?

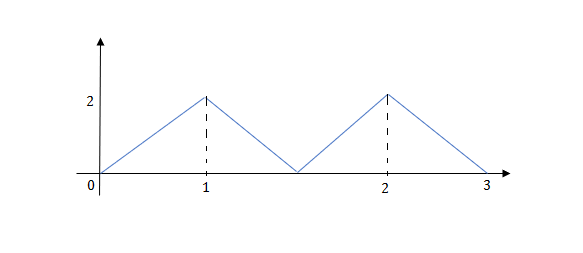
A2)

Calculating slope of above waveform

Slope for (0,0) and (1,2)

a1 slope=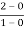=2

a2 slope=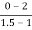=-4

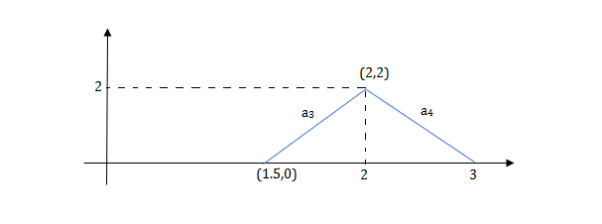
a3 slope =4 and a4= -2

At t=1 slope changes from 2 to -4 so we need to add -6r(t-1) to 2r(t) to get the slope of -4.

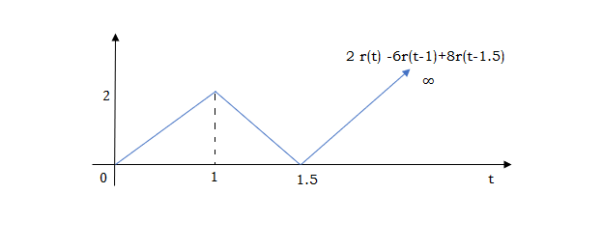
At t=1.5 slope changes from -4 to 4 so adding 8r(t-1.5) to get slope of 4

At t=2 slope changes from +4 to -2 so we add -6r(t-2). But we need to stop the waveform at t=3. Hence, we have to make slope 0. Which can be done by adding +2r(t-3). Final equation is given as 2r(t)-6r(t-1.5)+8r(t-1.5)-6r(t-2)+2r(t-3)

Q3) For given RL circuit find the differential equation for current i?

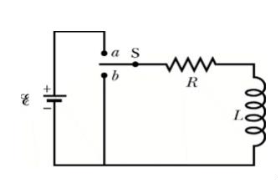
Fig. Series RL circuit

A3)

After switch is closed applying KVL

This is first order homogeneous differential equation so

Integrating both sides

Ln i= t+K

Taking antilog of both sides

i=k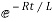

At t=0

i(0)==I0

=ke0

The particular solution is given as

i= for t≥0

=for t<0

Q4) Find IL(0) for the given circuit below

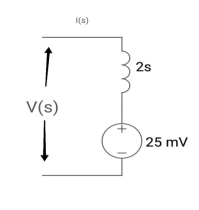
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_224139.jpg$

A4)

From above circuit

L = 2H

LiL (0) = 25 mv

IL (0) = 12.5 m A

Q5) Find value across capacitor?

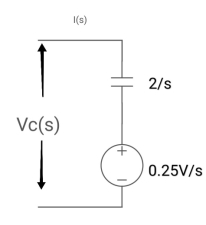
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_224353.jpg$

A5)

From above circuit we can write

1/cs = 2/s

C=1/2f

Vc (0)/s = 0.25v/s

Vc(0)= .25v

Q6) Find voltage across capacitor?

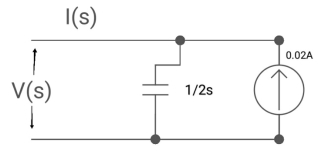
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_224735.jpg$

A6)

1/cs = 1/2S

C=2F

CVc (0) = 0.02

Vc(0)= 0.01V

Q7) For the following circuit shown below

(a) switch is at before moving to position = at t= 0, at t= 0+, i1(t) is

(a) –V/2R (b) –V/R (c) – V/4R

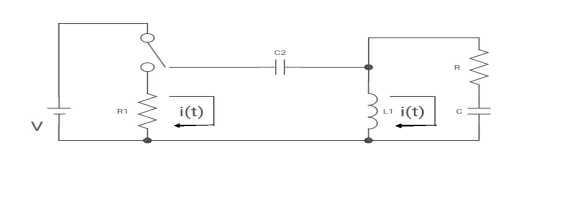
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_160151.jpg$

A7)

I1(t) L.T I1(s)

I2(t) L.T I2(s)

Then express in form

[ I1(s)/I2(s)] [::] = [:]

Drawing the ckl at t = 0-

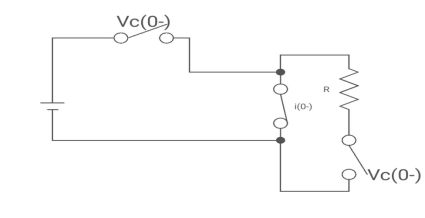
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_160708.jpg$

:. The capacitor is connected for long

Vc1(0-)= V

iL(0-) =0

Vc2(0-)=0

At t= 0+

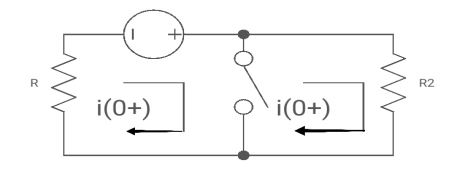
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_161211.jpg$

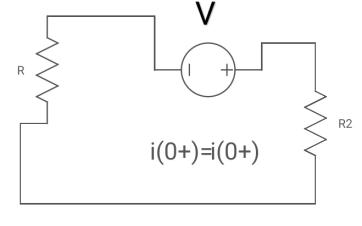
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_161423.jpg$

i1 (0+) = -V/2R

For t>0 the circuit is

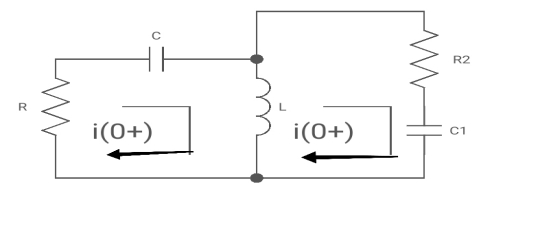
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_161828.jpg$

Apply KVL

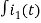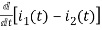-R i1(t) -1/c dt -L=0

Also, we can deduce i1(t)- i2 (t) = iL(t)

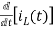-Ri1(t) -1/c - L = 0

-RI1(s)-[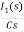-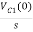]-L[sI1(s)-iL(0-)]=0

- RI1(s)-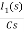 - -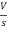s L I2(s)=0

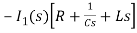- s L I2(s)= - 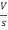(1)

Again

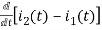-Ri2(t) ) -1/c dt -L=0

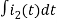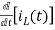-Ri1(t) -1/c - L = 0

Taking Laplace Transform

-RI2(s)- [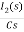 -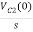]- L[s IL(s)- iL(0-)]=0

-RI2(s)- 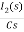-Ls[ I1(s)- I2(s)]=0

- s L I1(s)=0 (2)

Hence in matrix representation

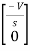
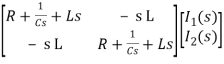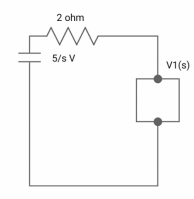
Q8) All initial conditions are zero i(t) L.T, I(s), then find I(s)?

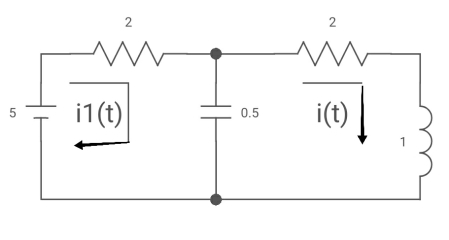
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_162652.jpg$

A8)

Drawing Laplace circuit

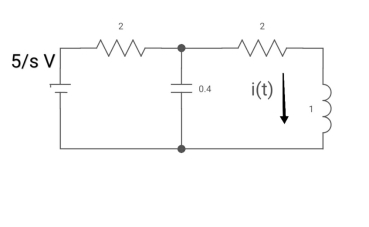
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_162827.jpg$

(2+S) 11 2/S

Zeq = [(2+S)2/S]/[2+S+2/S]=[2(S+2)]/[S2+2s+2]

$C:\Users\TARUNA\Desktop\internship\29 dec 2019\IMG_20191228_132621.jpg$

V1(s) = [5/S{2(S+2)/S2+2S+2}]/[2+{2(S+2)/ S2+2S+2}]

V1(s) = [5(S+2)/S]/[S2+ 3S +4]

I(s) = V1(s)/(S+2) =(5/S)/(S2+35+4)

Q9) The switch is at before moving to position = at t= 0, at t= 0+, i1(t) is

(a) –V/2R (b) –V/R (c) – V/4R (d) 0

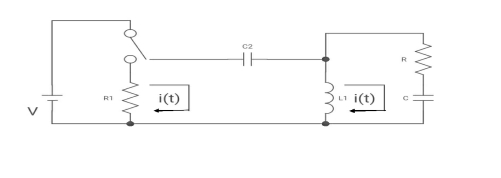
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_160151.jpg$

A9)

I1(t) L.T I1(s)

I2(t) L.T I2(s)

Then express in form

[ I1(s)/I2(s)] [::] .[:]

Drawing the ckt at t = 0-

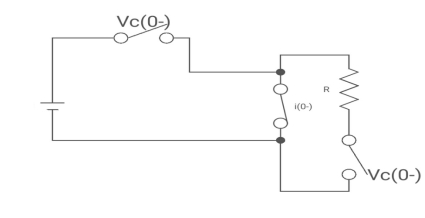
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_160708.jpg$

:. The capacitor is connected for long

Vc1(0-)= V

iL(0-) =0

Vc2(0-)=0

At t= 0+

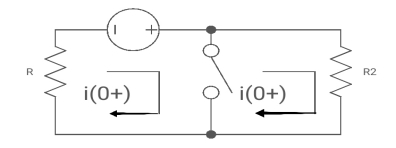
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_161211.jpg$

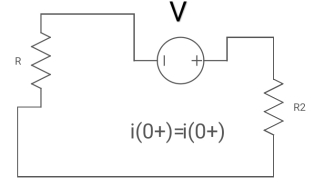
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_161423.jpg$

Fig. Circuit at t=0+

i1 (0+) = -V/2R

For t>0 the circuit is

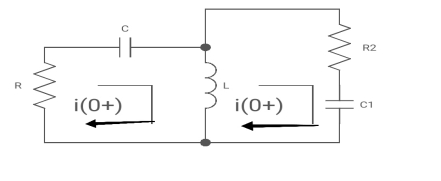
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_161828.jpg$

Fig. KVL in Circuit

Apply KVL

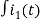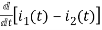-R i1(t) -1/c dt -L=0

Also, we can deduce i1(t)- i2 (t) = iL(t)

-Ri1(t) -1/c 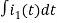- L = 0

-RI1(s)-[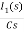-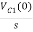]-L[sI1(s)-iL(0-)]=0

- RI1(s)- - -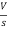s L I2(s)=0

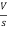- s L I2(s)= - (1)

Again

-Ri2(t) ) -1/c 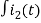dt -L=0

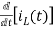-Ri1(t) -1/c - L = 0

Taking Laplace Transform

-RI2(s)- [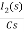 -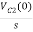]- L[s IL(s)- iL(0-)]=0

-RI2(s)- 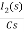-Ls[ I1(s)- I2(s)]=0

- s L I1(s)=0 (2)

Hence in the matrix representation

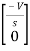
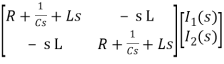Q10) All initial conditions are zero i(t) I(s), then find I(s)?

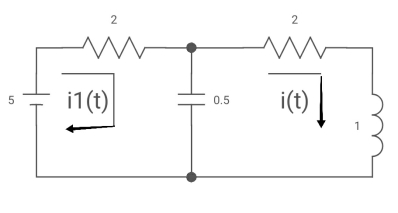
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_162652.jpg$

A10)

Drawing Laplace circuit

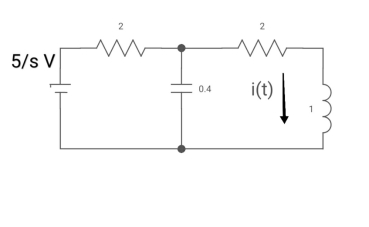
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191231_162827.jpg$

(2+S) 11 2/S

Zeq = [(2+S)2/S]/[2+S+2/S]=[2(S+2)]/[S2+2s+2]

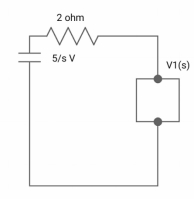
$C:\Users\TARUNA\Desktop\internship\29 dec 2019\IMG_20191228_132621.jpg$

V1(s) = [5/S{2(S+2)/S2+2S+2}]/[2+{2(S+2)/ S2+2S+2}]

V1(s) = [5(S+2)/S]/[S2+ 3S +4]

I(s) = V1(s)/(S+2) =(5/S)/(S2+35+4)

Q11) There is no initial energy stored in this circuit. Find i1(t) and i2(t) for t>0?

A11)

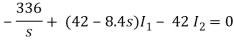
When circuit is closed the network is shown

(10s+90)I2 - 42 I1 = 0

I1 =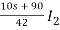

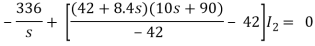
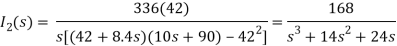
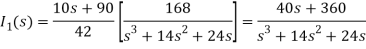
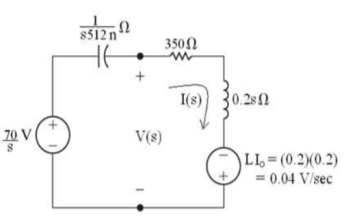
Q12) Find v0 (t) for t > 0.

A12)

Taking Laplace transform of above circuit we have,

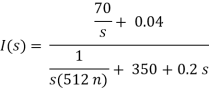
V(s) = (350 + 0.2s)I(s) - 0.04

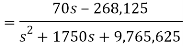
Q13) There is no initial energy stored in this circuit. Find vo if ig = 5u(t) mA.

A13)

Laplace Transform of above circuit we get

By voltage division we get

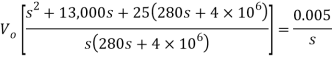
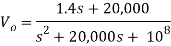
Q14) Find value of current i(t) for the given circuit?

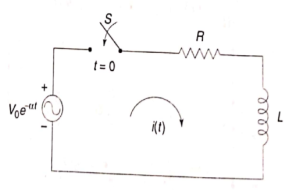
A14)

Applying KVL we get

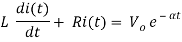
Taking Laplace transform of above equation we get

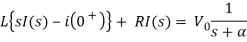
There is no initial current in inductor before closing the switch so i(0+)=0.

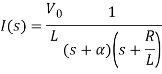
When α ≠

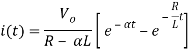
When α =

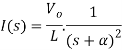
Taking ILT we get

Q15) For the circuit shown below find the value of i1(t) and i2(t) and output voltage across 5 Ohm resistor when the switch is closed also find initial and final values of current?

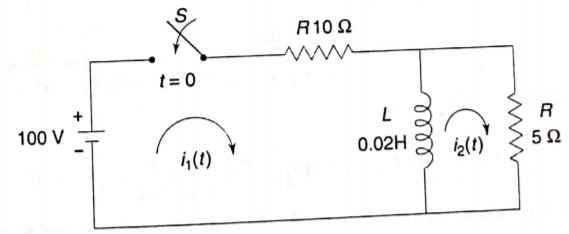
A15)

By KVL we have

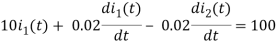
Taking LT of above equations, we get

(10+0.02s)I1(s) - 0.02sI2(s) =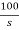

(5+0.02s)I2(s) - 0.02sI1(s) = 0

Solving above equation we get

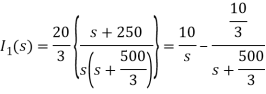
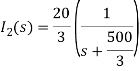
By inverse Laplace transform we get

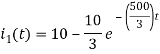
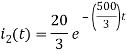
The voltage across 5 Ohm resistor is

The initial value of i1(t) is

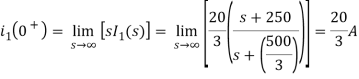
The final value of i2(t) is

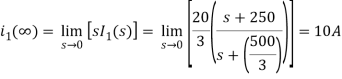
The initial value of i2(t) is

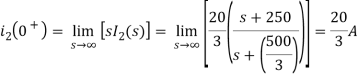
The Final value of i2(t) is

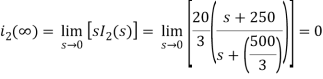
Q16) Find the inverse Laplace transform of

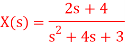
A16)

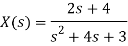
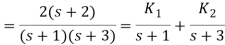
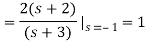
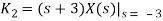
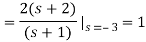
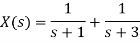
We know that

ℒ{e-αtu(t)} =

Hence,

x(t) = [e-t + e-3t] u(t)

Q17) Find inverse Laplace transform of

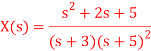
A17)

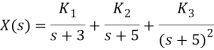
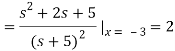
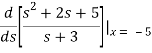
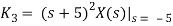
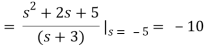
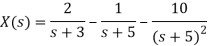
Taking inverse Laplace of above we get

x(t) = 2e-3t -e-5t -10te-5t , t≥0

x(t) = (2e-3t - e-5t - 10te-5t )u(t)

Q18) Find Inverse Laplace transform of

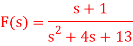
A18)

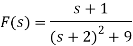
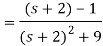
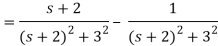
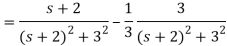
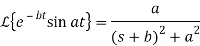
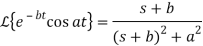
f(t) = ℒ-1 {F(s)}

= e-2t cos 3t - 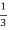e-2t sin 3t

Q19) Find Inverse Laplace Transform of

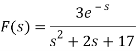
A19)

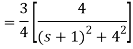
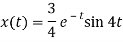
F(s) = e-sX(s)

f(t)= x(t - 1)

Q20) Write equation for initial and final value theorem?

A20)

The initial value theorem

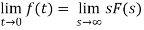
This theorem is valid if and only if f(t) has no impulse functions.

The final value theorem

This theorem is valid if and only if all but one of the poles of F(s) are in the left-half of the complex plane, and the one that is not can only be at the origin.

Sign Up