Unit - 3

Stability & Root Locus method

Q1) Sketch the root locus for given open loop transfer function G(S) =  .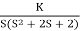

A1)

1) G(s) =

Number of Zeros = 0

Number of polls S = (0, -1+j, -1-j) = (3).

1)     Number of Branches = max (P, Z) = max (3, 0) = 3.

2)     As there are no zeros in the system so, all branches terminate at infinity.

3)     As P>Z, branches terminate at infinity through the path shown by asymptotes

Asymptote = 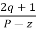× 180°   q = 0, 1, 2………..(p-z-1)

P=3, Z=0.

q= 0, 1, 2.

For q=0

Asymptote = 1/3 × 180° = 60°

For q=1

Asymptote = × 180°

= 180°

For q=2

Asymptote = × 180° = 300°

Asymptotes = 60°,180°,300°.

4)     Asymptote intersects real axis at centroid

Centroid =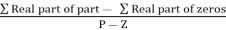

=

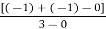
Centroid = -0.66

5)     As poles are complex so angle of departure

øD = (2q+1)×180°+ø

ø = ∠Z –∠P.

Calculating ø for S=0

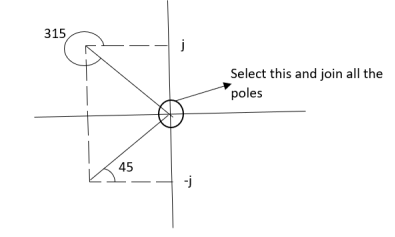
Join all the other poles with S=0

ø = ∠Z –∠P.

= 0-(315°+45°)

= -360°

ØD = (2q + 1)180 + ø.

= 180° - 360°

ØD = -180°     (for q=0)

= 180°           (for q=1)

=540°     (for q=2)

Calculation ØD for pole at (-1+j)

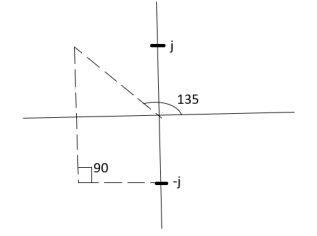
ø = ∠Z –∠P.

= 0 –(135°+90°)

= -225°

ØD = (2q+1) 180°+ø.

= 180-225°

= -45°

ØD = -45°  (for q = 0)

= 315°    (for q = 1)

= 675°   (for q =2)

6)     The crossing point on imaginary axis can be calculated by Routh Hurwitz the characteristic equation is.

1+G(s) H (s) = 0

1+

S (S2+2s+2)+k = 0

S3+2s2+2s+K = 0

For stability 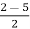  >0. And K > 0.

0<K<2.

So, when K=2 root locus crosses imaginary axis

S3 + 2S2 + 2S + 2 =0

For k

Sn-1 = 0                   n: no. Of intersection

S2-1 = 0                      at imaginary axis

S1 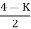= 0

= 0

K<4

For Sn = 0 for valve of S at that K

S2 = 0

2S2 + K = 0

2S2 + 2 = 0

2(S2 +1) = 0

32 = -2

S = ± j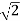

The root locus plot is shown in figure below.

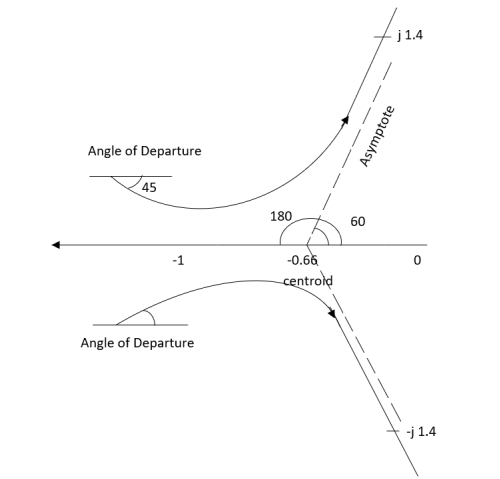
Fig: Root Locus For G(S) =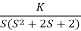 

Q2) Sketch the root locus plot for the following open loop transfer function

G(s) =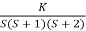

A2)

1. Number of zero = 0, number of poles = 3

2.     As P>Z, branches will terminates at infinity

3.     There are no zeros so all branches will terminate at infinity.

4.     The path for the branches is shown by asymptote

Asymptote = 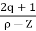×180°. q=0,1,………p-z-1

P=3, Z=0

q= 0,1,2.

For q = 0

Asymptote = × 180° = 60.

For q=1

Asymptote = × 180° = 180°

For q=2

Asymptote = × 180° = 300°

5.     Asymptote intersect real axis at centroid

Centroid =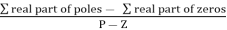

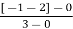= = -1

6.     As root locus lies between poles S= 0, and S= -1

So, calculating breakaway point.

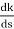= 0

The characteristic equation is

1+ G(s) H (s) = 0.

1+ = 0

K = -(S3+3S2+2s)

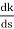= 3S2+6s+2 = 0

3s2+6s+2 = 0

S = -0.423, -1.577.

So, breakaway point is at S=-0.423

Because root locus is between S= 0 and S= -1

7.     The intersection of root locus with imaginary axis is given by Routh criterion.

Characteristics equation is

S3+3S3+2s+K = 0

For k

Sn-1= 0                   n: no. Of intersection with imaginary axis

n=2

S1 = 0

  = 0

K < 6Valve of S at the above valve of K

Sn = 0

S2 = 0

3S2 + K =0

3S2 +6 = 0

S2 + 2 = 0

S = ± 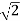j

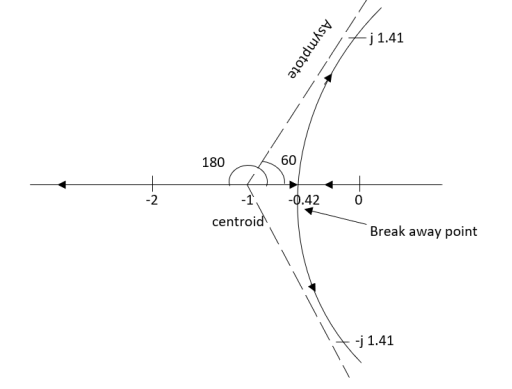
Fig: Root Locus For G(s) =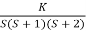

Q3) Plot the root locus for the given open loop transfer function

G(s) =

A3)

1. Number of zeros = 0 number of poles = 4

P = (S=0,-1,-1+j,-1-j) = 4

2.     As P>Z all the branches will terminated at infinity.

3.     As no zeros so all branches terminate at infinity.

4.     The path for branches is shown by asymptote.

Asymptote = 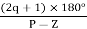       q = 0,1,…..(Þ-z-1)

q=0,1,2,3.             (P-Z = 4-0)

For q=0

Asymptote = ×180° =45°

For q=1

Asymptote = ×180° =135°

For q=2

Asymptote = ×180° =225° 

For q=3

Asymptote = ×180° =315°

5.     Asymptote intersects real axis at unmarried

Centroid =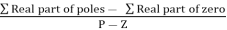

Centroid = 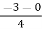= = -0.75

6)     As poles are complex so angle of departure is

ØD = (2q+1) ×180 + ø                       ø = ∠Z –∠P.

a) Calculating Ø for S=0

ø = ∠Z –∠P.

= 0 –[315° + 45°]

Ø = -360°

For q = 0

ØD = (2q+1) 180° + Ø

= 180 - 360°

ØD = -180°

b) Calculating Ø for S=-1+j

ø = ∠Z –∠P.

= 0-[135° + 90° + 90°]

Ø = -315°

For q=0

ØD= (2q+1) 180° +Ø

= 180° -315°

ØD = -135°

ØD for S=1+j        will be ØD = 45°

7)     As the root locus lie between S=0 and S=-1

So, the breakaway point is calculated

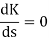
1+ G(s)H(s) = 0

1+ 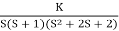= 0

(S2+S)(S2 +2S+2) + K =0

K = -[S4+S3+2s3+2s2+2s2+2s]

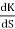= 4S3+9S2+8S+2=0

S = -0.39, -0.93, -0.93.

The breakaway point is at S = -0.39 as root locus exists between S= 0 and S=-1

8)     Intersection of root locus with imaginary axis is given by Routh Hurwitz

I + G(s) H(s) = 0

K+S4+3S3+4S2+2S=0

For system to be stable

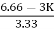>0

6.66>3K

0<K<2.22.

For K = 2.22

3.3352+K =0

3.3352+ 2.22 = 0

S2 = -0.66

S = ± j 0.816.

The root locus plot is shown in figure below.

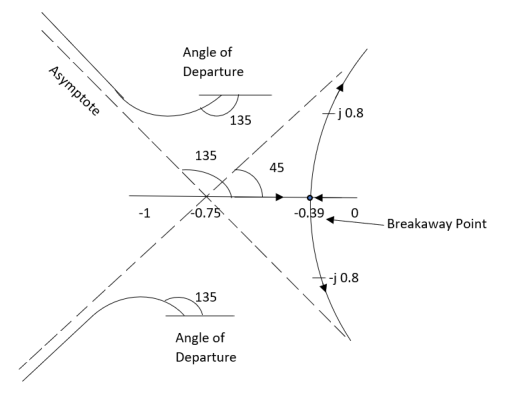
Fig: Root Locus For G(s) =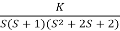

Q4) Plot the root locus for open loop system

G(s) =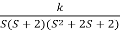

A4)

1)     Number of zero = 0 number of poles = 4 located at S=0, -2, -1+j, -1-j.

2)     As no zeros are present so all branches terminated at infinity.

3)     As P>Z, the path for branches is shown by asymptote

Asymptote =

q = 0,1,2……p-z-1

For q = 0

Asymptote = 45°

q=1

Asymptote = 135°

q=2

Asymptote = 225°

q=3

Asymptote = 315°

4)     Asymptote intersects real axis at centroid.

Centroid =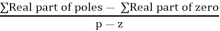

=

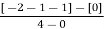
Centroid = -1.

5)     As poles are complex so angle of departure is

ØD=(2q+1)180° + Ø

ø = ∠Z –∠P

= 0-[135°+45°+90°]

= 180°- 270°

ØD = -90°

6)     As root locus lies between two poles so calculating point. The characteristic equation is

1+ G(s)H(s) = 0

1+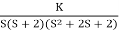= 0.

K = -[S4+2S3+2S2+2S3+4S2+4S]

K = -[S4+4S3+6S2+4S]

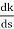= 0

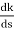= 4s3+12s2+12s+4=0

S = -1

So, breakaway point is at S = -1

7)     Intersection of root locus with imaginary axis is given by Routh Hurwitz.

S4+4S3+6S2+4s+K = 0

≤ 0

K≤5.

For K=5 valve of S will be.

5S2+K = 0

5S2+5 = 0

S2 +1 = 0

S2 = -1

S = ±j.

The root locus is shown in figure below.

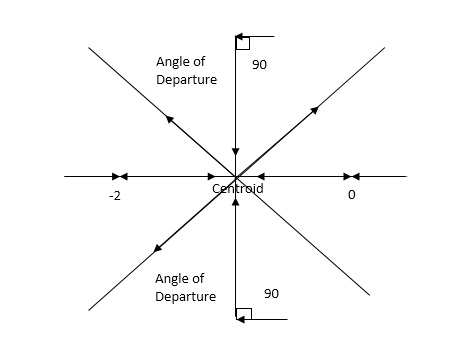
Fig: Root Locus for G(s) =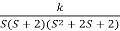

Q5) Plot the root locus for open loop transfer function G(s) =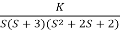

A5)

1. Number of zeros = 0. Number of poles = 4 located at S=0, -3, -1+j, -1-j.

2.     As no. Zero so all branches terminate at infinity.

3.     The asymptote shows the both to the branches terminating at infinity.

Asymptote = 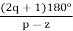q=0,1,….(p-z).

For q = 0

Asymptote = 45

For q = 1

Asymptote = 135

For q = 2

Asymptote = 225

For q = 3

Asymptote = 315

4.     The asymptote intersects real axis at centroid.

Centroid = ∑Real part of poles - ∑Real part of zero / P – Z

= [-3-1-1] – 0 / 4 – 0

Centroid = -1.25

5.     As poles are complex so angle of departure

φD = (29 + 1)180 + φ

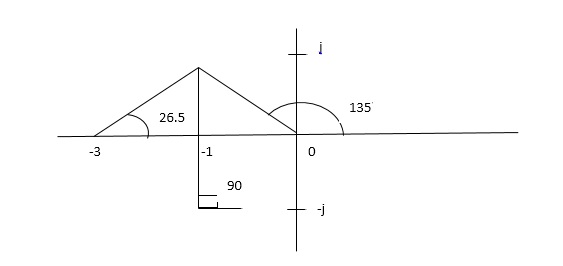
ø = ∠Z –∠P.

= 0 – [ 135 + 26.5 + 90 ]

= -251.56

For q = 0

φD = (29 + 1)180 + φ

= 180 – 215.5

φD = - 71.56

6.     Break away point  dk / ds = 0  is at   S = -2.28.

7.     The intersection of root locus on imaginary axis is given by Routh Hurwitz.

1 + G(S)H(S) = 0

K + S4 + 3S3 + 2S3 + 6S2 + 2S2 + 6S = 0

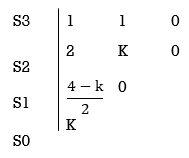
S4 1 8 K

S3 5 6

S2 34/5 K

S1 40.8 – 5K/6.8

K ≤  8.16

For K = 8.16 value of S will be

6.8 S2 + K = 0

6.8 S2 + 8.16 = 0

S2 = - 1.2

S = ± j1.09

The plot is shown in figure below.

Fig: Root Locus for G(s) =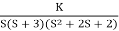

Q6) Sketch the root locus for open loop transfer function.

G(S) = K(S + 6)/S(S + 4)

A6)

1. Number of zeros = 1(S = -6)

Number of poles = 2(S = 0, -4)

2.     As P > Z one branch will terminate at infinity and the other at S = -6.

3.     For Break away and breaking point

1 + G(S)H(S) = 0

1 + K(S + 6)/S(S + 4) = 0

Dk/ds = 0

S2 + 12S + 24 = 0

S = -9.5, -2.5

Breakaway point is at -2.5 and Break in point is at -9.5.

4.     Root locus will be in the form of a circle. So finding the centre and radius. Let S =  + jw.

G( + jw) =  K(  + jw + 6)/(   + jw)(  + jw + 4 ) = +- π 

Tan-1  w/  + 6 - tan-1 w/  – tan-1 w /  + 4 = - π

Taking tan of both sides.

w/  + w/  + 4 / 1 – w/  w/  + 4 = tan π + w /  + 6 / 1 - tan π w/  + 6

w/  + w/  + 4 = w/  + 6[ 1 – w2 /  ( + 4) ]

(2 + 4)(  + 6) = (2 + 4  – w2)

2 2 + 12 + 4 + 24 = 2 + 4 – w2

22 + 12 + 24 = 2 – w2

2 + 12 – w2 + 24 = 0

Adding 36 on both sides

( + 6)2 + (w + 0)2 = 12

The above equation shows circle with radius 3.46 and center(-6, 0) the plot is shown in figure below.

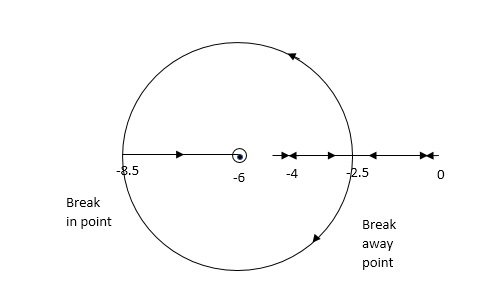
Fig: Root Locus for G(S) = K(S + 6)/S(S + 4)

Q7) What are the effects of adding poles and zeros on a closed to system?

A7) Effect of Addition of Poles:

1)     The root locus is shifted towards imaginary axis.

2)     The system becomes oscillatory.

3)     The stability of system decreases.

4)     The settling time increases.

5)     The range of k reduces.

Effect of addition of zeros

1)     The root locus shifts away from imaginary axis.

2)     Stability of system increases.

3)     The settling time decreases.

4)     The gain margin increases.

5)     The system becomes less oscillatory.

Q8) Explain angle and magnitude criterion for root locus? How can we comment on systems stability from its root locus plot?

A8) Angle condition:

LG(S)H(S) = +-1800(2 KH)        (K = 1,2,3,--)

If angle is odd multiple of 1800 it satisfies above condition.

Magnitude condition:

| G(S)H(S) = 1 | at any point on root locus. The magnitude condition can be applied only if angle condition is satisfied.

Absolutely stable: If the root locus (all the branches) lies within the left side of S-plane it is absolutely stable.

Conditionally Stable:  If some part of the root locus lies on the left half and same

Part on the right of S-plane then it is conditionally stable.

Unstable: If the root locus lies completely on right side of S-plane then it is unstable.

Q9) Determine the stability of the system represent by following characteristic equations using Routh criterion

1)     S4 + 3s3 + 8s2 + 4s +3 = 0

2)     S4 + 9s3 + 4S2 – 36s -32 = 0  

A9)

1) S4+3s3+8s2+4s+3=0

No sign change in first column to no rows on right half of  S-plane system stable.

2) S4 + 9s3 + 4S2 – 36s -32 = 0

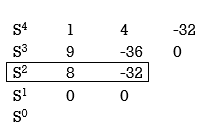
Special case II of Routh Hurwitz criterion forming auxiliary equation

A1 (s) = 8S2 – 32 = 0

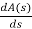= 16S – 0 =0

One sign change so, one root lies on right half S-plane hence system is unstable.

Q10) For using feedback open loop transfer function G(s) =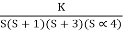

Find range of k for stability

A10)

Find characteristics equation

CE = 1+G (s) H(s) = 0

H(s) =1 using feedback

CE = 1+ G(s)

1+ 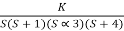= 0

S(S+1)(S+3)(S+4)+k = 0

(S2+5)(S2+7Sα12)αK = 0

S4α7S3α1252+S3α7S2α125αK = 0

S4+8S3α19S2+125+k = 0

By Routh Hurwitz Criterion

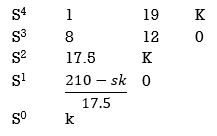
For system to be stable the range of K is 0< K < .

Q11) The characteristic equation for certain feedback control system is given. Find range of K for system to be stable. S4+4S3α12S2+36SαK = 0

A11)

S4+4S3α12S2+36SαK = 0

For stability K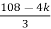>0

> 0

K < 27

Range of K will be 0 < K < 27

Q12) Check if all roots of equation

S3+6S2+25S+38 = 0, have real poll more negative than -1.

A12)

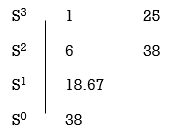
No sign change in first column, hence all roots are in left half of S-plane.

Replacing S = Z-1. In above equation

(Z-1)3+6(Z-1)2+25(Z-1)+38 = 0

Z3+ Z23+16Z+18=0

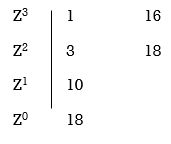
No sign change in first column roots lie on left half of Z-plane hence all roots of original equation in S-domain lie to left half 0f S = -1

Q13) Explain relative stability?

A13) Routh stability criterion deals about absolute stability of any closed loop system. For relative stability we need to shift the S-plane and the apply the Routh criterion.

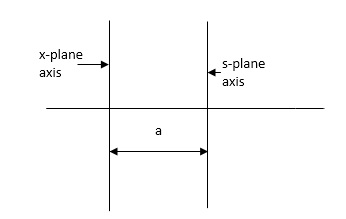
Fig. Location of Pole for relative stability

The above fig 1 shows the characteristic equation is modified by shifting the origin of S-plane to S1= -.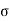

S = Z-S1

After substituting new valve of S =(Z-S1) applying Routh stability criterion, the number of sign changes in first column is the number of roots on right half of S-plane

Q14) What is characteristic equation of a nth order differential equation of LTI discrete system?

A14)

The nth order differential equation of LTI discrete data system can be represented as

y(k+n) +an-1y(k+n-1) +an-2y(k+n-2) +…. +a1y(k+1) +a0y(k)=bmx(k+m) +bm-1x(k+m-1) +…. +b0x(k)

x(k) and y(k) are the inputs and outputs of the system respectively. The z-transform can be obtained as

H(z)=Y(z)/X(z)

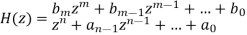                      (i)

The characteristic equation is obtained by equating the denominator to zero

Example: G(s)=2/s(s+2). Find the characteristic equation for the transfer function H(z) with unity feedback. Let T=0.2sec?

Sol:

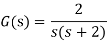
Finding

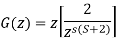
(T=0.2sec)

Hence, the characteristic equation will be

1+G(z)H(z)=0

But there is unity feedback so

1+G(z)=0

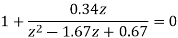
z2-1.34z+0.67=0

The required characteristic equation is z2-1.34z+0.67=0

Q15) How the location of roots of a system effects the time response explain diagrammatically?

A15)

In a system, stability implies small changes in the input do not result in large changes in the output.  A linear time−invariant system is called to be stable, if the output eventually comes back to its equilibrium after disturbances. A linear time invariant system is called as unstable if the output continues to oscillate or increases unbounded from equilibrium state under the influence of disturbance.

For nonlinear system, there may or may not be infinite equilibrium states. Hence to define the concept of stability for such multiple existence equilibrium states is very difficult.

If the impulse response of a system is absolutely integrable, i.e.

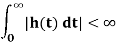
Then the system is said to be stable. The nature of h(t) depends on poles of the transfer function H(s) which are the roots of characteristic equation.

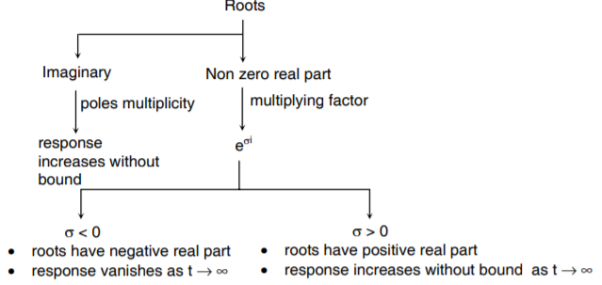
Following conclusions can be drawn:

• If roots have negative real part → impulse response is bounded. System stable.
• If roots have positive real part → system unstable
• If roots are repeated (more than 2) on imaginary axis → system is unstable.
• If roots are non-repeated (one or more) on imaginary axis → system is marginally stable. As h(t) is bounded but ∫h(t) dt is not finite. (oscillatory)

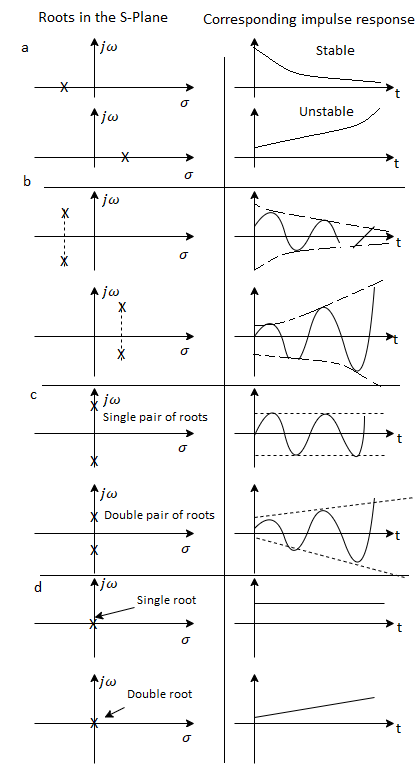
Closed loop poles in the right half s−plane are not permissible as the system becomes unstable.

Q16) For the given polynomials below determine the stability of the system

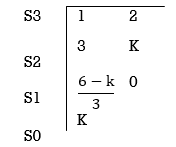
S4+2S3+3S2+4S+5=0

A16)

Arranging Coefficient in Rows.

For row S2first term

S2 = 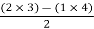= 1

For row S2 Second term

S2 = 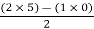= 5

For row S1:

S1 = = -6

For row S0

S0 = 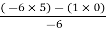= 5

As there are two sign change in the first column, So there are two roots or right half of S-plane making system unstable.