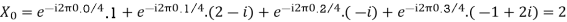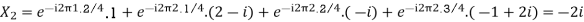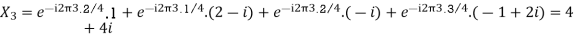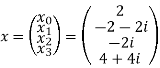Unit - 3
Discrete and Fast Fourier Transforms
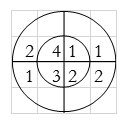
Q1) Find circular convolution using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.
A1)
Circular convolution using circular convolution:
x1x1(n) = {1, 2, 3, 4}
And x2x2 (n) = {1, 2, 1, 2}
L=4, M=4
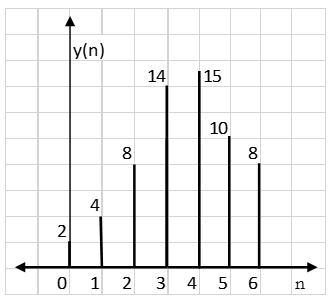
Length of y(n) = L+M-1=4+4-1=7
∴,x1(n) = {1, 2, 3, 4, 0, 0, 0}
& x2(n) = {1, 2, 1, 2, 0, 0, 0}
For y(0),
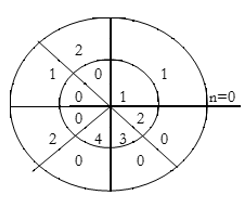
∴ y(0)= 1×1=1
For y(1),
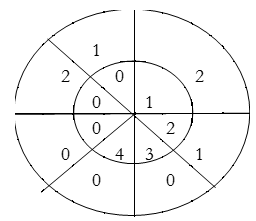
∴ y(1)= 2×1+1×2=4
For y(2),
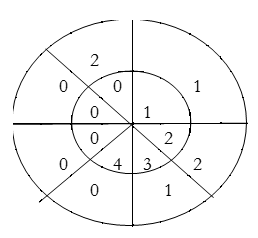
∴ y(2)= 1×1+2×2+3×1=8
For y(3),
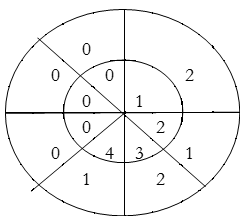
y(3)=1×2+2×1+3×2+4×1=14
For y(4),

∴ y(4)= 4×2+3×1+2×2=15
For y(5),

∴ y(5) = 4×1+3×2=10
For y(6),
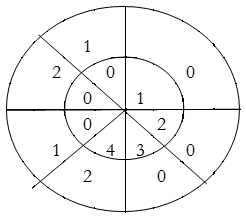
∴ y(6) = 4×2=8
∴y(n) = {1, 4, 8, 14, 15, 10, 8}
Result: y(n) = {2, 4, 8, 14, 15, 10, 8}
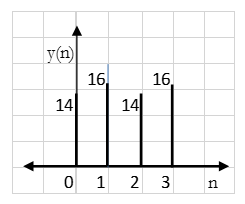
Q2) Find circular convolution using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.
A2) Linear using circular convolution:
For y(0),
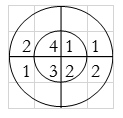
∴ y(0)= 1+4+3+8=16
For y(1),
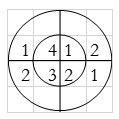
∴ y(1)= 2+2+6+4=14
For y(2),
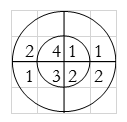
∴ y(2)= 1+4+3+8=16
For y(3),

∴ y(3)= 2+2+6+4=14
y(n) = {16, 14, 16, 14}

Result: y(n) = {14, 16, 14, 16}
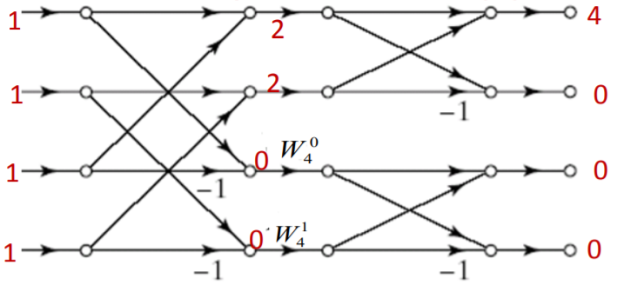
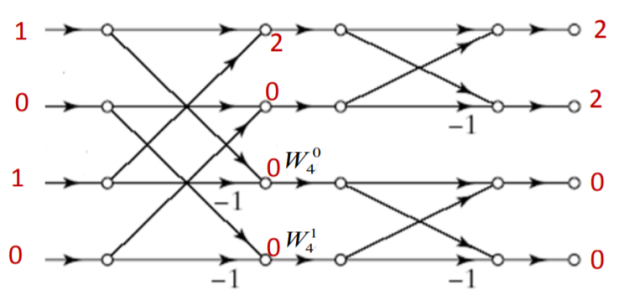
Q3) Find the circular convolution of x(n)={1,1,1,1} and h(n)={1,0,1,0} using DIF-FFT algorithm.
A5) Let us first find 4 point DFTs of x(n) and h(n)
X[K]={4,0,0,0}

H[k]={2,2,0,0}
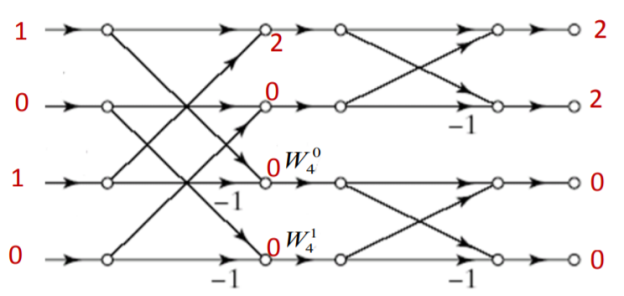
Y[k]= X[k].H[k]
Y[k]={8,0,0,0}
To find y(n)=x(n)⊛h(n), we shall compute IDFT of Y[k]
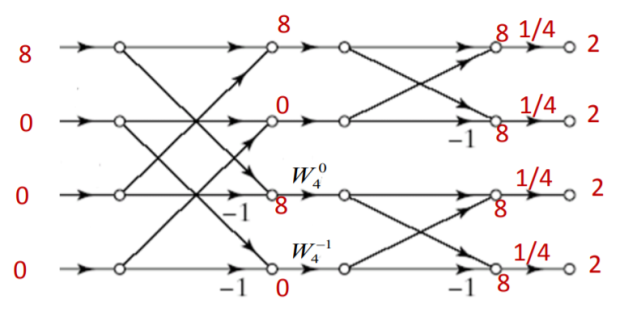
y(n)=x(n)⊛h(n)={2,2,2,2}
Q4) Compute 4-point DFT of given sequence {1,0,0,1}. Use matrix for DFT computation?
A9)
x[n] = {1,0,0,1}
N-1 = 3
N= 4
W4 = 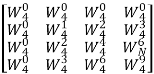 =
= 
X4 = 
X4 = 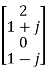
Q5) Compute the N-point DFT of x(n)=3δ(n).
A10)
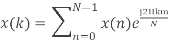
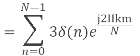

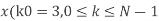
Q6) Compute the N-point DFT of x(n)=7(n−n0)
A11)
We know that,
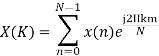
Substituting the value of x(n),
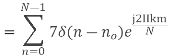
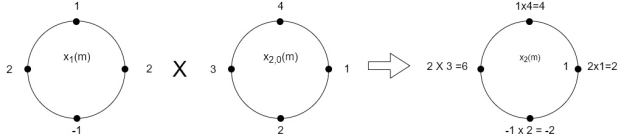
Q7) Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}
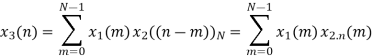
A12)
(2)
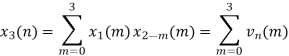
When n=0; 


The sum of samples of v0(m) gives x3(0)
⸫ x3(0)=2+4+6-2=10
When n=1; 
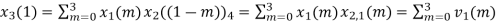
The sum of samples of v1(m) gives x2(1)
⸫ x3(1)=4 + 1 +8-3=10
(3) When n=2; 
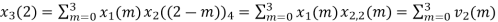
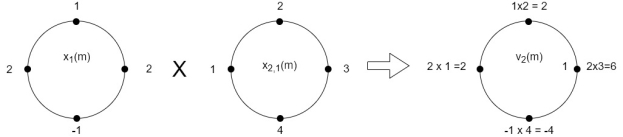
The sum of samples of v2(m) gives x3(2)
⸫ x3(2)=6+2+2-4=6
(4) When n=3; 
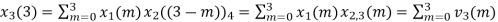
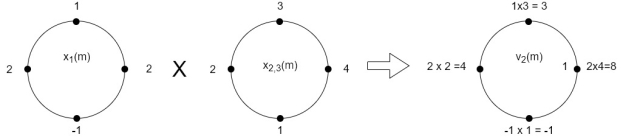
The sum of samples of v3(m) gives x3(3)
⸫ x3(3)=8+ 3+ 4-1= 14
x3(n)={10,10,6,14}
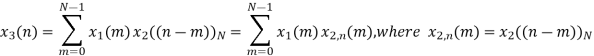

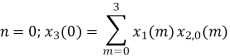
= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)
= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10
Q8) The unit sample response sequence of a system h[n] = {3,2,1}. Use the overlap save method to determine its output sequence in response to the repeating input sequence {2,0,-2,0,2,1,0,-2,-1,0}. Take N=8.
A13)
- h[n] = {3,2,1}, M=3, M-1 =2
- x[n] = {2,0,-2,0,2,1,0,-2,-1,0}
- If N = L+M-1= L+3-1
8=L+2
L=6
The length of block selected is 6.
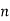 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
 |
|
| 2 | 0 | -2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | … |
 |
| 0) | 2 | 0 | -2 | 0 | 2 | 1 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
| 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 |
|
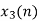 |
|
|
|
|
|
|
|
|
|
|
|
| 2 | 0 | … |
 Block 1
Block 1  Zeros added
Zeros added
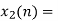 Block 2
Block 2
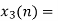 Block 3
Block 3
- Pad L-1 zeros to h[n]. Therefore, sequence will be
h[n] = {3,2,1,0,0,0,0,0}
- Perform circular convolution of h[n] with x1[n] which is shown below
| Periodic extension of data block 1 | Data block 1 | ||||||||||||||
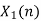 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | |
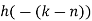 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 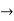 |
|
|
|
|
|
| |
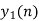 |
|
|
|
|
|
|
| 4 | 1 | 6 | 4 | -4 | 4 | 4 | 7 | |
- Take block 2 and circular convolve with h[n] as shown below
| Periodic extension of data block 2 | Data block 2 | ||||||||||||||
 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | |
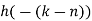 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |  |
|
|
|
|
|
| |
 |
|
|
|
|
|
|
| 8 | 7 | 4 | -5 | -7 | 4 | 5 | 4 | |
- Add y1[n], y2[n] and so on but discard first two values from the answer and save last six values of each circular convolution as shown in figure below.
 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
 | 4 | 1 | 6 | 4 | -4 | -4 | 4 | 7 |
|
|
|
|
|
|
|
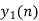 |
|
|
|
|
|
| 8 | 7 | 4 | -5 | -7 | -4 | 5 | 4 |
|
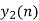 |
|
|
|
|
|
|
|
|
|
|
|
| X | X | … |
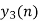 |
|
| 6 | 4 | -4 | -4 | 4 | 7 | 4 | -5 | -7 | -4 | 5 | 4 | … |
Final answer from overlap save method
Q9) The unit sample sequence of a system is h[n] = {3,2,1}. Use overlap add method to determine its output sequence in response to the repeating input sequence {2,0,-2,0,2,1,0,0,-2,-1,0}. Take N=8.
A14)
- h[n] = {3,2,1}, M=3, M-1 =2
- x[n] = {2,0,-2,0,2,1,0,-2,-1,0}
- If N = L+M-1= L+3-1
8=L+2
L=6
From input every time 6 elements are selected and two zeros (M-1) are padded after them as shown below.
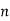 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | … |
|
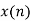 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | -2 | 0 | … |  |
 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 |
|
|
|
|
|
|
|  |
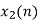 |
|
|
|
|
|
| 0 | -2 | -1 | 0 | 2 | 0 | 0 | 0 |
|  |
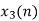 |
|
|
|
|
|
|
|
|
|
|
|
| -2 | 0 | … | 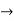 |
Breaking up long input sequence into blocks of data
- Pad L-1 zeros to h[n] sequence. Therefore, sequence will be
h[n] = {3,2,1,0,0,0,0,0}
- Perform circular convolution of h[n] with x1[n] which is shown below
| Periodic extension of data block 1 | Data block 1 |
| ||||||||||||||||
 | 0 | -2 | 0 | 2 | 1 | 0 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 |  | |||
 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |  |
|
|
|
|
|
|  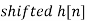 | |||
 |
|
|
|
|
|
|
| 6 | 4 | -4 | -4 | 4 | 7 | 4 | 1 |  | |||
- Now circular convolution is performed for h[n] and x2[n] as shown below.
| Periodic extension of data block 2 | Data block 2 | ||||||||||||||
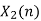 | -2 | -1 | 0 | 2 | 0 | 0 | 0 | 0 | -2 | -1 | 0 | 2 | 0 | 0 | 0 | |
 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 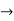 |
|
|
|
|
|
| |
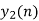 |
|
|
|
|
|
|
| 0 | -6 | -7 | -4 | 5 | 4 | 2 | 0 | |
- Do circular convolution of h[n] with different data blocks. After performing this for all we need to add up all the outputs y1[n], y2[n] and so on.
- While considering all the output sequences we do not discard any values and just keep on adding up the overlapped area as shown below.
 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
 | 6 | 4 | -4 | -4 | 4 | 7 | 4 | 1 |
|
|
|
|
|
|
|
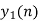 |
|
|
|
|
|
| 0 | -6 | -7 | -4 | 5 | 4 | 2 | 0 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
| X | X | … |
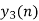 | 6 | 4 | -4 | -4 | 4 | 7 | 4 | -5 | -7 | -4 | 5 | 4 | X | X | … |
Final answer from overlap add method
Q10) Compare DFT and FFT?
A17)
S.NO | Fourier Transform (FT) | Discrete Fourier Transform (DFT) |
1 | FT 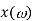 | DFT x(k) is calculated only at discrete values of . Thus DFT is discrete in nature |
2 | The range of is from –π to π or 0 to 2π | Sampling is done at N equally spaced points over version of FT. |
3 | FT is given by equation(1) | DFT is given by equation (2) |
4 | FT equations are applicable to most of infinite sequences. | DFT equations are applicable to casual, finite duration sequences. |
5 | In DSP processors and computers applications of FT are limited because x() is continuous function of . | In DSP processors and computers DFT’s are mostly used APPLICATION a) Spectrum Analysis b) Filter design |
Q11) h(n) = { 1 , 2 , 1, -1 } & x(n) = { 1, 2, 3, 1 } Find y(n).
A18)
Step 1) Find the value of n = nx+ nh = -1 (Starting Index of x(n)+ starting index of h(n))
Step 2) y(n)= { y(-1) , y(0) , y(1), y(2), ….} It goes up to length(xn)+ length(yn) -1. i.e n=-1



Q12) Consider the sequence x[n]={2,1,-1,-3,0,1,2,1}. Calculate the FFT.
A13) Arrange the sequence as x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7)
Since N=8 find the values W8 0 to W 87
Apply the butterfly diagram to obtain the values.
Q13) For N =4 and

Calculate the DFT of x
A20)

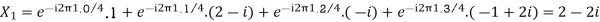

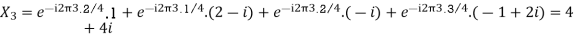
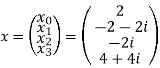
Unit - 3
Discrete and Fast Fourier Transforms
Q1) Find circular convolution using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.
A1)
Circular convolution using circular convolution:
x1x1(n) = {1, 2, 3, 4}
And x2x2 (n) = {1, 2, 1, 2}
L=4, M=4
Length of y(n) = L+M-1=4+4-1=7
∴,x1(n) = {1, 2, 3, 4, 0, 0, 0}
& x2(n) = {1, 2, 1, 2, 0, 0, 0}
For y(0),
∴ y(0)= 1×1=1
For y(1),
∴ y(1)= 2×1+1×2=4
For y(2),
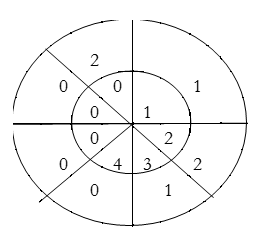
∴ y(2)= 1×1+2×2+3×1=8
For y(3),
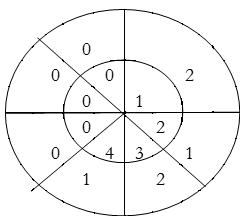
y(3)=1×2+2×1+3×2+4×1=14
For y(4),
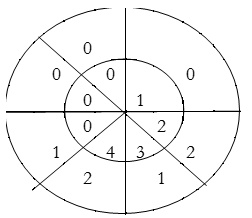
∴ y(4)= 4×2+3×1+2×2=15
For y(5),
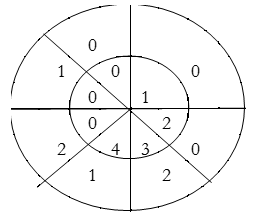
∴ y(5) = 4×1+3×2=10
For y(6),
∴ y(6) = 4×2=8
∴y(n) = {1, 4, 8, 14, 15, 10, 8}
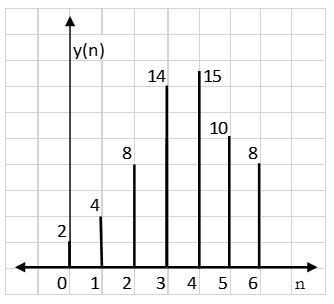
Result: y(n) = {2, 4, 8, 14, 15, 10, 8}
Q2) Find circular convolution using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.
A2) Linear using circular convolution:
For y(0),
∴ y(0)= 1+4+3+8=16
For y(1),
∴ y(1)= 2+2+6+4=14
For y(2),
∴ y(2)= 1+4+3+8=16
For y(3),

∴ y(3)= 2+2+6+4=14
y(n) = {16, 14, 16, 14}
Result: y(n) = {14, 16, 14, 16}
Q3) Find the circular convolution of x(n)={1,1,1,1} and h(n)={1,0,1,0} using DIF-FFT algorithm.
A5) Let us first find 4 point DFTs of x(n) and h(n)
X[K]={4,0,0,0}
H[k]={2,2,0,0}
Y[k]= X[k].H[k]
Y[k]={8,0,0,0}
To find y(n)=x(n)⊛h(n), we shall compute IDFT of Y[k]
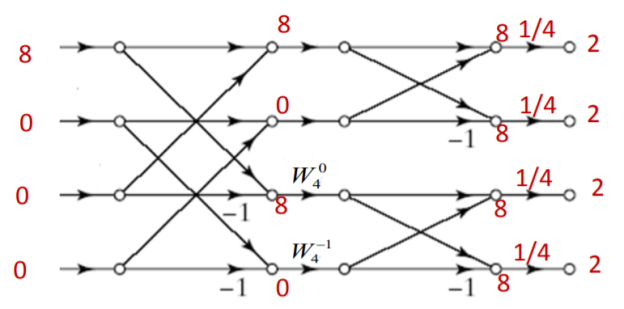
y(n)=x(n)⊛h(n)={2,2,2,2}
Q4) Compute 4-point DFT of given sequence {1,0,0,1}. Use matrix for DFT computation?
A9)
x[n] = {1,0,0,1}
N-1 = 3
N= 4
W4 =  =
= 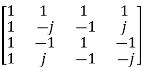
X4 = 
X4 = 
Q5) Compute the N-point DFT of x(n)=3δ(n).
A10)


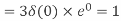

Q6) Compute the N-point DFT of x(n)=7(n−n0)
A11)
We know that,
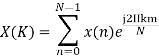
Substituting the value of x(n),
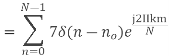
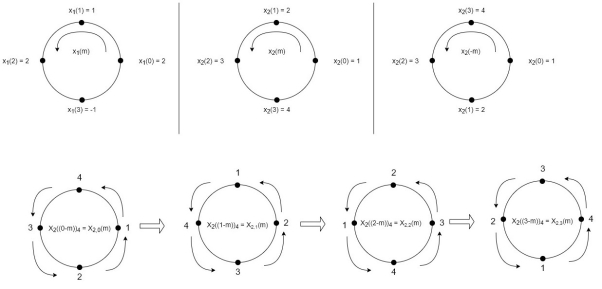
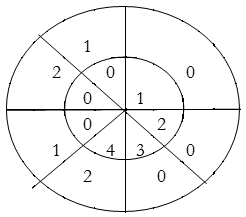
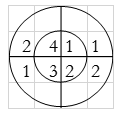
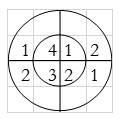
Q7) Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}

A12)

(2)
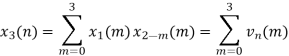
When n=0; 

The sum of samples of v0(m) gives x3(0)
⸫ x3(0)=2+4+6-2=10
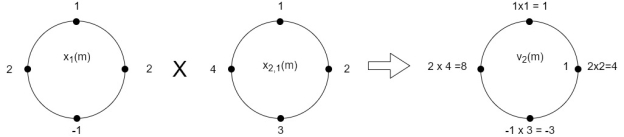
When n=1; 
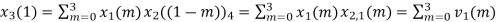

The sum of samples of v1(m) gives x2(1)
⸫ x3(1)=4 + 1 +8-3=10
(3) When n=2; 

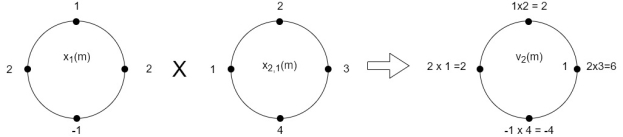
The sum of samples of v2(m) gives x3(2)
⸫ x3(2)=6+2+2-4=6
(4) When n=3; 
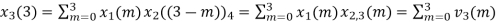
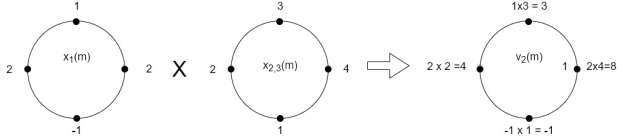
The sum of samples of v3(m) gives x3(3)
⸫ x3(3)=8+ 3+ 4-1= 14
x3(n)={10,10,6,14}
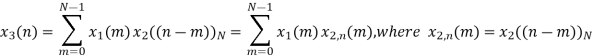
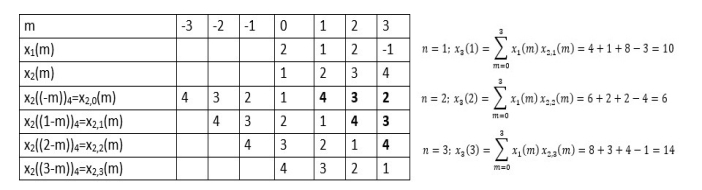
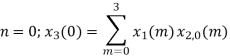
= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)
= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10
Q8) The unit sample response sequence of a system h[n] = {3,2,1}. Use the overlap save method to determine its output sequence in response to the repeating input sequence {2,0,-2,0,2,1,0,-2,-1,0}. Take N=8.
A13)
- h[n] = {3,2,1}, M=3, M-1 =2
- x[n] = {2,0,-2,0,2,1,0,-2,-1,0}
- If N = L+M-1= L+3-1
8=L+2
L=6
The length of block selected is 6.
 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
 |
|
| 2 | 0 | -2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | … |
 |
| 0) | 2 | 0 | -2 | 0 | 2 | 1 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
| 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 |
|
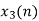 |
|
|
|
|
|
|
|
|
|
|
|
| 2 | 0 | … |
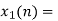 Block 1
Block 1  Zeros added
Zeros added
 Block 2
Block 2
 Block 3
Block 3
- Pad L-1 zeros to h[n]. Therefore, sequence will be
h[n] = {3,2,1,0,0,0,0,0}
- Perform circular convolution of h[n] with x1[n] which is shown below
| Periodic extension of data block 1 | Data block 1 | ||||||||||||||
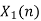 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | |
 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |  |
|
|
|
|
|
| |
 |
|
|
|
|
|
|
| 4 | 1 | 6 | 4 | -4 | 4 | 4 | 7 | |
- Take block 2 and circular convolve with h[n] as shown below
| Periodic extension of data block 2 | Data block 2 | ||||||||||||||
 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | |
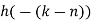 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |  |
|
|
|
|
|
| |
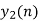 |
|
|
|
|
|
|
| 8 | 7 | 4 | -5 | -7 | 4 | 5 | 4 | |
- Add y1[n], y2[n] and so on but discard first two values from the answer and save last six values of each circular convolution as shown in figure below.
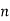 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
 | 4 | 1 | 6 | 4 | -4 | -4 | 4 | 7 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
| 8 | 7 | 4 | -5 | -7 | -4 | 5 | 4 |
|
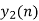 |
|
|
|
|
|
|
|
|
|
|
|
| X | X | … |
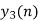 |
|
| 6 | 4 | -4 | -4 | 4 | 7 | 4 | -5 | -7 | -4 | 5 | 4 | … |
Final answer from overlap save method
Q9) The unit sample sequence of a system is h[n] = {3,2,1}. Use overlap add method to determine its output sequence in response to the repeating input sequence {2,0,-2,0,2,1,0,0,-2,-1,0}. Take N=8.
A14)
- h[n] = {3,2,1}, M=3, M-1 =2
- x[n] = {2,0,-2,0,2,1,0,-2,-1,0}
- If N = L+M-1= L+3-1
8=L+2
L=6
From input every time 6 elements are selected and two zeros (M-1) are padded after them as shown below.
 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | … |
|
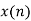 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | -2 | 0 | … |  |
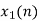 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 |
|
|
|
|
|
|
| 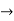 |
 |
|
|
|
|
|
| 0 | -2 | -1 | 0 | 2 | 0 | 0 | 0 |
|  |
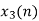 |
|
|
|
|
|
|
|
|
|
|
|
| -2 | 0 | … |  |
Breaking up long input sequence into blocks of data
- Pad L-1 zeros to h[n] sequence. Therefore, sequence will be
h[n] = {3,2,1,0,0,0,0,0}
- Perform circular convolution of h[n] with x1[n] which is shown below
| Periodic extension of data block 1 | Data block 1 |
| ||||||||||||||||
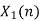 | 0 | -2 | 0 | 2 | 1 | 0 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 |  | |||
 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 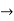 |
|
|
|
|
|
| 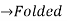 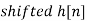 | |||
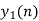 |
|
|
|
|
|
|
| 6 | 4 | -4 | -4 | 4 | 7 | 4 | 1 | 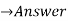 | |||
- Now circular convolution is performed for h[n] and x2[n] as shown below.
| Periodic extension of data block 2 | Data block 2 | ||||||||||||||
 | -2 | -1 | 0 | 2 | 0 | 0 | 0 | 0 | -2 | -1 | 0 | 2 | 0 | 0 | 0 | |
 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |  |
|
|
|
|
|
| |
 |
|
|
|
|
|
|
| 0 | -6 | -7 | -4 | 5 | 4 | 2 | 0 | |
- Do circular convolution of h[n] with different data blocks. After performing this for all we need to add up all the outputs y1[n], y2[n] and so on.
- While considering all the output sequences we do not discard any values and just keep on adding up the overlapped area as shown below.
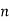 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
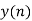 | 6 | 4 | -4 | -4 | 4 | 7 | 4 | 1 |
|
|
|
|
|
|
|
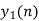 |
|
|
|
|
|
| 0 | -6 | -7 | -4 | 5 | 4 | 2 | 0 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
| X | X | … |
 | 6 | 4 | -4 | -4 | 4 | 7 | 4 | -5 | -7 | -4 | 5 | 4 | X | X | … |
Final answer from overlap add method
Q10) Compare DFT and FFT?
A17)
S.NO | Fourier Transform (FT) | Discrete Fourier Transform (DFT) |
1 | FT  | DFT x(k) is calculated only at discrete values of . Thus DFT is discrete in nature |
2 | The range of is from –π to π or 0 to 2π | Sampling is done at N equally spaced points over version of FT. |
3 | FT is given by equation(1) | DFT is given by equation (2) |
4 | FT equations are applicable to most of infinite sequences. | DFT equations are applicable to casual, finite duration sequences. |
5 | In DSP processors and computers applications of FT are limited because x() is continuous function of . | In DSP processors and computers DFT’s are mostly used APPLICATION a) Spectrum Analysis b) Filter design |
Q11) h(n) = { 1 , 2 , 1, -1 } & x(n) = { 1, 2, 3, 1 } Find y(n).
A18)
Step 1) Find the value of n = nx+ nh = -1 (Starting Index of x(n)+ starting index of h(n))
Step 2) y(n)= { y(-1) , y(0) , y(1), y(2), ….} It goes up to length(xn)+ length(yn) -1. i.e n=-1



Q12) Consider the sequence x[n]={2,1,-1,-3,0,1,2,1}. Calculate the FFT.
A13) Arrange the sequence as x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7)
Since N=8 find the values W8 0 to W 87
Apply the butterfly diagram to obtain the values.
Q13) For N =4 and
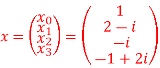
Calculate the DFT of x
A20)