Unit - 1
Fluid Properties
Q1) What are the fluid properties?
A1)
The substance that has a tendency to flow is called as fluid. Generally, fluid is defined as a substance which is capable of spreading and changing its shape, according to is surroundings, without offering internal resistance.
In fluid mechanics, fluid is defined on the basis of its behaviour under the application of external forces. A solid, when subjected to a shearing force, deforms until the internal shear resistance equals the externally applied stress.
Within elastic limits or removal of the external force, the formation disappears and solid comes to its original shape. When a small shearing force is applied externally to the fluid it starts deforming and continues to do as long as applied force exists.
On removal of the external force, the fluid does not come to its original position. On the basis of this property, fluid can be defined as a substance which deforms continuously when subjected to external shearing force. This continuous deformation of fluid is known as flow.
Q2) What are the types of fluid?
A2)
Types of Fluids
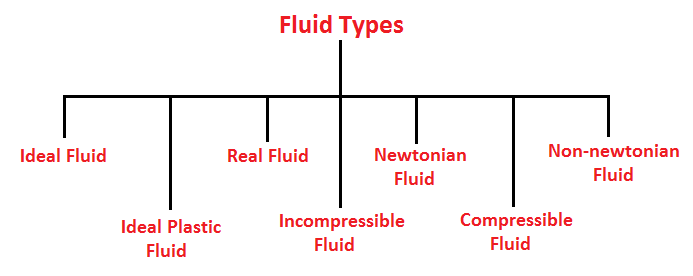
Based on how the property of viscosity of fluid changes in various fluids, they are divided into 5 types.
- Ideal fluid
- Real fluid
- Newtonian fluid
- Non-Newtonian fluid
- Ideal plastic fluid
- Incompressible fluid
- Compressible fluid
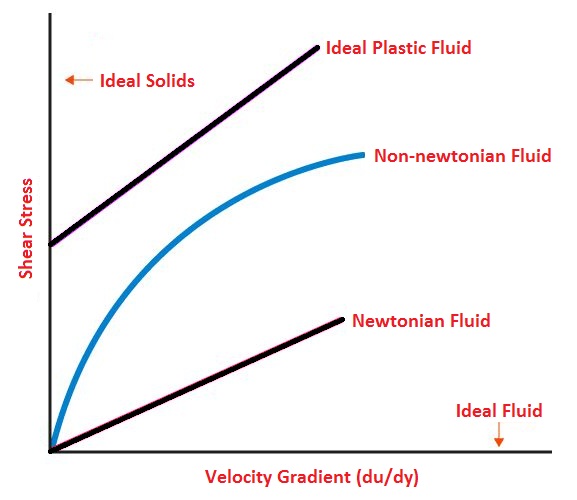
1) Ideal Fluid
The fluid, which is incompressible and has no viscosity or no friction, is known as an ideal fluid. Ideal fluid is only an imaginary fluid.
2) Real Fluid
A fluid, which possesses viscosity or friction, is known as real fluid.
3) Newtonian Fluid
A real fluid, in which the shear stress is directly proportional to the rate of the shear strain, is known as a Newtonian fluid. Fluids obeying Newton’s law where the value of viscosity (μ) is constant are known as Newtonian fluids.
4) Non-Newtonian Fluid
A real fluid, in which the shear stress is not proportional to the rate of the shear strain, is known as a Non-Newtonian fluid. Fluids in which the value of viscosity (μ) is not constant are known as non-Newtonian fluids.
5) Ideal Plastic Fluid
A fluid, in which the shear stress is more than the yield value and shear stress is proportional to the rate of shear strain, is known as ideal plastic fluid.
6) Incompressible Fluid
A fluid, in which the density of the fluid does not change which changes to an external force or pressure, is known as an incompressible fluid.
7) Compressible Fluid
A fluid, in which the density of fluid changes while the change in external pressure or force, is known as compressible fluid.
Q3) Give the graphical representation of fluid.
A3)
Graphical Representation of Fluids
Q4) Give the classification of fluid flows.
A4)
Classifications of Fluid Flows
Some of the general categories of fluid flow problems are as follows;
1. Viscous and in viscid flow:
The fluid flow in which frictional effects become signification, are treated as viscous flow. When two fluid layers move relatively to each other, frictional force develops between them which is quantified by the fluid property ‘viscosity’. Boundary layer flows are the example viscous flow.
Neglecting the viscous terms in the governing equation, the flow can be treated as in viscid flow.
2. Internal and External flow:
The flow of an unbounded fluid over a surface is treated as ‘external flow’ and if the fluid is completely bounded by the surface, then it is called as ‘internal flow’.
For example, flow over a flat plate is considered as external flow and flow through a pipe/duct is internal flow. However, in special cases, if the duct is partially filled and there is free surface, then it is called as open channel flow. Internal flows are dominated by viscosity whereas the viscous effects are limited to boundary layers in the solid surface for external flows.
3. Compressible and Incompressible flow:
The flow is said to be ‘incompressible’ if the density remains nearly constant throughout. When the density variation during a flow is more than 5% then it is treated as ‘compressible’. This corresponds to a flow Mach number of 0.3 at room temperature.
Compressible fluid flow is defined as the flow in which the density is not constant which means the density of the fluid changes from point to point.
The density notation is ρ
ρ ≠ constant
Incompressible fluid flow is defined as the flow in which the density is constant which means the density of the fluid does not change from point to point.
ρ = constant
Gases are compressible fluid flow but whereas the liquid is incompressible fluid flow.
4. Laminar and Turbulent flow:
The highly ordered fluid motion characterized by smooth layers of fluid is called ‘Laminar Flow’, e.g. Flow of highly viscous fluids at low velocities.
The fluid motion that typically occurs at high velocities is characterized by velocity fluctuations are called as ‘turbulent.’ The flow that alternates between being laminar & turbulent is called ‘transitional’.
The dimensionless number i.e. Reynolds number is the key parameter that determines whether the flow is laminar or turbulent.
- If the Reynolds Number is less than 2000, the flow is called Laminar flow.
- Reynolds Number is more than 4000, the flow is called Turbulent flow.
- If the Reynolds Number is lies between 2000-4000, the flow may be laminar or turbulent.
5. Steady and Unsteady flow:
When there is no change in fluid property at point with time, then it implies as steady flow. However, the fluid property at a point can also vary with time which means the flow is unsteady/transient. The term ‘periodic’ refers to the kind of unsteady flows in which the flow oscillates about a steady mean.
 (Steady Flow)
(Steady Flow)
 (Unsteady flow)
(Unsteady flow)
5. Natural and Forced flow:
In a forced flow, the fluid is forced to flow over a surface by external means such as a pump or a fan. In other case (natural flow), density difference is the driving factor of the fluid flow. Here, the buoyancy plays an important role. For example, a warmer fluid rises in a container due to density difference.
6. One/Two/Three dimensional flow: A flow field is best characterized by the velocity distribution, and thus can be treated as one/two/three dimensional flow if velocity varies in the respective directions.
One dimensional flow is that type of flow in which the flow parameter such as velocity is a function of time and one space co-ordinate only, say x.
u=f(x), v=0 and w=0
Where u v and w are velocity component in x,y and z directions respectively.
Two-dimensional fluid flow is the type of flow in which velocity is a function of time and two rectangular space co-ordinate say x,y
u= f1(x,y,), v= f2(x,y,) and w= 0.
Three-dimensional fluid flow is the type of flow in which velocity is a function of time and three mutually perpendicular directions. The function of 3 space coordinates (x,y,z).
u= f1(x,y,z), v= f2(x,y,z) and w= f3(x,y,z).
7. Uniform and non-uniform flow:
This uniform fluid flow is defined as the type of flow in which the velocity at any given time does not change with respect to space (i.e length of direction of the flow).
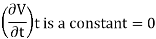
Q5) What is uniform and non uniform flow?
A5)
Uniform flow
Whereas the Non-uniform flow is defined as,
This non-uniform fluid flow is defined as the type of flow in which the velocity at any given time changes with respect to space (i.e. length of the direction of the flow).
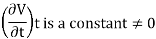
Non-uniform flow
8. Rotational and irrotational Fluid flow:
The rotational fluid flow is defined as the type of fluid flow in which the fluid particles while flowing along streamline and also rotate about their own axis.
Whereas, The Ir-rotational fluid flow is defined as the type of fluid flow in which the fluid particles while flowing along streamline and do not rotate about their own axis.
Q6) Define mass density and specific weight?
A6)
Mass Density
It is defined as the ratio of mass of the fluid to its volume. Its unit is kg/m3 and its dimensional formula is ML-3.
Density depends on temperature and pressure.
Specific Weight
- The specific weight of a fluid is defined as weight per unit volume at a standard temperature and pressure.
- It is denoted by 'w' or ' γ ' (gamma). It has S.I. Unit is N/m3.
- Specific weight of water is 9810 N/m³ (9.81 kN/m³).
- γ =
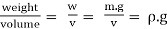
- ∴ γ = ρ.g
- The specific weight depends on gravitational acceleration and the mass density. Since gravitational attraction varies from place to place, the specific weight will also vary.
Q7) Define specific gravity.
A7)
Specific Gravity
- Specific gravity is the ratio of specific weight (or mass density) of fluid to the specific weight (or mass density) of a standard fluid.
- It is denoted by S or RD.
- Specific gravity =
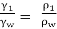
- For liquid, water and for gases, hydrogen or air is consider as a standard fluid.
- Specific gravity of water at a standard temperature 4°C is 1 and that of mercury is 13.6.
Q8) What is newton’s law of viscosity?
A8)
The ratio of shear stress to shear rate is a constant, for a given temperature and pressure, and is defined as the viscosity or coefficient of viscosity.
According to Newton’s law of viscosity the shear stress is directly proportional to rate of shear strain or rate of angular deformation or velocity gradient. The fluid which follows this is law is called Newtonian fluid.
τ α 
τ = μ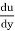
Newton’s law of viscosity is similar to Hooke’s law for solid.
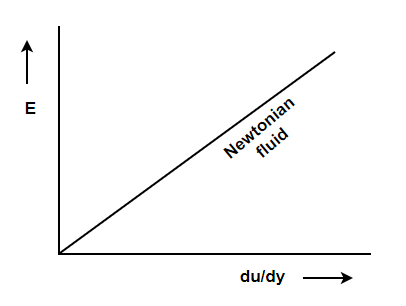
Figure: Diagram for newton’s law of viscosity
Q9) A skater weighing 1000 N attains a speed of 72 km/hour on ice, average skating area being 10 cm². The dynamic coefficient of friction between the Skater and ice may be taken as 0.015. Determine the average thickness of water. Layer existing between the skater and the skating surface. Viscosity of water at 0°C may be taken 1 x 10 N-s/m².
A9)
Given:
W=1000N,
u = 72 kmph = 72x=20m/sec,
A = 10 cm² = 10 x 10 m², -0.015, 10¹N-s/m²
To find: Average thickness.
Force responsible for motion = Frictional resistance
F = μN=pW
Where N= W
F= 0.015 x 1000 = 15 N
Newton's law of viscosity
F = τ.A = 
15 = 1 × 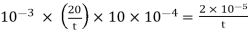
t = 1.33 × 
Average thickness of water layer is 1.33 x 10 m
Q10) A body weighing 1000 N slides down at a uniform speed of 1 m/s along a lubricated Inclined plane making 30° angle with the horizontal. The viscosity of lubricant is 0.1 kg/ms and contact area of the body is 0.25 m². Determine the lubricant thickness assuming linear velocity distribution.
A10)
Given:
W= 1000 N,
θ= 30°
Du = V = 1m/s,
A=0.25 m²
H=0.1 kgm/s 0.1x9.81 Nm/s = 0.981 Nm/s
To find: Lubricant thickness t
Shear force= Weight component along plane
= 1000 sin 30
F = 500 N
Shear stress
τ = 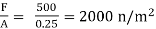
By Newton's law of viscosity
τ = 
τ = 4.905 mm
The lubricant thickness is 4.905 mm.
Q11) What is dynamic viscosity?
A11)
Absolute viscosity - the coefficient of total viscosity - is the measure of internal resistance. Dynamic (absolute) viscosity is the tangential force at each unit area required to move one horizontal plane in relation to another plane - by unit velocity - while maintaining unit distance outside the fluid.
Shave pressure between layers of fluid in straight lines can be defined by Newtonian fluid as
Liquid - viscosity and velocity profile
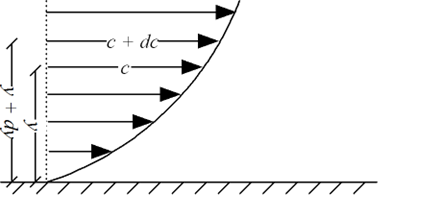
Fig: Dynamic and kinematic viscosity
Shear depression can be shown
τ = μ dc / dy
= μγ. ........ (1)
Where
τ = cutting pressure on liquid (N / m2)
μ = strong viscosity of liquid (N s / m2)
Dc = unit velocity (m / s)
Dy = unit distance between layers (m)
γ = dc / dy = shear rate (s-1)
Equation (1) is known as the Newtons Law of Friction.
(1) Can be rearranged to reflect Dynamic viscosity as
μ = τdy / dc
= τ / γ. .......... . (1b)
- In the SI system the dynamic viscosity units are N s / m2, Pa s or kg / (m s) - where
1 Pa s = 1 N s / m2 = 1 kg / (m s) = 0.67197 lbm / (ft s) = 0.67197 slug / (ft s) = 0.02089 lbf s / ft2
- Strong viscosity can also be expressed in the metric CGS system (centimeter-gram-second) such as g / (cm s), dyne s / cm2 or poise (p) where
1 poise = 1 dyne s / cm2 = 1 g / (cm s) = 1/10 Pa s = 1/10 N s / m2
- Effective use Poise is usually very large and the unit is therefore divided by 100 - into a small centipoise (cP) unit - where
1 P = 100 cP
1 cP = 0.01 poise = 0.01 gram per cm second = 0.001 second Pascal = 1 milliPascal second = 0.001 N s / m2
20.2oC (68.4oF) liquids have a perfect viscosity of one - 1 –centiPoise.
Q12) A plate 0.02 mm distance from a fixed plate, moves at 60 cmvs and requires a force of 3 N/m² to maintain this speed. Determine the fluid viscosity between the plates.
A12)
Given: Distance between plates
Dy= 0.02 mm = 0.02 x 10-3 m
Velocity of upper plate u 60 cm/s 0.6 m/s
Change in velocity du=u-0-0.6 m/s.
τ = Force per unit Area = 3 N/m²
To find: Viscosity
Using Newton's law of viscosity
τ = 
3 = μ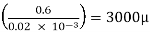
μ = 1×
The fluid viscosity between the plates is 1 x 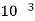 poise,
poise,
Q13) A flat plate of area 2.5 x 10 mm² is pulled with a speed of 0.4m's relative to another plate locate at a distance of 0.15mm from it. Find the force and power required to maintain this speed, if the fluid separating them is having viscosity as 1 poise
A13)
Given:
A=2.5 x 10 mm²=2.5m²,
Du= 0.4m/s dy-0.15mm = 0.15 x 10 m,
μ =1 poise = 0.1N-s/m
To find: Force, power
Using Newton's law of viscosity:
τ = μ
τ = 0.1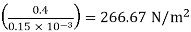
μ = 1 × 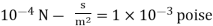
As we known τ = 
F = 266.67 × 2.5 = 666.67 N
Power required to move the plate at speed 0.4 m/s
= Force x Velocity = 666.67 x 0.4 N-m/
1 N-m/s = 1 Watt
P = 266.67 Watt
Power required moving the plate is 266.67 Watt.
Q14) The space between two square flat parallel plates is filled with oil. Each side of the plate is 720 mm. The thickness of the oil film is 15 mm. The upper plate, which moves at 3 ms requires a force of 120 N to maintain the speed. May 2016. 6 Marks
Determine:
(1) The dynamic viscosity of oil.
(2) The kinematic viscosity of oil if the specific gravity of oil is 0.95
A14)
Square plate of side, a = 720 mm=0.72 m
Thickness of oil film, t = 15 mm= 15 x 10
Velocity of plate v= du= 3m/s
Force F= 120 N
Specific gravity s= 0.95
To find μ = v
Mass density,
ρ = s × ρwater
= 0.95 × 1000 = 
Area of plate,
A= 0.72x0.72 = 0. 5184 m²
Using Newton's law viscosity
τ = μ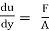
μ × 
Dynamic viscosity μ = 1.157 N/m²
Kinematic viscosity, v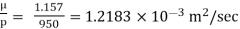
Q15) A body with gravity force of 500 N with a flat surface area 0.2 m slides down a lubricated inclined plane making a 30° angle with the horizontal. For viscosity of 0.1 kg s/m and body speed of 1 m/s. Determine the lubricant film thickness
A15)
Given:
Area A = 0.2 m²
Weight of late W = 500 N
Velocity of plate u = 1 m/sec 0.1kg /m²=0.1 x 9.81 N.s/m² = 0.981 N-s/m²
To find: Thickness of film.
Component of W along the plate W sin 8= 500 sin 30= 250 N
Shear force on the bottom surface of the plate
F = 250N
τ = 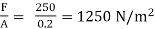
τ = 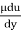
1250 = 0.981 × 
τ = 0.785 × 
The lubricant film thickness is 0.785 mm
Q16) A rectangular plate 1.2 m x 0.4 m. Weighting 970N slides down a 45° inclined surface at a uniform velocity of 2.25 m/s. If the 2mm gap between the plate and the inclined surface is filled with oil, determine the viscosity of oil.
A16)
Given:
Area A = 12x04 0.48 m²
Weight of plate W =970 N
Velocity of plate u = 2.25 m/sec
Thickness of film t = dy = 2 mm = 2 x 10³ m
To find: Viscosity
Component of W along the plate= W sin 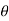
970 sin 45 = 685.97 N
Shear force on the bottom surface of the plate
F= 685.89 N
t = 
1428.94 = μ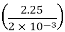
μ = 1.27 N - 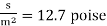
The viscosity of the liquid is 12.7 poise.
Q17) What is strokes theorem?
A17)
Stokes Theorem (additionally called Generalized Stoke’s Theorem) is a assertion approximately the combination of differential bureaucracy on manifolds, which each generalizes and simplifies numerous theorems from vector calculus. As in keeping with this theorem, a line crucial is associated with a floor crucial of vector fields. Learn the stokes regulation right here in element with system and proof.
The Stoke’s theorem states that “the floor vital of the curl of a feature over a floor bounded with the aid of using a closed floor is same to the road vital of the unique vector feature round that floor.”
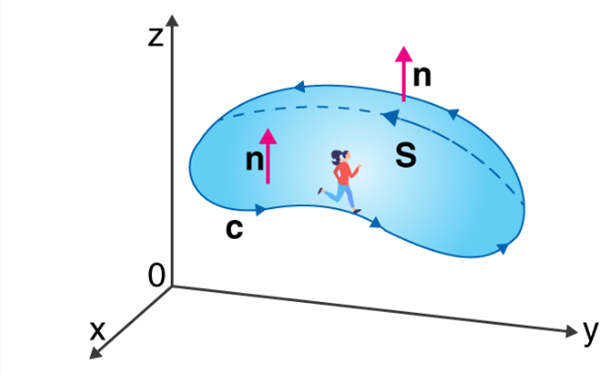

Where,
C = A closed curve.
S = Any surface bounded by C.
F = A vector field whose components have continuous derivatives in an open region of R3 containing S.
This classical declaration, along with the classical divergence theorem, fundamental theorem of calculus, and Green’s theorem are exceptional cases of the general formulation specified above.
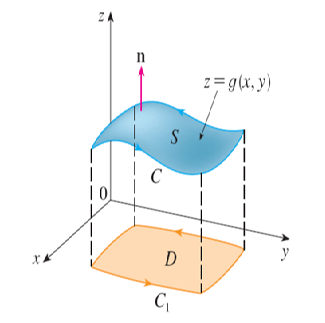
Stokes Theorem Proof:
We count on that the equation of S is Z = g(x, y), (x, y)D
Where g has a non-stop second-order partial derivative.
D is an easy undeniable place whose boundary curve C1 corresponds to C.
Q18) Explain surface tension in detail.
A18)
- The surface tension of a liquid is the property by which a fluid is enables to resist tensile stress.
- It is due to the cohesion between the molecules at the surface of a liquid. It is the force required to maintained unit length of the film in equilibrium. It is denoted by '' (sigma). S.I. Unit = N/m.
- All liquid molecules have tendency to attract each other.
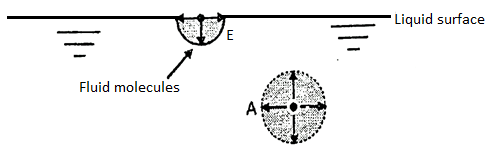
- A liquid molecule on the interior of the liquid body has other molecules on all side of its, so that the forces of attraction are in equilibrium and the molecule is equally attracted on all sides, as a molecule at point A as shown in Fig.
- A liquid molecule at the free surface at point B, does not have liquid molecule above it to pull them outward, so that the free surface molecule tries to move towards the center by downward force.
- This force on the liquid surface is normal to the liquid surface. A film or layer is occurring on the liquid surface which is in tension and resist small loads if placed gently over it.
- It occurs at the interface of a liquid and a gas or at the interface of two liquids and is essentially due to intermolecular forces of cohesion.
- As the temperature increases, the surface tension is decreases.
- A small needle placed gently upon the water surface will not sink but will be supported by the tension at the water surface.
- The effect of surface tension is to reduce the surface of a free body of liquid to a minimum. That is why falling drops of rain become spherical shape.
- Surface tension force can be reduced by the addition of detergents. Surface tension value of liquids when it is cannot with air
σ = 0.073 N/m for air-water interface
σ = 0.480 N/m for air-mercury interface
- Surface tension leads to the phenomena of capillary waves on a liquid surface and capillary rise or depression.
Pressure Intensity Inside a Droplet:
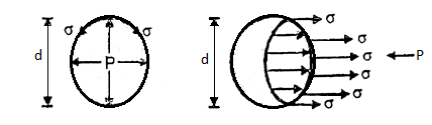
- Consider a spherical droplet of diameter 'd'. Let the excess pressure developed inside the droplet 'P' and ' σ' is the surface tension in the surface of droplet as shown in Fig.
- For static equilibrium condition
- Surface tension force = Force due to excess pressure
- Surface tension x Circumference = Excess pressure x Normal area
σ(πd) = P(
∴ P = 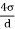
- Thus, pressure intensity inside a droplet varies inversely with the diameter. Pressure intensity decreases with an increase in the size of the droplet.
Q19) Calculate the gauge pressure and the absolute pressure within:
(1) a droplet of water 0.3 cm in diameter
(2) a jet of water 0.3 cm in diameter.
Assume the surface tension of water as 0.07 N/m and atmospheric pressure as 101.3 N/m²
A19)
Given:
d = 3mm = 3 x 10³ m.
σwater = 0.073N/m.
Patm = 101.3 N/m² atm
For droplet and air bubble
P = 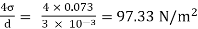
Absolute pressure. (P) = Pgauge + Patm = 97.33 + 101.3 = 198.63 N/m²
For jet
P = 
Absolute pressure in jet
Pabs + Patm = 48.67 + 101.3 = 149.97 N/m2
Q20) Determine the diameter of a droplet of water in mm its t pressure inside is to be greater than that outside by 13 Nm². Take a 7.26 10 Nm.
A20)
Given:
P-130 N/m²
σ = 7.26×10^-2 N/m
For droplet, P
P = 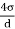
d = 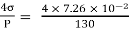 = 2.33 mm
= 2.33 mm
The diameter of a droplet of water is 2.33 mm