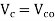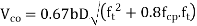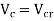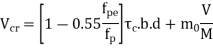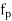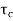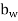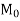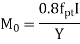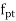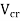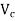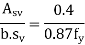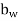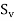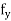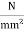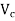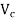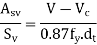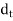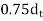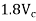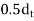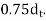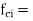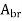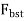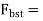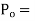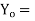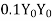undefined | unit 2 prestressed concrete design

SDD3

UNIT 2Question bank Q1) state the assumptions made in determining ultimate flexural strength of PSC members?A1) Design for the limit state of collapse in flexure shall be based on the assumptions given below:-a) Plan sections normal to the axis remain plane after bending.b) The strain in the bonded reinforcement or bonded prestressing Steel weather in tension or in compression is the same as that in the surrounding concrete.c) The maximum strain in concrete at the outermost compression fibre is taken as 0.0035 in the bending.d) The relationship between the compressive stress distribution in concrete and the strain in concrete may be assumed to be rectangular, trapezoid, parabola or any other shape which results in prediction of strength in substantial agreement with the results of tests. An acceptable stress strain curve is given in below figure. DIAGRAM Page no 2 e) For design purposes, the compressive strength of concrete in the structure shall be assumed to be 0.67 times the characteristic strength. The partial safety factor

=1.5 shall be applied in addition to this DIAGRAM Page no 2 Area of stress block=0.36

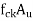Depth of centre of compressive force=0.42

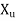a) The tensile strength of the concrete is ignored.b) The stresses in bonded prestressing tendons, weather initially tensioned or un tensioned and in additional reinforcement are derived from the representative stress strain curve for the type of Steel used given by the manufacturer or typical curves given in below figure.

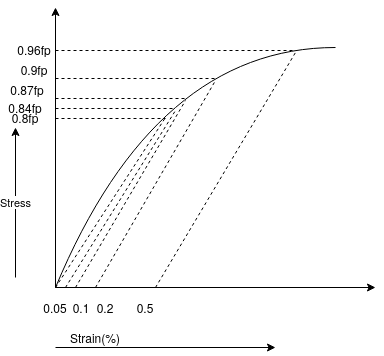
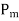For prestressing tendons and in IS-456 for reinforcement. For design purposes, the partial safety factor

equal to 1.15 shall be applied. In addition, the tendon will have an initial prestrain due to prestress after all losses.For members with permanently unbonded internal or externally prestressed tendons, the deformation of the whole member shall be taken into account for calculating strain and stress in the tendon at ultimate condition. In the absence of rigorous analysis, the strain is unbonded tendon shall we assumed not to increase above the initial value due to prestress after all losses. Q2) Draw Stress strain diagram for rectangular section?A2)

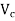Q3) Explain the limit state of collapse in shear, the section uncreacked in flexure?A3)The ultimate share resistance of the concrete alone,

should be considered at both conditions, uncracked and cracked in flexure the lesser value taken and if necessary, shear reinforcement provided.Section uncracked in flexure[ IS 1343-2012, Clause no. 23.4.1, Pp-32]The ultimate share resistance of a section uncracked in flexure,

is given by,

Where,b=breadth of the member which for T,I and L beams should be replaced by breadth of the rib

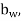D=overall depth of the member

=maximum principal tensile stress given by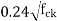

taken as positive where

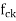is the characteristic compressive strength of concrete.

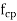=compressive stress at centroidal Axis due to prestress taken as positive in placed members where the centroidal axis occurs in the flange, the principal tensile stress should be limited to

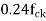at the intersection of the flanged web ; in this calculation, 0.8 times of the stress due to pressure stress at this intersection may be used, in calculating

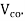4 section and cracked in flexure and with inclined tendons or vertical prestress, the component of prestressing force normal to the longitudinal axis of the member may be added to

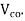Q4) Explain the limit state of collapse in shear, the section ucreacked in flexure?A4)

Section crack in flexure [ IS 1343-2012, Clause no. 23.4.2, Pp-33]

The ultimate shear resistance of a section cracked in flexure, is given by

Where,

=effective prestress after all losses have occurred, which shall not be taken as greater than 0.6

= characteristic strength of prestressing Steel

=Ultimate shear stress capacity of concrete obtained from IS 1342-2012,table 8 PP-33

b=breadth of the member, which, for flanged sections, shall be taken as the breadth of the web

d=distance from the extreme compression fibre to the centroid of the tendons at the section considered

=moment necessary to produce zero stress in the concrete at the depth

=is the stress due to prestress only at a depth of d and distance Y from the centroid of the concrete section which has second moment of area I

V and M= shear force and bending moment respectively, at the section due to ultimate loads.

should be taken as not less than

The value of calculated at a particular section may be assumed constant for a distance equal to d/2, measured in the direction of increasing moment, from that particular section.

For a section cracked in flexure and with inclined tendons, the component of prestressing force normal to the longitudinal axis of the member should be ignored.

Q5) Explain the Shear reinforcement?A5) Shear reinforcement[ IS 1343-2012, Clause no. 23.4.3, Pp-33]

When V, the shear force due to the ultimate loads, is less than , the shear force which can be carried by the concrete, minimum shear A/F should be provided in the form of stirrups such that

Where,

= total cross sectional area of stirrups let's effective in share

b= breadth of the member which for T, I and L beam should be taken at the breadth of the rib

= stirrup spacing long the length of the member, and

= Characteristic strength of the stirrup reinforcement which shall not be taken greater than 415

However, share reinforcement need not be provided in the following cases

a) Where V is less than 0.5

b) In members of minor importance

When V exceeds , share reinforcement shall be provided such that,

In rectangular beams, at both corners in the tensile zone, a stirrup should pass around a longitudinal bar, a tendon or a group of tendons having a diameter not less than the diameter of the stirrup the depth is then taken as the depth from the extreme compression fibre either to the longitudinal bars or to the centroid of the tendons whichever is greater.

The spacing of stirrups along member should not exceed nor 4 times the web thickness for flanged members. When V exceeds the maximum spacing should be reduced to the lateral spacing of the individual legs of the stirrups provided at a cross section should not exceed

Q6) What are the criteria for shear reinforcement as per IS 1343-2012?A6) Maximum shear forces:In no circumstances should the shear force V, due to ultimate loads, exceed the appropriate values given in [ IS 1343-2012]table no.09 PP-34 multipled by bd.

Concrete grade	M-30	M-35	M-40	M-45	M-50	M-55 and over
Maximum shear stress N/mm²	3.5	3.7	4.0	4.3	4.6	4.8

Q7) Explain the Anchorage Zone Stresses?A7)In pretensioned beams, there is a gradual transfer to the prestressing force to the surrounding concrete. As an effect coma a uniform distribution of stresses is present after a certain length from the support section.In post tensioned members, the prestress wires are introduced and then stressed and anchored at the ends. As a result of this, large forces are concentrated over a relatively small areas. This results in the development of transverse and shear stresses. These high stresses develop in concrete at the beam ends.The zone between the end of the beam and the section where only longitudinal stresses exist is called end block or anchorage zone or transfer zone. This zone is of beam length equal to the depth of the beam.The transverse stresses developed in the anchorage zone are tensile in nature over a large length and since concrete is weak in tension. Hence, from the point of view of the designer, it is essential to have a good knowledge of the distribution of stresses in the anchorage zone, so that he/she can provide an adequate amount of steel, properly distributed to sustain the transverse tensile stresses. Permissible bearing stress

IS :1343-2012 Cl No. 19.6.21-a recommends that the permissible stress on concrete, after accounting for all losses due to relaxation of steel, elastic shortening, creep of concrete, sleep in anchorages shall be

Whichever is smaller

Where,

cube strength at transfer

=bearing area

=punching area

- Permissible stress may be increased by 25% at the time of transfer provided the value does not exceed

- The effective punching area shall only be the contact area of the anchorage devices which is circular in shape commercial be replaced by a square of equivalent area the bearing area shall be the maximum area of that portion of the member which is geometric li similar and concentric to the effective punching area.

- In case of embedded anchorages coma bearing stress shall be investigated after accounting for the surface friction between the anchorage and the concrete.

- Where a number of encourages are used, the bearing area shall not overlap, where there is already a compressive stress prevailing over the bearing area comedy total stress shall not exceed the limiting values specified above.

- For stage stressing of the cables, the adjacent unstressed anchorages shall be neglected while determining the bearing area.

Q8) What is Effective punching area and bearing area?A8) Effective punching area and bearing areaThe effective punching area is the area of the anchorage plates/device and the bearing area is the maximum area of that portion of the member which is geometrically is similar and concentric to the effective punching area. Q9) Explain Stress distribution in end block?A9) The forces on the end block of a post tensioned prestressed concrete member are shown in figure below.

A physical concept of the state of stress in the transverse direction, that is normal two planes parallel with the top and bottom surfaces of the beam may be obtained by considering these lines of force as individual fibres acting as curved struts inserted between end force 2P and the main body of the beam.

The curvature of the struts, being convex towards the centerline of the block, induces compressive stresses in zone-A.

In zone B the curvature is reversed in direction and the struts tend to reflect out words, separating from each other and consequently developing transverse tensile stresses.

In zone C, the struts are straight and parallel so that no transverse stresses are induced only longitudinal stresses developed in this zone.

The idealized stress distribution in an end block with the compressive & tensile stress paths is shown in figure below

End blocks of post tensioned beam:- idealized stress paths

The effect of transverse tensile stress is to develop a zone of bursting tension in a direction perpendicular to the anchorage force, resulting in horizontal cracking as shown in figure below

End blocks of post tensioned beams:- bursting tension and spitting cracks

he distribution of transverse stresses in the anchorage zone subjected to a symmetrically placed prestressing force, which is distributed over a small area for

Increasing ratio of

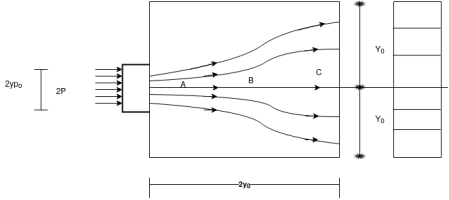
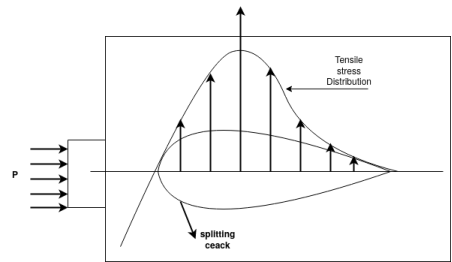
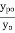varying from zero to 0.5 has been investigated by Guyon.

Q10) Explain Bursting tensile force?A10)

Bursting tensile force[IS 1343-2012, Clause no. 19.6.2.2, pp-26]

a) The bursting tensile forces in the end blocks, or reasons of bonded post tensioned members should be assessed on the basis of the tendon jacking load. For unbonded members, the bursting tensile forces should be assessed on the basis of the tendon jacking load or the load in the tendon at the limit state of collapse, whichever is greater.

The bursting tensile force, existing in an individual square and block loaded by a symmetrically placed square anchorage or bearing plate, may be derived from the equation below:

Where,

bursting tensile force

load in the tendon assessed as above

side of loaded area

side of end block

b)The force will be distributed in a region extending from from the loaded face of the end block. Reinforcement provided to sustain the bursting tensile force may be assumed to be acting at its design strength (0.87 times characteristic strength of R/F) except that the stress should be limited to a value corresponding to strain of 0.01 when the concrete cover to the R/F is less than 50 mm.

c)when circular anchorage or bearing plates are used, the sides of the equivalent square area should be used. Where groups of anchorages or bearing plates occur, the and blocks should be divided into a series of symmetrically loaded prisms and each prism treated in the above manner. For designing and blocks having a c/s of the beam, reference should be made to specialist literature

Q11) What is transmission length?A11)Transmission length:-The prestress is transferred over a certain length from each end of a member, which is called as transmission length.

The stress in tendon is zero at the end of the members. It increases over the transmission length to the effective prestress under services load and remains constant beyond it.

Transmission length needs to be calculated to check the adequacy of prestress in the tendon over the length. A section with high movement should be outside the transmission length, so that tendon retains at least the design effective prestress at the section.

Q12) what are the factors depend upon the transmission length?A12) Transmission length depends upon several factors:-1) Types of tendon such as wire, strand or bar.2) Size of tendon.3) Stress in tendon.4) Surface deformations on the tendon such as:- plain, indented, twisted or deformed tendons.5) Strength of concrete at transfer.6) Pace of cutting tendon like- abrupt flame cutting or slow release of Jack.7) Effect of creep.8) Compaction of concrete.9) Concrete cover.10) Presence of confining reinforcement

Sign Up