Fig.     Fig.

• Active earth pressure is defined as horizontal pressure exerted by retained earth on retaining wall.
• Passive earth pressure is defined as the resisting pressure applied by wall on the retained earth.
• The variation of this earth pressure is linear along the depth of retained earth.
• The total earth pressure up to the depth H (Fig. 3.4) is the area of pressure diagram which is
  1/2 KaWH2 and acts at a height of H/3 from bottom. Hence, moment due to horizontal pressure = KawH3                        ...(1)

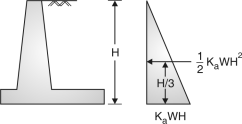
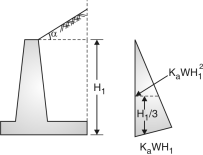
 Where Ka =  and  is the angle of repose of soil.

• In case of a sloping surcharge at an angle  to the horizontal pressure at a depth of H1 due to earth = Ka WH1 and total earth pressure up to a depth of H1 = KaWwhich acts at a height of H1/3 and parallel to the ground surface.

Moment about the base= KaWcos …(2)

 Where, Ka = cos  Fig. 

• If the earth has a level surcharge of ws/unit run, then pressure at all depths is some of magnitude Ka Ws and the surcharge pressure at depth H is Ka Ws H acting at H/2 from bottom (Fig. 3.6)

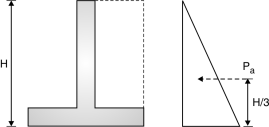
 Moment due to this at bottom =Ka WH2 …(3)

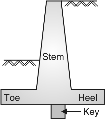
Following guidelines should be adopted while deciding the dimensions of a cantilever retaining wall :

(1) Top width of stem, b2 = 200 mm

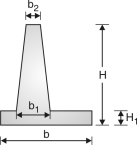
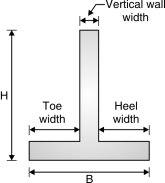
(2) Bottom width – Design for the maximum bending moment.

(3) Height of retaining wall = H

(4) Width of base slab = b

(5) b is usually kept between 0.5 H to 0.6 H for walls without surcharge and 0.7 H for walls with surcharge.

(6) Toe projection = b/3        

Fig.

(7) The thickness of base slab is normally kept as same as the bottom width of stem i.e. b1 = H1

(8) The wall is to be checked for horizontal sliding. The factor of safety against sliding is > 1.5,

 Where W is total vertical load,  is coefficient of friction and p is horizontal earth pressure.

(9) If necessary, a key is provided.

The ratio of overturning moment to the restoring moment should be less than 0.87 or the ratio of restoring moment to the overturning moment should be more than 1.15.

Tentative trial section.  2. Forces

3. Stability check

 (i) Overturning  (ii) Sliding  (iii) Base pressure

4. Design of section

 (i) Vertical wall 

 (ii) Toe slab  

 (iii) Heel slab

 (iv) Counter fort

(I) Trial section :

1. Base width = 0.6 H to 0.7 H (H = total height of wall)

2. Toe width =  to   or 

3. Thickness of vertical walls @ 0.3 m

4. Counter fort thickness @ 0.4 m

5. Thickness of base slab = 2l  or 4l

l  – Spacing of  counter fort in m

H – height in m

Forces:

(1)    Horizontal back fill :

Intensity of earth pressure  = Ka wH

 Ka = Coefficient of active earth pressure.

 Ka  =  

 w  =  unit weight of soil

   = angle of repose Fig. : Pressure distribution diagram (Horizontal backfill)

Total pressure  =  Ka wH H Pa =    KawH2

(2) Inclined backfill (with surcharge) :

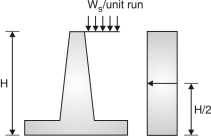
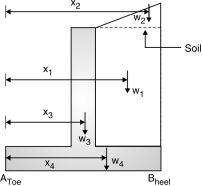
Fig.: Pressure distribution diagram (Inclined backfill)

 Active earth pressure,  Pa   =   Ka w 

  Ka = cos 

 Where, = angle of surcharge  = angle of repose

(3) Passive earth pressure : The passive earth pressure is exerted when it has tendancy to move towards the backfill such a case may occur when the retaining wall supports soil of different depths on boths.

 PP = KpwH2  Kp  =  

(4) Self weight of wall

(i) weight of earth (without surcharge)

 w1 = width  height  density of soil

 x1 = distance of load w1 from toe i.e. (A)

(ii) weight of earth (with surcharge)

 w2  = Area of triangle  density of soil

 x2 = distance of load w2 from A

(iii) weight of wall

 w3 = Thickness  height  density of conc.

 x3 = distance of  load w3 from A  

Fig.:Loads of different parts in retaining wall

(iv) weight of base slab

 w4  = Thickness  width  Density of conc

 x4 = distance  of  load w4 from A

 w = w1 + w2 + w3 + w4   M               @ A

 MToe = w1 x1 + w2 x2  + w3 x3 + w4 x4 

(i) Check against overturning : (Pg 33, cl-20.1)

(1) Overturning moment = Pa

(2) Restoring moment = wx = w1 x1 +w2 x2 + w3x3  ….

 0.9  Restoring moment  1.2  overturning moment

 0.9 wx 1.2  Pa ( safe)

If unsafe change the dimensions

(ii) Check against sliding :  (clause 20.2)

(1) Sliding force  = 1.4  Pa

(2) Restoring force = 0.9  w 

Restoring force  sliding force

0.9  w  1.4  Pa          …Ok

If it is unsafe there is no need to change the dimensions but provide shear key.

(iii) Check for base the pressure :

(1) Maximumpressure = Pmax =

 Eccentricity = e =  – z z = 

 Pmax  S.B.C. of soil

(2) Maximum pressure = Pmin =  0