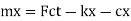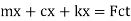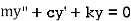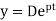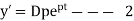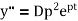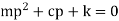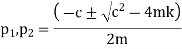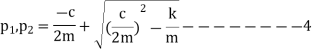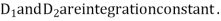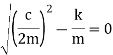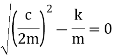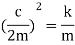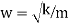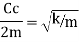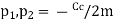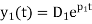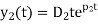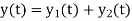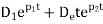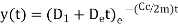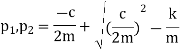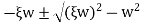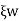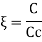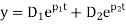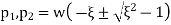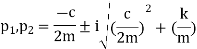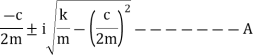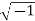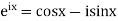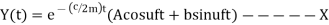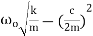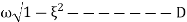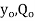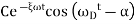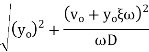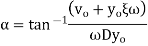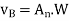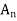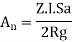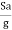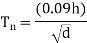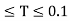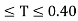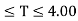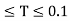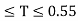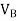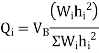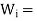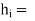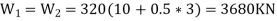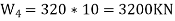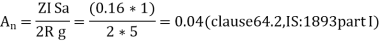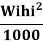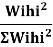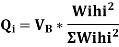|
|
|
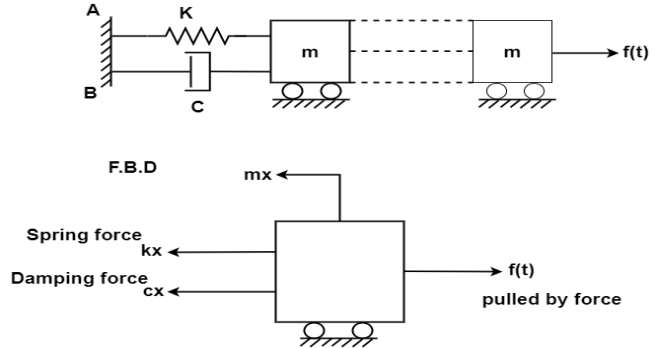
By newton's second law of motion these forces are equal to mx
Distance= velocity* time Velocity/speed= Retardation =-ve sign indicate opposite direction of displacement
|
|
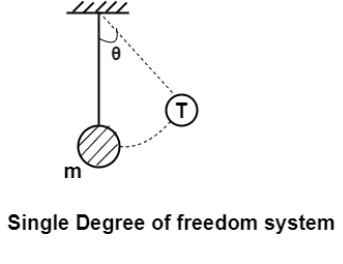
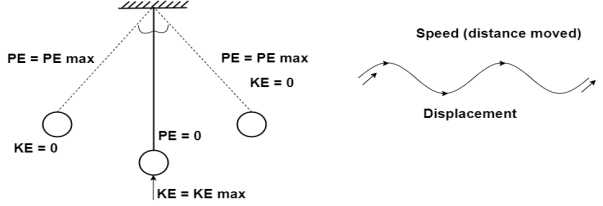
Using D'Alembert’s principle we can write equation of equilibrium to obtain equation of motion. Summation of forces in y direction
Substitute 2 in 1 we get
Thus the general solution of equation 1 is given superposition of the two possible solutions namely.
Where
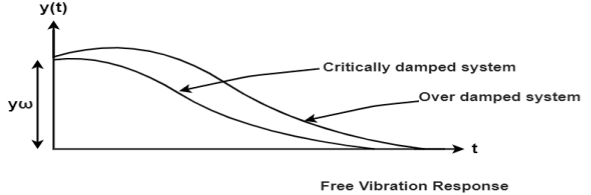
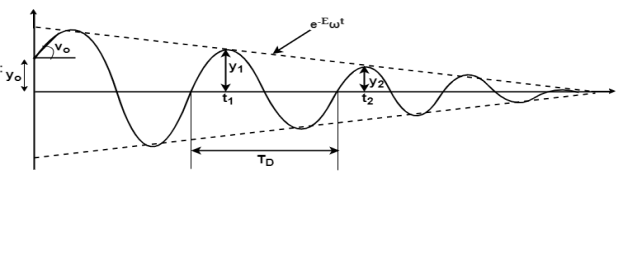
The final solution form of equation V depends on the sign the expression under the radical in equation 4. Three distant cases may occur.
|
The limiting case in which the quantity under radical is zero the damping present in this case is called critical damping.
This means that the expression under root of equation 4 in equal to zero
Cc= 2mw In critically damped system the roots of characteristic equation are equal and from equation 4.
Since the roots are equal the general solution given by equation 5 would provide only one independent constant integration, hence
The general solution for the critically damped system is then given by the superposition of these two solutions
We know that,
|
Expression in the radical of equation 4 thus the solution is ‘
|
In case of underdamped system damping coefficient is less than critical value C<Cc, which occurs when the expression on the radical of equation 4 is negative.
Where i= For this case, we use Euler’s equation which relates exponential and trigonometric functions. Namely,
Substitute A in equation 5 ,we get
Finally when the initial conditions for displacement find velocity
Where
C= max. Amplitude
|
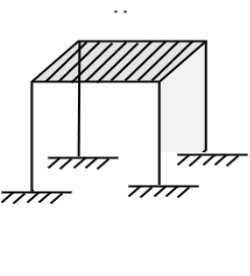
Use of systemic coefficient method As given inIS:-1893 can be carried out to compute forces and moments in the member. This method design base is calculated from
Where,
Where Z=zonal factor given in IS:-1893 , Table 2:- Value Z
I= important factor depending on the functional use of structure (table 6 of IS:-1893) I=1 and 1.50
R=Response reduction factor depending on Pereceivedsiesmic damage performance of structure (Table-7, IS:-1893).
R= 3 to 5 for movement resistant RC structures.
W= seismic waves of the building
The seismic weight of the whole building is the sum of the systemic weights of all the floors and will include 25% and 50% of L.L.for floors in case of LL limit upto3 kN/m and above 3 kN/m and L.L on roof is to be considered.
Sa/g values are obtained on the basic of fundamental/ natural/period of vibration. For moment resistant buildings with brick fell,
Where,h= height of building excluding basement story d=best dimensions of building at plinth level along the considered direction of lateral forces. For moment resistant building without brick fills. Period
Values of Sa/g based on 5% damping
Design base sheer
|
|
From table 6 important factor I=1(all other buildings). Assume the building as special moment resisting frame. Response reduction factor R=5(Table 7, IS:-1893)
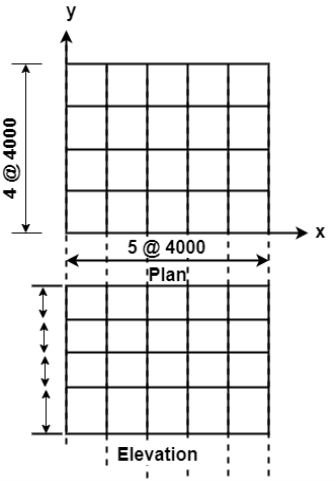
2. Seismic weight:- floor area=20×16=320m Assume DL=10Kn/m Total seismic weight on floors
Roof:-
Total seismic weight of the structure W=ΣWi=3*3680+3200 14240KN 3. Fundamental period:- Lateral load resistance is provided by moment resisting frames infilled with brick marnry panels
From figure 2 of IS: 1893 part I , for T =0.26 sec Sa/g=2.5
4. Design base shear:-
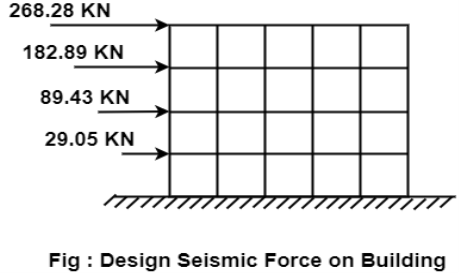
The design base shear is to be distributed with height as per class 7.71 , IS: 1893m part I
|