Unit 1

Linear Differential Equations (LDE) and Applications

Q (1) Solve sin2x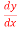= y+tanx

Ans-

Soln :-

The given equation can be written as,

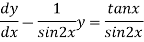
which is a linear diff. eqn.

Now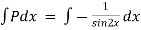

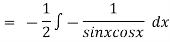
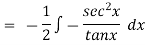
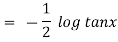
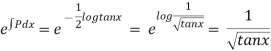
Thus the solution is.

=

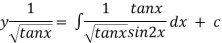
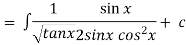
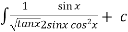
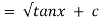
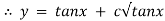
Which is the required solution.

Q(2) Solve  +

Ans-

Soln :-

 This is a linear differential equation

Considr

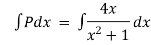
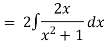
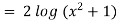
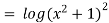
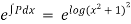
Hence it’s solution is,

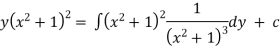
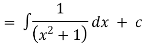
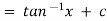
Q(3) Solve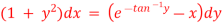

Soln :-

The given eqn can be written as,

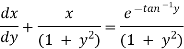
which is a linear diff eqn of the form

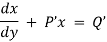
Now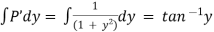

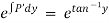
Hence  it’s solution  is

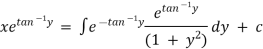
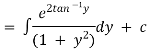
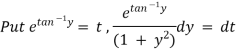
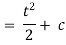
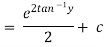
Thus 

Is the required solution of given du=ifferential equation.

Q(4) Solve(1 + x + xy2)dy + (y + y3)dx = 0

Ans-

Soln :-

The given eqn can be written as,

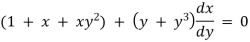
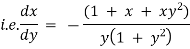
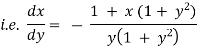
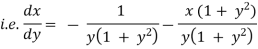
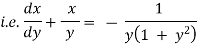
which is of the form,

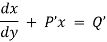
Now,

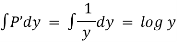
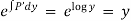
Hence solution is,

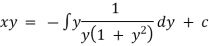
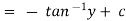
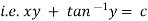
Q(5)  solve

Ans-

Solution:-

     for C.F

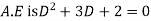
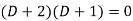
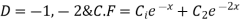
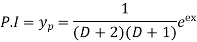
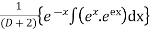      ( put

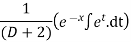
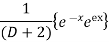
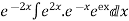
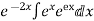
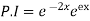
Hence the complete solution is

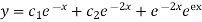
Q(6)   solve

Ans-

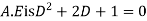
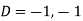
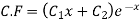
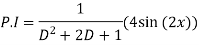
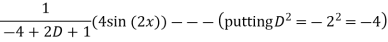
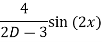
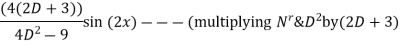
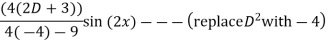
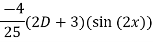
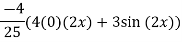
General solution is

Q(7) solve

Ans-

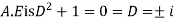
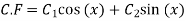
We have ,

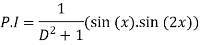
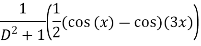
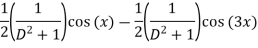
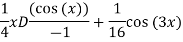
The general solution is

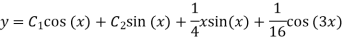
Q(8) solve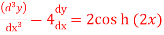

Ans-

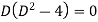
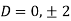
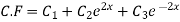
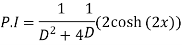
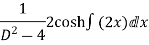
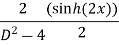
Q(9) Apply method of variation of parameter to solve

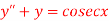
Ans-

Given equation is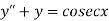   

 Or

  The auxiliary equation is

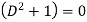
Or

Then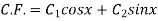

Where 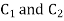are arbitrary constants.

Let P.I =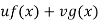

Where

Now ,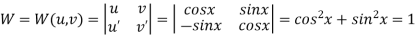

Also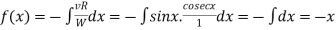

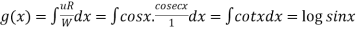
   P.I =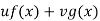

    P.I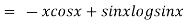 

Hence the general solution is

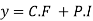
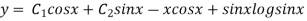
Is the required solution of the given equation.

Q(10) Apply method of variation of parameter to solve

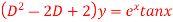
Ans-

Given equation 

  The auxiliary equation is

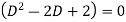
Or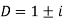

Then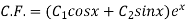

Where 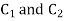are arbitrary constants.

Let P.I =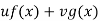

Where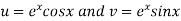

     Now ,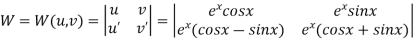

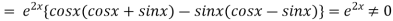
Also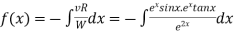

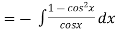
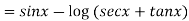
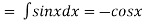
 We have P.I =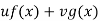

On substitution we get

    P.I. =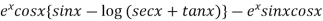 

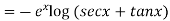
Hence the general solution is

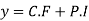
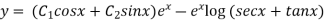
This is the required solution of the given equation.

Q(11) Use the method of variation to solve

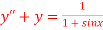
Ans-

Given equation is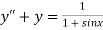 

 Or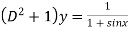

Therefore the auxiliary equation is

Or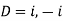

Then C.F.

Where 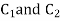are arbitrary constant.

Now, P.I =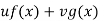

Where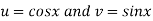

     Now ,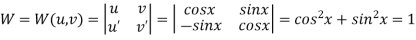

 Also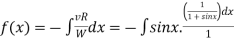

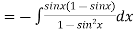
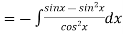
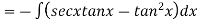
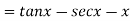
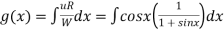
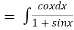
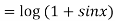
We have P.I =

On substitution we get

    P.I. =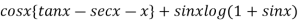 

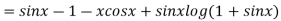
Hence the general solution is

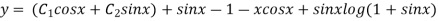
This is the required solution of the given equation.

Q(12) Solve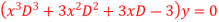

Ans-

Given equation is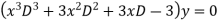 

Let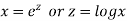

Assume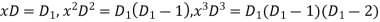

Substituting in above equation we get

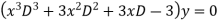
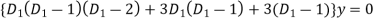
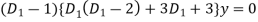
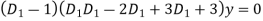
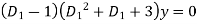
  The auxiliary equation is

Or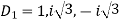

Then solution is

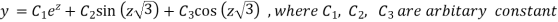
Or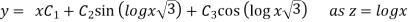

This is the required solution of the given equation.

Q(13) Solve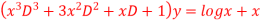

Ans-

Given equation is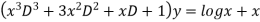 

 Let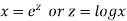

Assume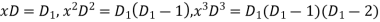

Substituting in above equation we get

  +

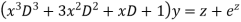
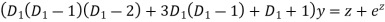
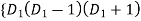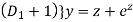
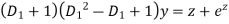
  The auxiliary equation is

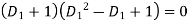
Or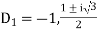

Then C.F.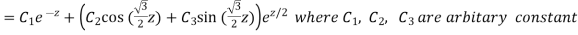

= 

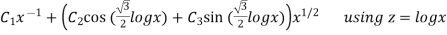
P.I.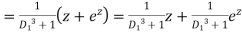

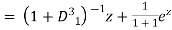
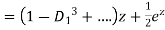
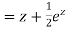
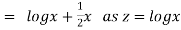
Hence the general solution is

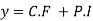
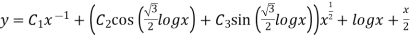
This is the solution of the given equation.

Q(14) Solve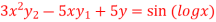

Ans-

Given equation can be re-write as

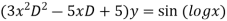
Let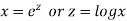

Assume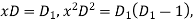

Substituting in above equation we get

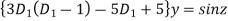
Or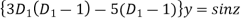

Or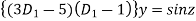 

The auxiliary equation is

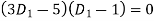
Or

Then C.F.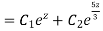  

Or C.F. =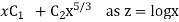

P.I. =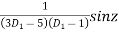 

     (

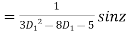
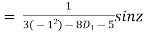
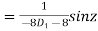
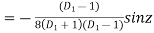
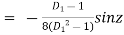
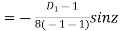
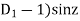
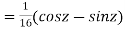
   Hence the general solution is

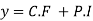
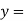
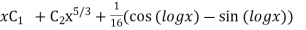
This is the required solution of  the  given equation.

Q(15) Solve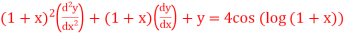

Ans-

Given equation can re-write

  {

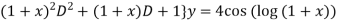
Let

 Assume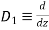

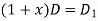
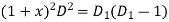
Substituting in above equation we get

{(logz)

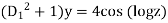
The auxiliary equation is

Or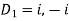

Then C.F.  

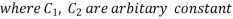
Or C.F.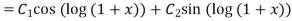

 Now, P.I.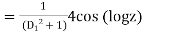

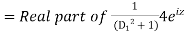
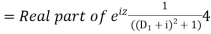
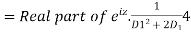
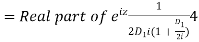
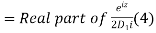
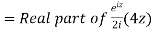
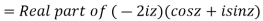
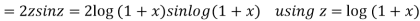
        Hence the general solution is

           +

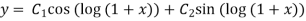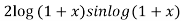
This is the required solution of the given equation.

Q(16): Solve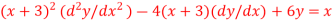 

Ans-

Given equation is

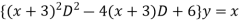
 Let

Assume

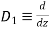
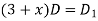
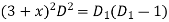
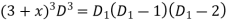
Substituting in above equation we get

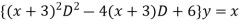
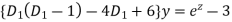
The auxiliary equation is

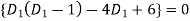
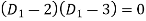
Or 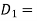2,3

Then C.F.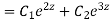  

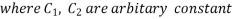
Or C.F.

Now, P.I. =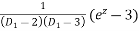

              =

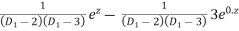
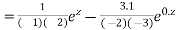
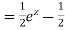
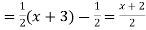
Hence the general solution is

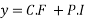
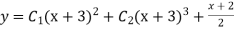
This  is the required solution of the given equation.

Que(17) solve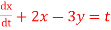

Ans-

Writing in terms of operator 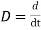  we have

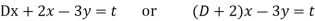----1

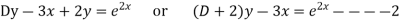
Solving for x (i.e eliminating y  )

Operating 1 by (D+2 ) we have ,

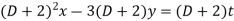
Or 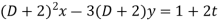---3

Multiplying eq 2 by 3 we get

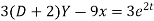
Adding 3 and 4 we get

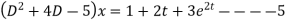
This is a linear differential equation with constant coeff.

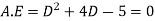
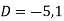
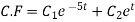
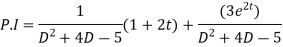
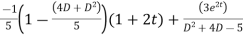
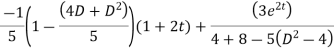
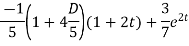
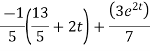
Hence the general solution for x is

Next general solution for (y)

Differentiating equation 6 with respect to t

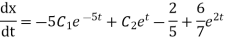
Putting value of x and dx/dt in equation 1  we get

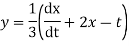
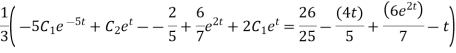
Simplifying we get

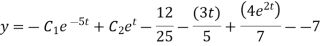
Hence equation 6 and 7 together are the general  solutions

Q(18) solve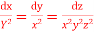

Ans-

Consider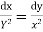

Or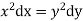

By integrating both sides

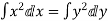
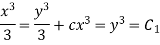
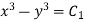—1

Which is the first solution

Now consider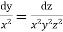

Cancelling the common factor , we have

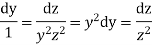
Integrate both sides we get

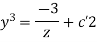
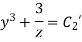
Equation 1 and 2 taken together constitute the answer