Unit 2
Numerical Methods
Q(1) Apply Gauss Elimination method to solve the equations:

Ans-
Given Check Sum (sum of coefficient and constant)
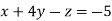 -1 …. (I)
-1 …. (I)
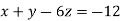 -16 …. (ii)
-16 …. (ii)
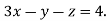 5 …. (iii)
5 …. (iii)
(I)We eliminate x from (ii) and (iii)
Apply eq(ii)-eq(i) and eq(iii)-3eq(i) we get
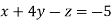 -1 ….(i)
-1 ….(i)
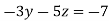 -15 ….(iv)
-15 ….(iv)
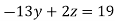 8 ….(v)
8 ….(v)
(II) We eliminate y from eq(v)
Apply 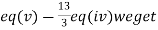
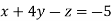 -1 ….(i)
-1 ….(i)
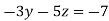 -15 ….(iv)
-15 ….(iv)
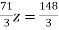 73 ….(vi)
73 ….(vi)
(III) Back Substitution we get
From (vi) we get 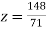
From (iv) we get 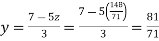
From (i) we get 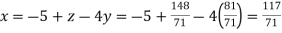
Hence the solution of the given equation is 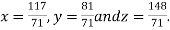
Q(2) Solve the equation by Gauss Elimination Method:
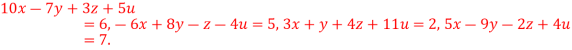
Ans-
Given 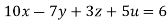
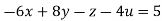
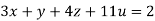
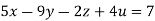
Rewrite the given equation as
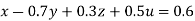 … (i)
… (i)
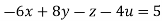 ….(ii)
….(ii)
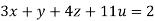 ….(iii)
….(iii)
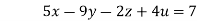 …(iv)
…(iv)
(I) We eliminate x from (ii),(iii) and (iv) we get
Apply eq(ii) + 6eq(i), eq(iii) -3eq(i), eq(iv)-5eq(i) we get
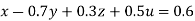 …(i)
…(i)
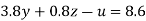 ….(v)
….(v)
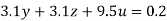 ….(vi)
….(vi)
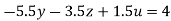 …(vii)
…(vii)
(II) We eliminate y from (vi) and (vii) we get
Apply 3.8 eq(vi)-3.1eq(v) and 3.8eq(vii)+5.5eq(v) we get
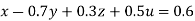 …(i)
…(i)
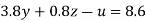 ….(v)
….(v)
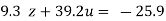 …(viii)
…(viii)
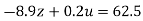 …(ix)
…(ix)
(III) We eliminate z from eq (ix) we get
Apply 9.3eq (ix) + 8.3eq (viii), we get
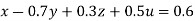 … (i)
… (i)
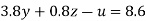 ….(v)
….(v)
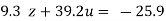 …(viii)
…(viii)
350.74u=350.74
Or u = 1
(IV) Back Substitution
From eq(viii) 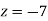
Form eq(v), we get 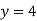
From eq(i) , 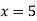
Hence the solution of the given equation is x=5, y=4, z=-7 and u=1.
Que(3) Apply Gauss Elimination Method to solve the following system of equation:
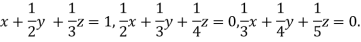
Ans-
Given 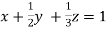 … (i)
… (i)
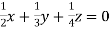 … (ii)
… (ii)
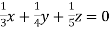 … (iii)
… (iii)
(I) We eliminate x from (ii) and (iii)
Apply 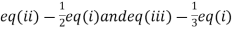 we get
we get
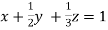 … (i)
… (i)
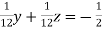 … (iv)
… (iv)
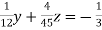 … (v)
… (v)
(II) We eliminate y from (v)
Apply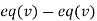 we get
we get
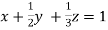 … (i)
… (i)
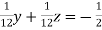 … (vi)
… (vi)
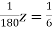 … (vii)
… (vii)
(III) Back substitution
From (vii) 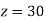
From (vi) 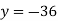
From (i) 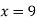
Hence the solution of the equation is 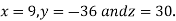
Q(4) Solve by cholesky method
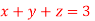
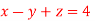

Ans-
Solution. Step I. Consider AX= B
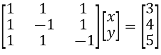
Step 2: Consider 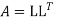
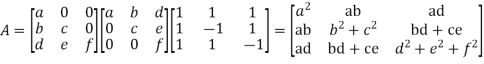
By solving
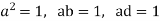
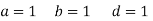
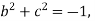
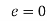 ,
, 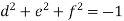
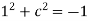
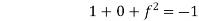
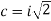

Put all the values
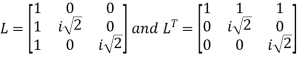
Step 3: LY = B, Let 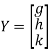
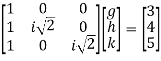
By multiplying and equating
g=3
and, 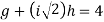
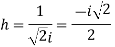
and, 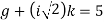
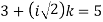
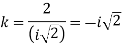
Therefore, 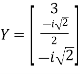
Step 4: 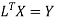
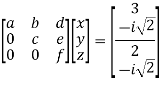
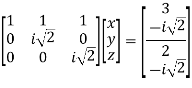
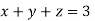
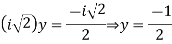
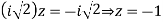
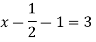
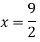
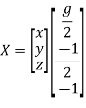
Now we are just cross check our Ans. by putting given equations of question
Given equation: 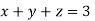
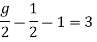
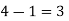
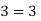
Our answer are correct
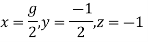
Q(5) Solve by cholesky method
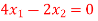
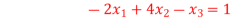
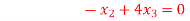
Ans-
Solution.
Step I. consider AX =B
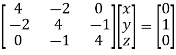
Step 2. Consider 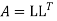
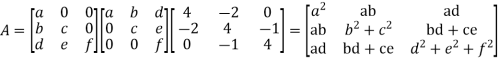
BY solving,
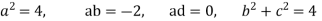
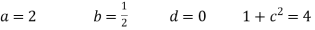

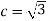



Put all the values we get
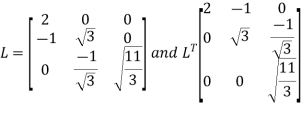
Step 3: LY = B, Let 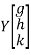
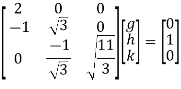
By multiplying and equating
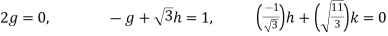

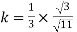
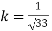
Step 4: 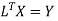
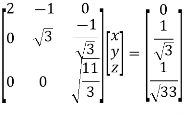
BY MULTIPLYING WE GET
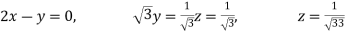
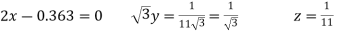
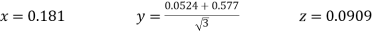
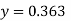
Now we are just cross check our ans by putting values in given equations of question,
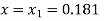
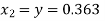
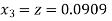
Given equation
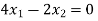
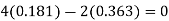
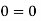
Our answer is correct.
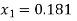
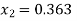
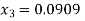
Q(6) Solve by cholesky method
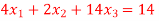
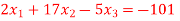
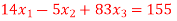
Ans-
Step I Consider AX = B
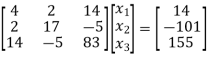
Step 2: Consider 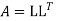
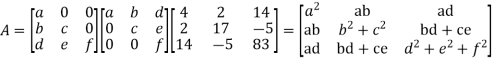
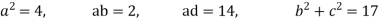
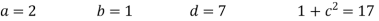


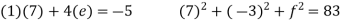



Put all the values we get
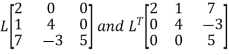
Step 3: 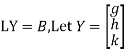
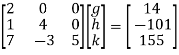
By multiplying and equating
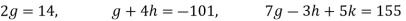

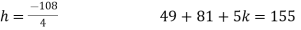
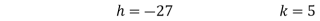
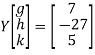
Step 4: 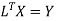
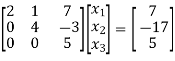
By multiplying we get
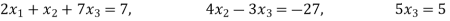
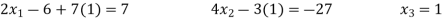



Now we are just cross check our answer by putting values of 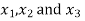 in equation
in equation
Given equation: 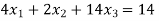
And we have 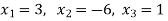
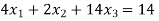
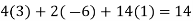
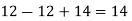
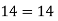
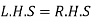
Our correct answer is
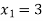
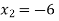
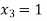
Q(7) Solve by cholesky method
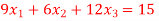
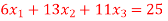
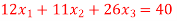
Ans-
Solution-
Step 1. Consider AX = B
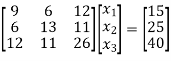
Step 2: Consider, 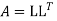
Let, 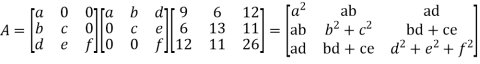
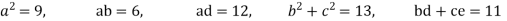



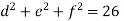
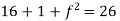
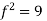
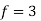
Put all the values we get
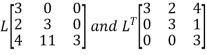
Step 3: LY = B, Let 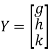
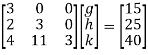
By multiplying and equating
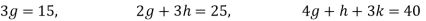
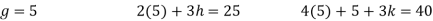


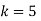
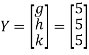
Step 4: 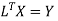
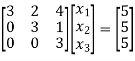
By Multiplying we get
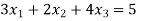
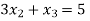
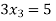
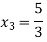
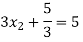
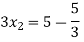
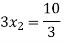
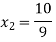
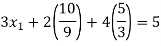
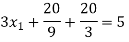
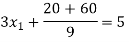
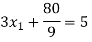
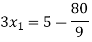
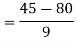
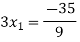
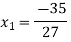
Now we just cross check our answer by putting values in given equation
Given equation: 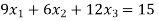
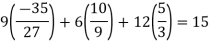
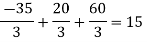
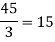
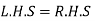
Final answer, 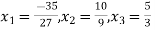
Q(8) Use Jacobi’s method to solve the system of equations:
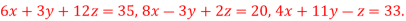
Ans-
Since 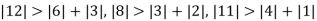
So, we express the unknown with large coefficient in terms of other coefficients.
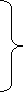
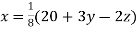
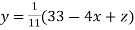 (1)
(1)
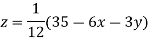
Let the initial approximation be 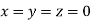
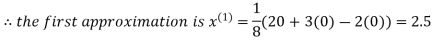
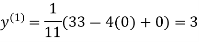
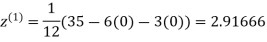
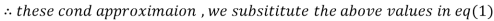
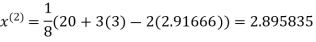
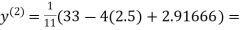 2.35606
2.35606
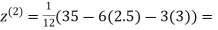 0.91666
0.91666
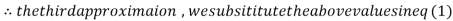
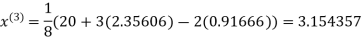
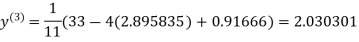
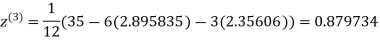
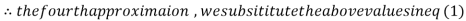
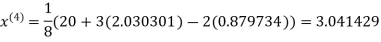
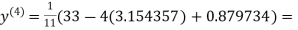 1.932936
1.932936
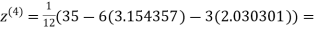 0.831912
0.831912
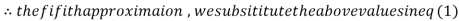
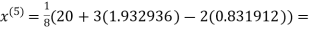 3.016873
3.016873
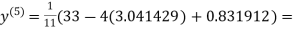 1.969654
1.969654
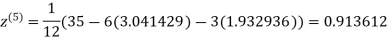
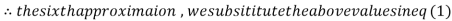
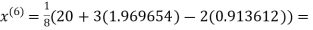 3.010217
3.010217
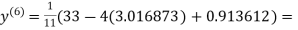 1.986010
1.986010
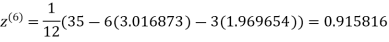
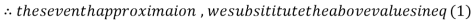
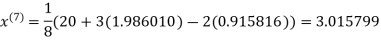
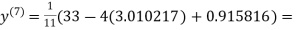 1.988631
1.988631
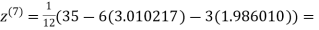 0.915055
0.915055
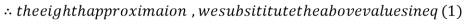
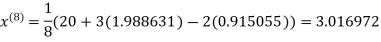
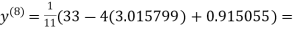 1.986532
1.986532
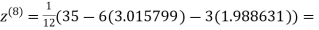 0.911609
0.911609
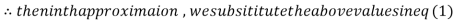
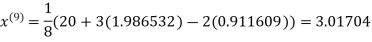
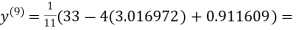 1.985792
1.985792
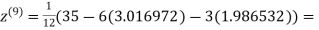 0.911547
0.911547
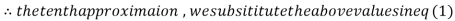
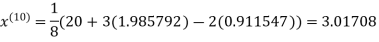
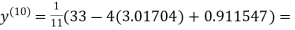 1.98576
1.98576
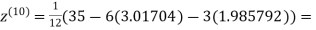 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 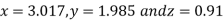
Q(9) Solve by Jacobi’s Method, the equations
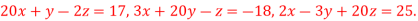
Ans-
Given equation can be rewrite in the form
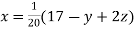 … (i)
… (i)
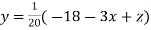 ..(ii)
..(ii)
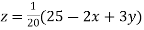 ..(iii)
..(iii)
Let the initial approximation be 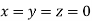
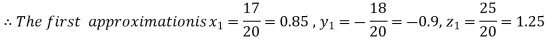
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
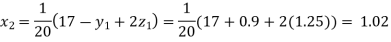
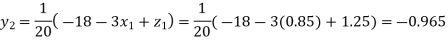
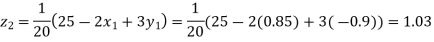
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
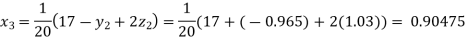
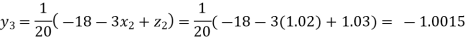
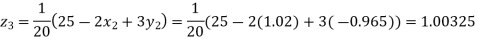
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
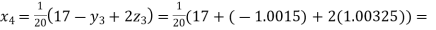 0.90025
0.90025
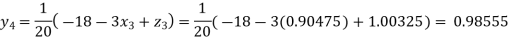
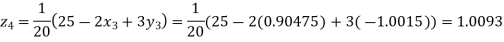
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
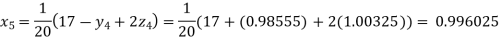
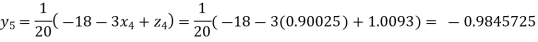
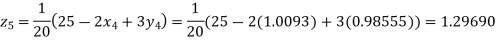
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
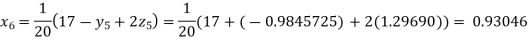
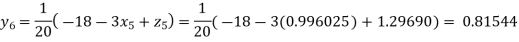
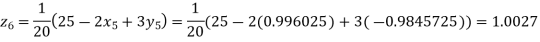
Hence solution approximately is 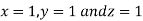
Que(10) Use Jacobi’s method to solve the system of the equations
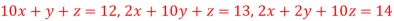
Ans-
Rewrite the given equations
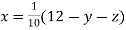
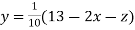 (1)
(1)
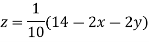
Let the initial approximation be 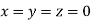
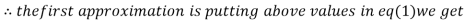
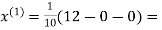 1.2
1.2
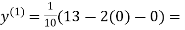 1.3
1.3
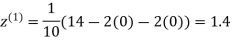
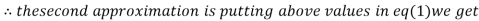
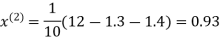
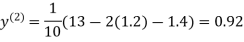
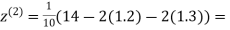 0.9
0.9

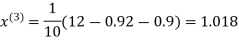
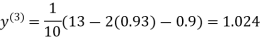
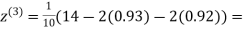 1.03
1.03
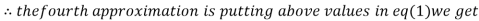
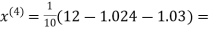 0.9946
0.9946
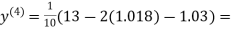 0.9934
0.9934
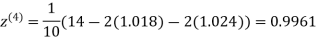

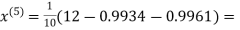 1.0015
1.0015
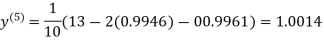
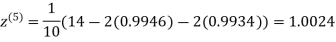
Hence the solution of the above equation correct to two decimal places is
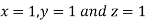
Q(11)Use Gauss –Seidel Iteration method to solve the system of equations

Ans-
Since 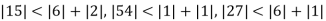
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
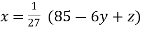
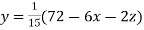 (1)
(1)
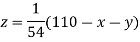
Let the initial approximation be 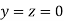
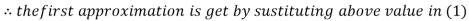
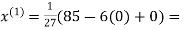 3.14814
3.14814
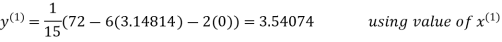
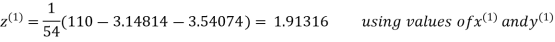
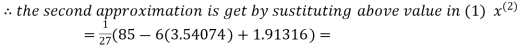 2.43217
2.43217
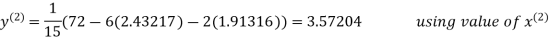
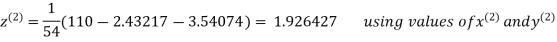
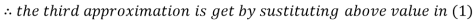
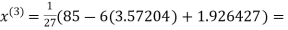 2.42571
2.42571
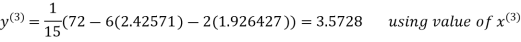
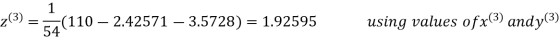
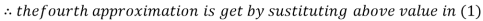
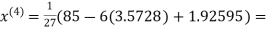 2.4260
2.4260
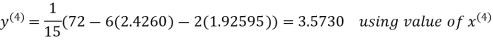
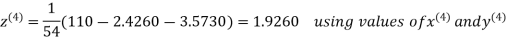
Hence the solution correct to three decimal places is
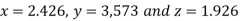
Que(12) Solve the following system of equations
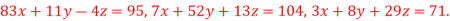 By Gauss-Seidel method.
By Gauss-Seidel method.
Ans-
Rewrite the given system of equations as
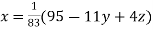
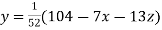 (1)
(1)
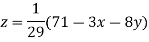
Le t the initial approximation be 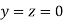
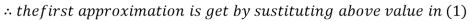
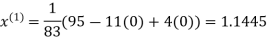
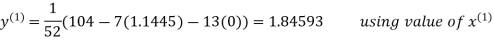
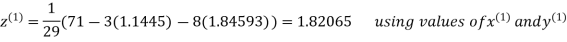
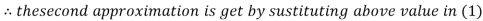
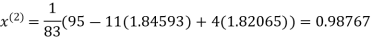
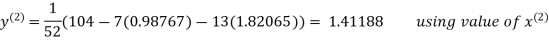
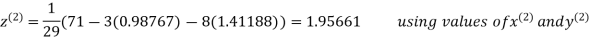
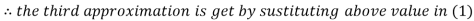
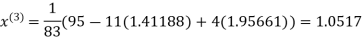
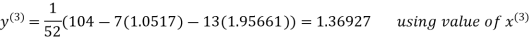
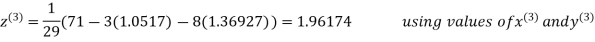
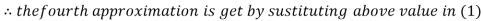
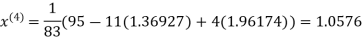
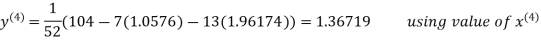
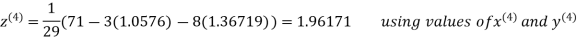
Thus the required solution is 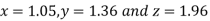
Que(13) Solve the following equations by Gauss-Seidel Method
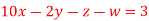
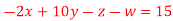

Ans-
Rewrite the above system of equations
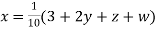
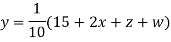
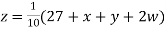 (1)
(1)
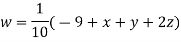
Let the initial approximation be 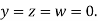

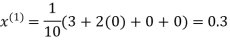
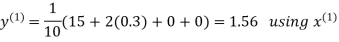
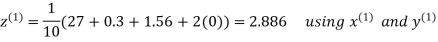
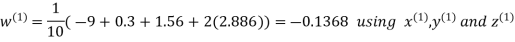

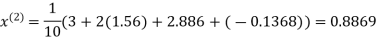
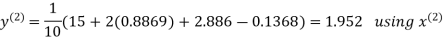
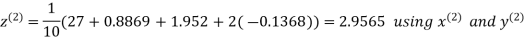
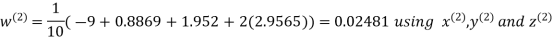

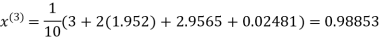
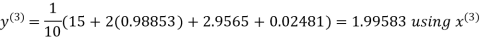
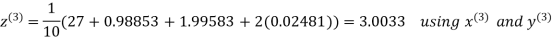
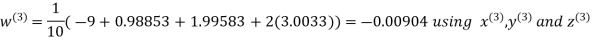

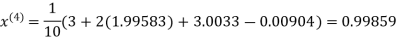
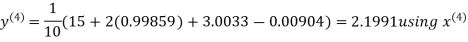
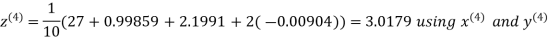
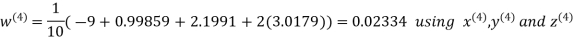

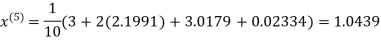
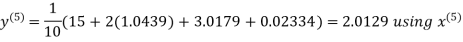
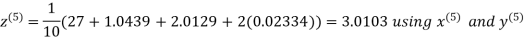
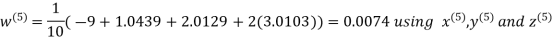
Hence the required solution is 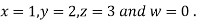
Q(14) Use Euler’s method to find y(0.4) from the differential equation
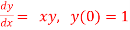 with h=0.1
with h=0.1
Ans-
Given equation 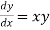
Here 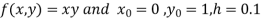
We break the interval in four steps.
So that 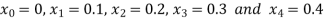
By Euler’s formula
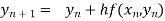 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
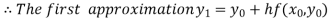
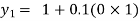
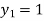
For n=1 in equation (i) we get
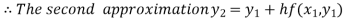
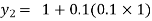
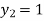 .01
.01
For n=2 in equation (i) we get
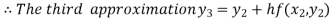
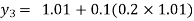
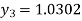
For n=3 in equation (i) we get
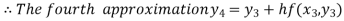
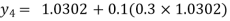
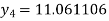
Hence y(0.4) =1.061106.
Q(15)Using Euler’s method solve the differential equation for y at x=1 in five steps
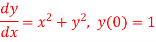
Ans-
Given equation 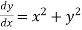
Here 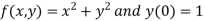
No. of steps n=5 and so that 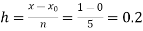
So that 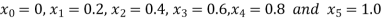
Also 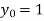
By Euler’s formula
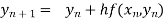 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
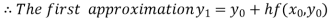
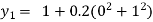
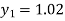
For n=1 in equation (i) we get
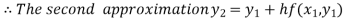
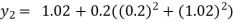
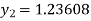
For n=2 in equation (i) we get
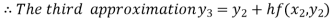
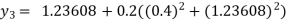
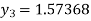
For n=3 in equation (i) we get
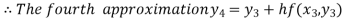
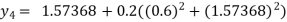
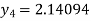
For n=4 in equation (i) we get
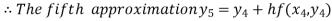
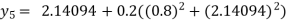
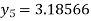
Hence 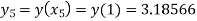
Q(16) Given 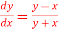 with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
Ans-
Given equation is 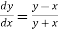
Here 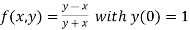
No. of steps n=5 and so that 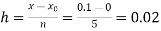
So that 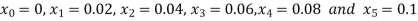
Also 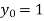
By Euler’s formula
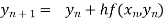 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
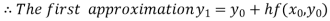
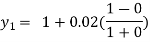
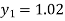
For n=1 in equation (i) we get
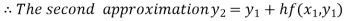
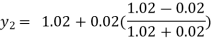
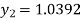
For n=2 in equation (i) we get
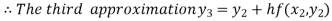
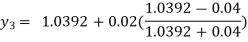
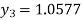
For n=3 in equation (i) we get
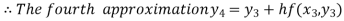
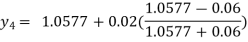
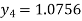
For n=4 in equation (i) we get
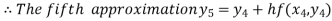
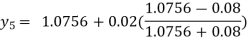
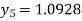
Hence 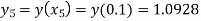
Q(17) Use modified Euler’s method to compute y for x=0.05. Given that

Result correct to three decimal places.
Ans-
Given equation 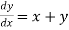
Here 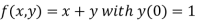
Take h = 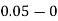 = 0.05
= 0.05
By modified Euler’s formula the initial iteration is
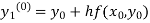
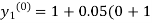 )
)
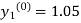
The iteration formula by modified Euler’s method is
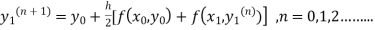 -----(i)
-----(i)
For n=0 in equation (i) we get
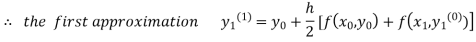
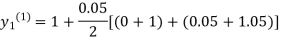
Where 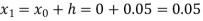 and
and 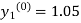 as above
as above
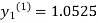
For n=1 in equation (i) we get
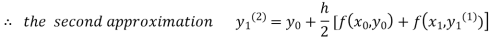
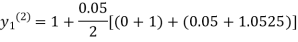
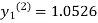
For n=3 in equation (i) we get
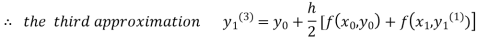
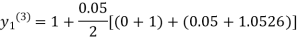
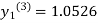
Since third and fourth approximation are equal .
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Q(18) Using modified Euler’s method , obtain a solution of the equation
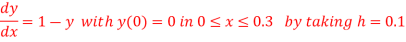
Ans-
Given equation 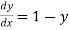
Here 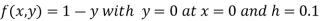
By modified Euler’s formula the initial iteration is
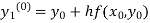
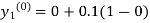
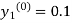
The iteration formula by modified Euler’s method is
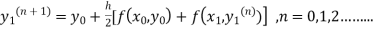 -----(i)
-----(i)
For n=0 in equation (i) we get
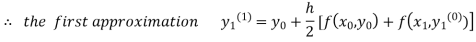
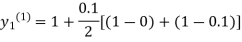
Where 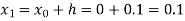 and
and 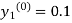 as above
as above
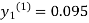
For n=1 in equation (i) we get
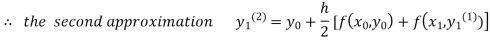
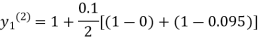
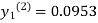
For n=2 in equation (i) we get
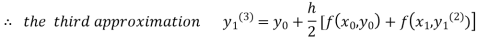
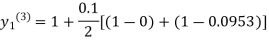
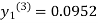
For n=3 in equation (i) we get
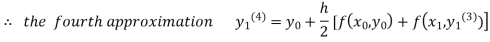
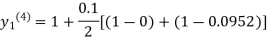
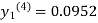
Since third and fourth approximation are equal.
Hence y=0.0952 at x=0.1
To calculate the value of  at x=0.2
at x=0.2
By modified Euler’s formula the initial iteration is
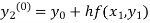
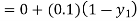
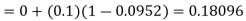
The iteration formula by modified Euler’s method is
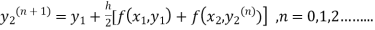 -----(ii)
-----(ii)
For n=0 in equation (ii) we get
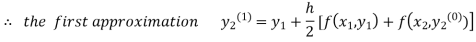
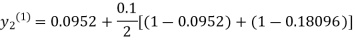
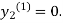 1814
1814
For n=1 in equation (ii) we get
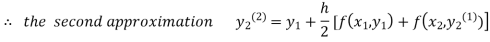
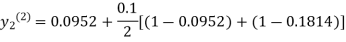
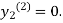 1814
1814
Since first and second approximation are equal .
Hence y = 0.1814 at x=0.2
To calculate the value of 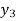 at x=0.3
at x=0.3
By modified Euler’s formula the initial iteration is
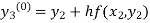
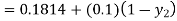
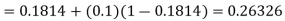
The iteration formula by modified Euler’s method is
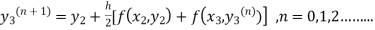 -----(iii)
-----(iii)
For n=0 in equation (iii) we get
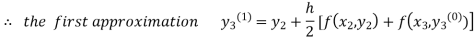
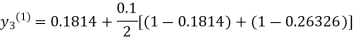
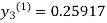
For n=1 in equation (iii) we get
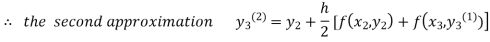
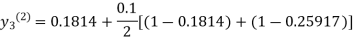
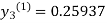
For n=2 in equation (iii) we get
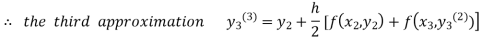
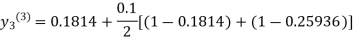
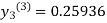
For n=3 in equation (iii) we get
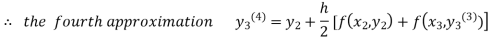
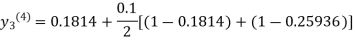
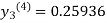
Since third and fourth approximation are same.
Hence y = 0.25936 at x = 0.3
Q(19) Use Runge-Kutta method to find y when x=1.2 in step of h=0.1 given that
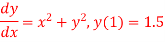
Ans-
Given equation 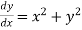
Here 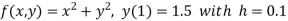
Also 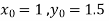
By Runge-Kutta formula for first interval
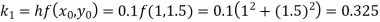
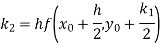
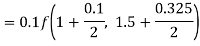
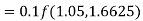
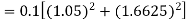
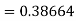
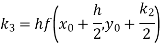
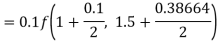
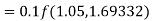
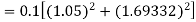
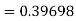
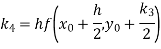
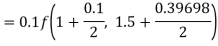
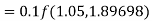
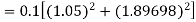
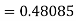
Again 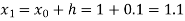
A fourth order Runge-Kutta formula:
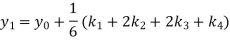

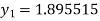
To find y at 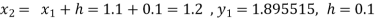
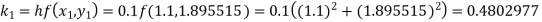
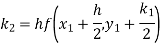
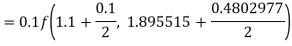
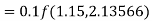
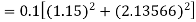
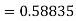
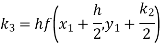
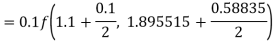
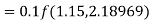
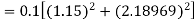
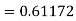
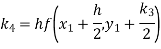
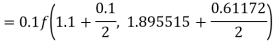
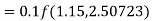
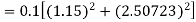
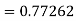
A fourth order Runge-Kutta formula:
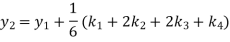

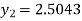
Q(20) Apply Runge-Kutta fourth order method to find an approximate value of y for x=0.2 in step of 0.1, if

Ans-
Given equation 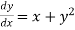
Here 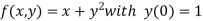
Also 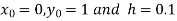
By Runge-Kutta formula for first interval
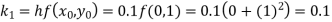
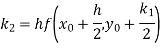
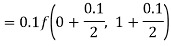
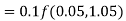
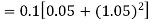
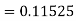
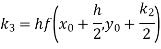
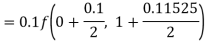
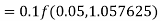
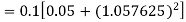
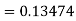
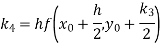
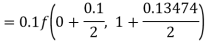
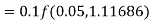
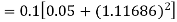
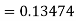
A fourth order Runge-Kutta formula:
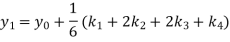
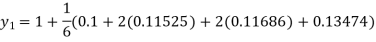
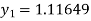
Again 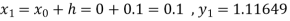
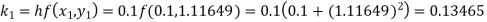
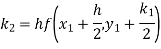

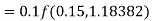
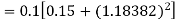
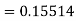
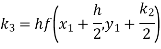

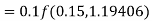
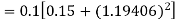
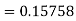
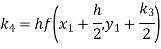

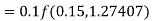
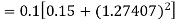
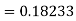
A fourth order Runge-Kutta formula:
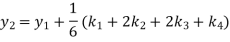
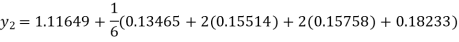
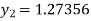
Q(21)Using Runge-Kutta method of fourth order, solve
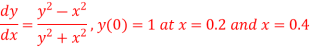
Ans-
Given equation 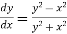
Here 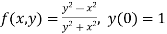
Also 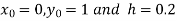
By Runge-Kutta formula for first interval
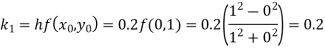
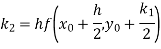
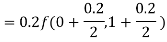
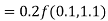
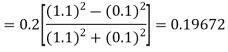
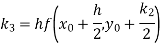
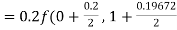 )
)
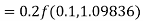
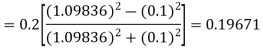
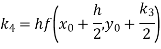
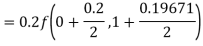
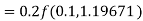
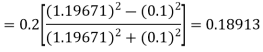
A fourth order Runge-Kutta formula:
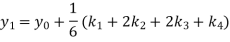
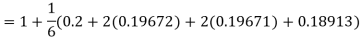
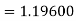
Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 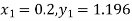
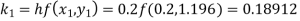
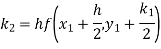
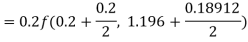
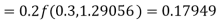
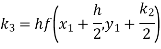
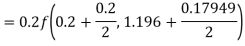
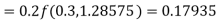
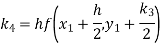
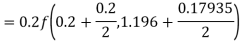
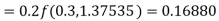
A fourth order Runge-Kutta formula:
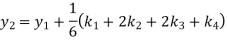
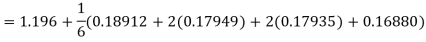
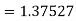
Hence at x = 0.4 then y=1.37527