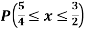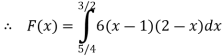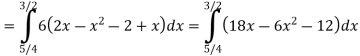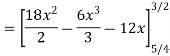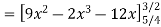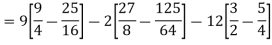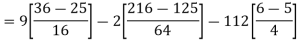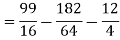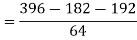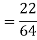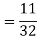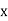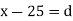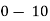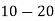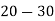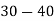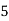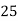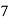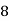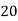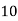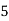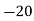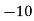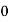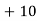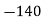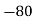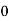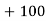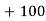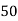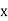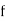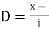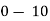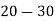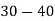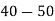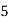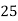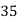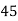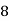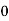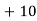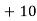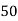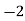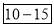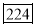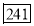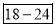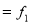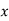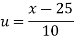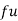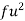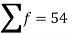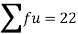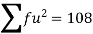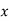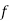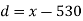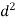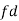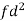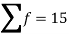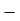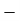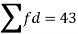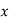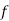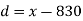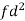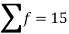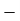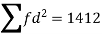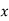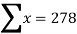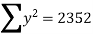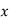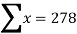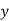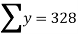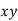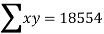UNIT 3
Statistics and Probability
Q(1) Find the arithmetic mean for the following distribution:
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
Ans-
Let assumed mean (a) = 25
Class | Mid‐value
| Frequency |
|
|
40— 50 |
|
|
|
|
Total |
|
|
|
|
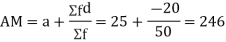
Q(2) Find the arithmetic mean of the data given in last example by step deviation method
Ans-
Solution: Let 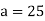
Class | Mid‐value
| frequency
|
|
|
|
|
|
|
|
Total |
|
|
|
|
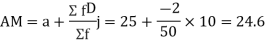
Q(3) Find the median of 6, 8, 9, 10, 11, 12, and 13.
Ans-
Solution:
Total number of items 
The middle item 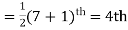
Median  Value of the 4th item
Value of the 4th item 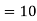
For grouped data, Median 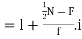
where 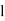 is the lower limit of the median class,
is the lower limit of the median class, 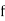 is the frequency of the class,
is the frequency of the class, 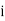 is the width ofthe class‐interval,
is the width ofthe class‐interval, 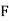 is the total ofall the preceding frequencies of the median‐class and
is the total ofall the preceding frequencies of the median‐class and 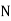 is total frequency ofthe data.
is total frequency ofthe data.
Q(4) Find the value of Median from the following data:
No. of days for which absent (less than) |
|
|
|
|
|
|
|
|
|
No. of students |
|
|
|
|
|
|
|
|
|
Ans-
Solution: The given cumulative frequency distribution will first be converted into ordinary frequency as under
Class Interval | Cumulative frequency | Ordinary frequency |
0-5 5-10
15-20 20-25 25-35 30-35 35-40 40-45 | 29
465 582 634 644 650 653 655 | 29=29 224-29=195 465-224= 582-465=117 634-582=52 644-634=10 650-644=6 653-650=3 655-653=2 |
Median  size of
size of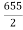 or 327.
or 327.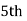 Item
Item
327.  Item lies in 10‐15 which is the median class.
Item lies in 10‐15 which is the median class.
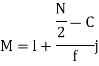
Where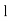 stands for lower limit ofmedian class,
stands for lower limit ofmedian class,
 Stands for the total frequency,
Stands for the total frequency,
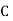 Stands for the cumulative frequency just preceeding the median class,
Stands for the cumulative frequency just preceeding the median class,  stands for class interval
stands for class interval
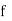 Stands for frequency for the median class.
Stands for frequency for the median class.
Median 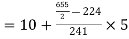
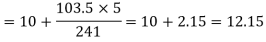
Q(5) Find the mode of the following items:
 .
.
Ans-
6 occurs 5 times and no other item occurs 5 or more than 5 times, hence the mode is 6.
For grouped data, 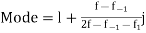
where 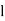 is the lower limit of the modal class,
is the lower limit of the modal class, 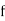 is the frequency of the modal class,
is the frequency of the modal class, 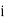 is the width of the class,
is the width of the class, 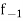 is the frequency before the modal class and
is the frequency before the modal class and  is the frequency after the modal class.
is the frequency after the modal class.
Empirical formula
Mean‐ Mode 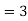 [Mean
[Mean 
Q(6) Find the mode from the following data:
Age | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
Frequency | 6 | 11 | 25 | 35 | 18 | 12 | 6 |
Ans-
Age | Frequency | Cumulative frequency |
0-6 6-12 12-18
24-30 30-36 36-42 | 6 11 25 35
12 6 | 6 17 42 77 95 107 113 |
Mode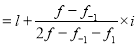
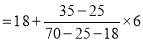

Q(7) Find the geometric mean of 4, 8, 16.
Ans-
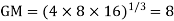 .
.
Q(8) Calculate the harmonic mean of 4, 8, 16.
Ans-
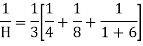
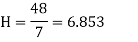
Q(9) Calculate S.D for the following distribution.
Wages in rupees earned per day | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
No. of Labourers | 5 | 9 | 15 | 12 | 10 | 3 |
Ans-
Wages earned C.I | Mid value | Frequency |
|
|
|
52 | 5 | 5 | -2 | -10 | 20 |
153 | 15 | 9 | -1 | -9 | 9 |
25 | 25 | 15 | 0 | 0 | 0 |
35 | 35 | 12 | 1 | 12 | 12 |
45 | 45 | 10 | 2 | 20 | 40 |
55 | 55 | 3 | 3 | 9 | 27 |
Total | - |
|
|
|
|
Using formula,
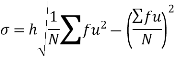
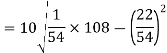
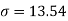
Q(10) Fluctuations in the aggregate of marks obtained by two groups of students are given below.
Group A | 518 | 519 | 530 | 530 | 530 | 544 | 518 | 550 | 527 | 527 | 531 | 550 | 550 | 529 | 528 |
Group B | 825 | 830 | 830 | 819 | 814 | 814 | 844 | 842 | 826 | 826 | 832 | 835 | 835 | 840 | 840 |
Ans-
Solution:
First we represent the data in frequency distribution from group A
|
|
|
|
|
|
518 519 527 528 529 530 531 542 544 550 | 2 1 2 1 1 2 1 1 1 3 | -12 -11 -3 -2 -1 0 1 12 14 20 | 144 121 9 4 1 0 1 144 196 400 | -24 -11 -6 -2 -1 0 1 12 14 60 | 288 121 18 4 1 0 1 144 196 1200 |
Total |
|
|
|
|
|
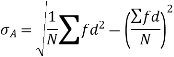
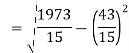

For group B,
|
|
|
|
|
|
814 819 825 826 830 832 835 840 842 844 | 2 1 1 1 2 1 2 2 2 1 | -16 -11 -5 -4 0 2 5 10 12 14 | 256 121 25 16 0 4 25 100 144 196 | -24 -11 -6 -2 -1 0 1 12 14 60 | 288 121 18 4 1 0 1 144 196 1200 |
Total |
|
|
|
|
|
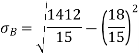
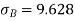
Q(11)Calculate coefficient variation for the following frequency distribution.
Wages in Rupees earned per day | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
No. of Labourers | 5 | 9 | 15 | 12 | 10 | 3 |
Ans-
Solution:
We already calculated
 ….. (refer last Ex.)
….. (refer last Ex.)
Now, A.M 
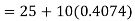
A.M 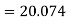
 Coefficient of Variation
Coefficient of Variation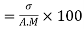
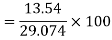
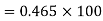

Q(12) Refer Question – 10 Calculate the coefficient of variation
Ans-
As we calculate,
σ for Group A σA=11.105
Now A.M 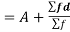
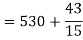
A.M 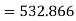
Coefficient of Variation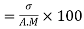

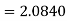
Same for Group B,
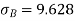
Now, 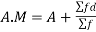
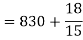
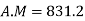
Coefficient of Variation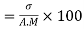
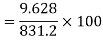
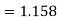
Q(13) If X and Yare uncorrelated random variables,  the
the  of correlation between
of correlation between 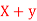 and
and 
Ans-
Let 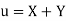 and
and 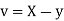
Then 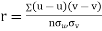
Now 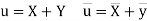
Similarly 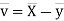
Now 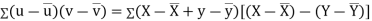


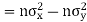
Also 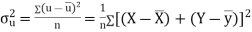
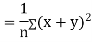
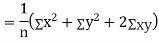
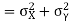 (As
(As 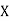 and
and 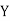 are not correlated, we have
are not correlated, we have 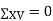 )
)
Similarly 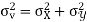
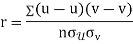
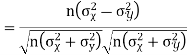
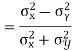
Q(14) Find the correlation  between x and
between x and  , when the lines ofregression are:
, when the lines ofregression are: 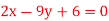 and
and 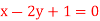
Ans-
Let the line of regression ofx on 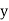 be
be 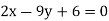
Then, the line ofregression ofy on 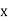 is
is 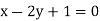
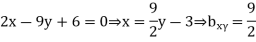
and
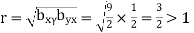 which is not possible. So our choice of regression line is incorrect.
which is not possible. So our choice of regression line is incorrect.
The regression line ofx on 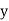 is
is 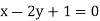
And, the regression line ofy on 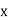 is
is 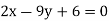
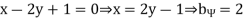
And 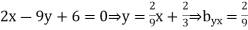
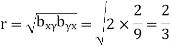
Hence the correlation coefficient between 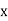 and
and 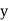 is
is 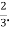
Q(15) The following regression equations were obtainedfrom a correlation table:
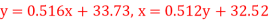
Find the value of
(a) The correlation coefficient,
(b) The mean 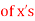 and
and
(c) The mean of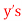
Ans-
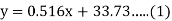
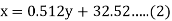
(a) From (1), 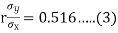
(b) From (2), 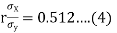
From (3) and (4)


Coefficient of correlation 
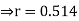
(b) (1) and (2) pass through the point 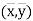 .
.
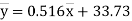 (5)
(5)
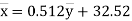 (6)
(6)
On solving (5) and (6), we get
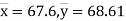
Q(16)Discuss the Reliability of Regression Estimates:
A | 45 | 38 | 59 | 64 | 72 |
B | 60 | 48 | 82 | 93 | 45 |
Ans-
For A,
| 45 | 38 | 59 | 64 | 72 |
|
| 2025 | 1444 | 3481 | 4096 | 5184 |
|
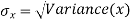
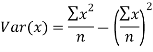

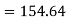
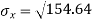
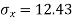
For B,
| 60 | 48 | 82 | 93 | 45 |
|
| 2025 | 1444 | 3481 | 4096 | 5184 |
|
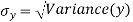
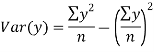

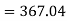
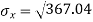

Now,
| 45 | 38 | 59 | 64 | 72 |
|
| 60 | 48 | 82 | 93 | 45 |
|
| 2700 | 1824 | 4838 | 5952 | 3240 |
|

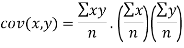
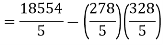
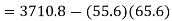
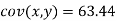
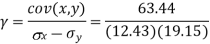
The standard error of Regression of estimates of y on x is
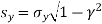
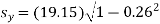

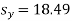
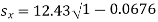 …. (Standard error of Regression of estimates of y on x is)
…. (Standard error of Regression of estimates of y on x is)
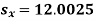
Q(17) A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.
Ans-
We consider the following events:
A: Selected item comes from A.
B: Selected item comes from B.
D: Selected item is defective.
We are looking for . We know:
. We know:
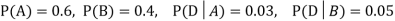
Now,
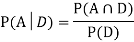
So we need
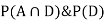
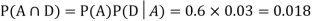
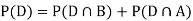
Since, D is the union of the mutually exclusive events 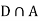 and
and  (the entire sample space is the union of the mutually exclusive events A and B)
(the entire sample space is the union of the mutually exclusive events A and B)

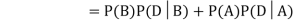
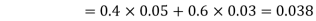
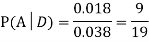
Q(18): Two fair dice are rolled, 1 red and 1 blue. The Sample Space is
S = {(1, 1),(1, 2), . . . ,(1, 6), . . . ,(6, 6)}.Total -36 outcomes, all equally likely (here (2, 3) denotes the outcome where the red die show 2 and the blue one shows 3).
(a) Consider the following events:
A: Red die shows 6.
B: Blue die shows 6.
Find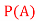 ,
, 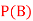 and
and  .
.
Ans-
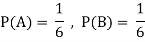

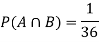
NOTE: 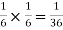 so
so 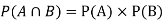 for this example. This is not surprising - we expect A to occur in
for this example. This is not surprising - we expect A to occur in  of cases. In
of cases. In  of these cases i.e. in
of these cases i.e. in 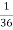 of all cases, we expect B to also occur.
of all cases, we expect B to also occur.
(b) Consider the following events:
C: Total Score is 10.
D: Red die shows an even number.
Find 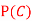 ,
, 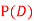 and
and  .
.
Ans-
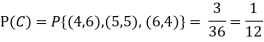
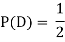
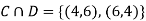
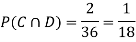
NOTE: 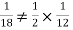 so,
so,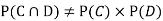 .
.
Why does multiplication not apply here as in part (a)?
Answer: Suppose C occurs: so the outcome is either (4, 6), (5, 5) or (6, 4). In two of these cases, namely (4, 6) and (6, 4), the event D also occurs. Thus
Although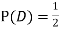 , the probability that D occurs given that C occurs is
, the probability that D occurs given that C occurs is  .
.
We write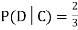 , and call
, and call 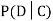 the conditional probability of D given C.
the conditional probability of D given C.
NOTE: In the above example
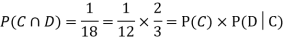
Q(19): Three urns contain 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. If the ball drawn is red find the probability that it is drawn from the first urn.
Ans-
 :The ball is drawn from urnI.
:The ball is drawn from urnI.
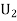 : The ball is drawn from urnII.
: The ball is drawn from urnII.
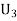 : The ball is drawn from urnIII.
: The ball is drawn from urnIII.
R:The ball is red.
We have to find 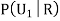

Since the three urns are equally likely to be selected
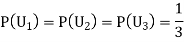
Also,
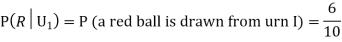
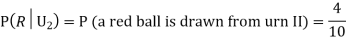
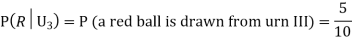
From (i), we have
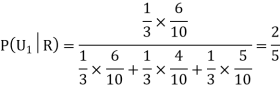
Q(20) . If 
Find (i)  (ii)
(ii) 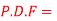 (iii)
(iii) 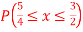
Ans-
Solution:
(i) Condition of P.D.F
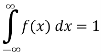
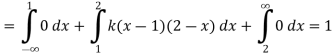
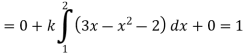

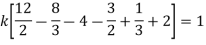
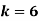
(ii)
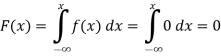
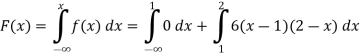
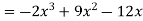
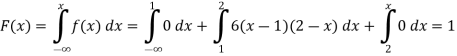
(iii)