Unit 5
Vector Integral Calculus and Applications
Q(1) Evaluate  where F= cos y.i-x siny j and C is the curve y=
where F= cos y.i-x siny j and C is the curve y=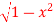 in the xy plane from (1,0) to (0,1)
in the xy plane from (1,0) to (0,1)
Ans-
The curve y=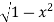 i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
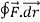 =
= 
= 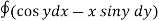
=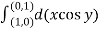 =-1
=-1
Q(2). Evaluate 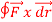 where
where  = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
Ans-
F x dr = 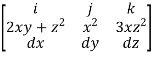
Put x=t, y=t2, z= t3
Dx=dt ,dy=2tdt, dz=3t2dt.
F x dr = 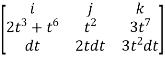
=(3t4-6t8) dti – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
= t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
=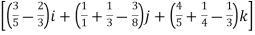
=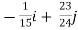 +
+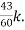
Que(3) Prove that ͞͞͞F = [y2 cos x +z3] i+(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for͞͞͞F (ii) the work done in moving an object in this field from (0, 1, -1) to (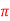 / 2,-1, 2)
/ 2,-1, 2)
Ans-
(a) The fleld is conservative if cur͞͞͞͞͞͞F = 0.
Now, curl͞͞͞F = 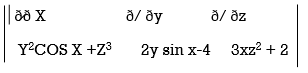
; Cur  = (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2 cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =
(y2 cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k = 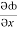 i +
i + 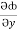 j +
j + 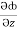 k
k
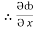 = y2 cos x + z3,
= y2 cos x + z3, 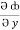 = 2y sin x – 4,
= 2y sin x – 4, 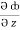 = 3xz2 + 2
= 3xz2 + 2
Now, 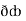 =
= 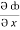 dx +
dx +  dy +
dy + 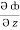 dz
dz
= (y2 cos x + z3) dx +(2y sin x – 4)dy + (3xz2 + 2)dz
= (y2 cos x dx + 2y sin x dy) +(z3dx +3xz2dz) +(- 4 dy) + (2 dz)
=d(y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =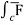 .d ͞r
.d ͞r
=  dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
= 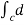 (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z ]( 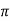 /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4 ] – { - 4 – 2} =4
+ 4 + 4 ] – { - 4 – 2} =4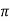 + 15
+ 15
Q(4) Evaluate 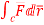 where
where 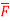 =yz i+zx j+xy k and C is the position of the curve.
=yz i+zx j+xy k and C is the position of the curve.
 = (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
Ans-
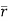 = (a cost)i+(b sint)j+ct k
= (a cost)i+(b sint)j+ct k
The parametric eqn. of the curve are x= a cost, y=b sint, z=ct (i)
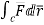 =
=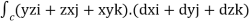
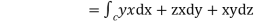
Putting values of x,y,z from (i),
dx=-a sint
dy=b cost
dz=c dt
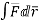 =
=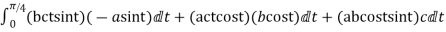
=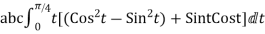
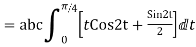
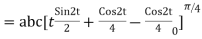
=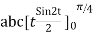 =
= 
Q(5) Find the circulation of 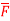 around the curve C where
around the curve C where 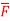 =yi+zj+xk and C is circle
=yi+zj+xk and C is circle 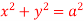 .
.
Ans-
Parametric eqn of circle are:
x=a cos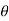
y=a sin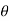
z=0
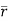 =xi+yj+zk = a cos
=xi+yj+zk = a cos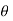 i + b cos
i + b cos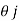 + 0 k
+ 0 k
d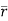 =(-a sin
=(-a sin i + a cos
i + a cos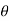 j)d
j)d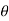
Circulation =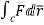 =
=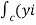 +zj+xk). d
+zj+xk). d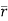
=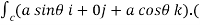 -a sin
-a sin i + a cos
i + a cos j)d
j)d
=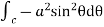 =
= 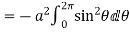
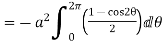
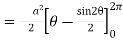
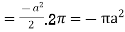
Q(6) Verify green’s theorem for 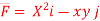 and C is the triangle having verticles A (0,2 ) , B (2,0 ) , C (4,2 ).
and C is the triangle having verticles A (0,2 ) , B (2,0 ) , C (4,2 ).
Ans-
By green theorem.
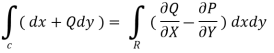
Here ,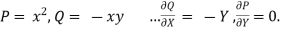
(a) Along AB , since the equation of AB is
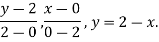
Putting 
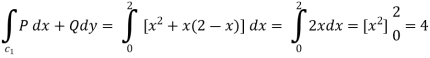
Along BC , since the equation of BC , 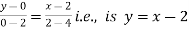 .
.
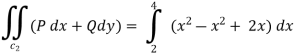
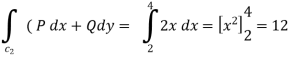
Along CA , since the equation of CA, is y = 2 , dy = 0.
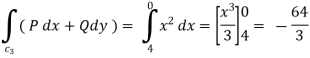
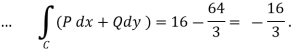
(b) 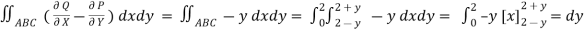
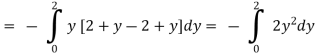
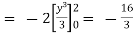 .
.
From (1) and (2) , the theorem is verified .
Q(7) Evaluate by Green ‘s theorem 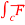 = - xy (xi –yj) and c is r= a (1+ cos
= - xy (xi –yj) and c is r= a (1+ cos  )
)
Ans-
By Green’s Theorem ,  ) dx dy
) dx dy
Now, 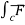 .dṝ =
.dṝ = 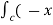 2yi + xy2 j ) . (d xi + dy j) =
2yi + xy2 j ) . (d xi + dy j) = 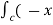 2y dx + xy2dy )
2y dx + xy2dy )
By comparison p= - x2y, Q = xy2
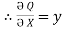 2,
2,  = - x2
= - x2 2 + x2) dx dy
2 + x2) dx dy
To evaluate the integral , we put x = r cos  , y = r sin
, y = r sin 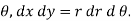 for the cardioid r = a ( 1 + cos
for the cardioid r = a ( 1 + cos 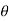 ), we take the integral from
), we take the integral from 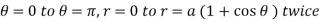
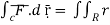 2 .rdr d
2 .rdr d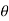 = 2
= 2 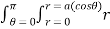 3dr d
3dr d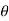
= 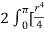 ]a ( 1 + cos
]a ( 1 + cos 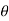 ) dθ =
) dθ = 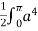 (1+ cos θ)4dθ
(1+ cos θ)4dθ
=8a4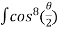 =
= 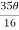 a4
a4
Q(8) Verify Green’s Theorem in the plane for 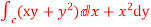 where C is the closed curve of region bounded by y=x and y=
where C is the closed curve of region bounded by y=x and y=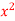 .
.
Ans-
Soln. By Green’s Theorem,
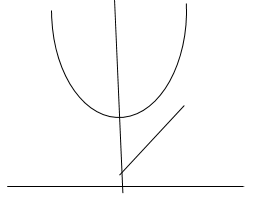
 A(1,1)
A(1,1)
 y=x
y=x y=
y=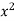
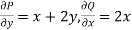 B
B
(a) Along  , y=
, y=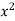 and dy=2x dx and x varies from 0 to 1.
and dy=2x dx and x varies from 0 to 1.
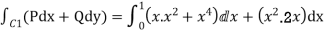
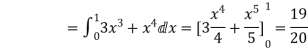
 Along
Along 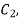 y=x and dy=dx and x varies from 1 to 0.
y=x and dy=dx and x varies from 1 to 0.
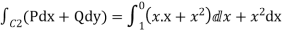
=
=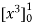 = 1
= 1
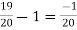 = L.H.S.
= L.H.S.
RHS=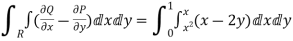
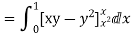
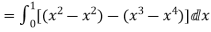
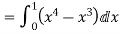
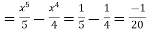
Q(9) Use divergence theorem to show that 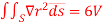 where Sisanyclosed surface enclosing a volume V.
where Sisanyclosed surface enclosing a volume V.
Ans-
By divergence theorem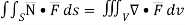
Here ,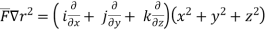
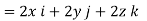
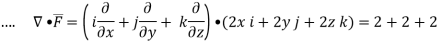
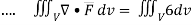 = 6V
= 6V
Q(10 )Show that 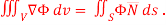
Ans-
By divergence theorem, 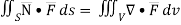 ..…(1)
..…(1)
Comparing this with the given problem let
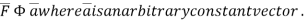
Hence, by (1)
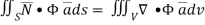 ………….(2)
………….(2)
Now ,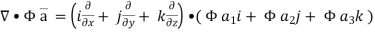
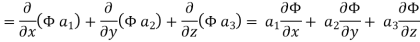
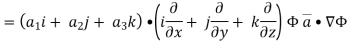
Hence, from (2),We get,
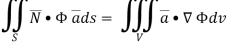

Q(11) Show that
Ans-
We have Gauss Divergence Theorem
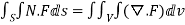
By data, F=

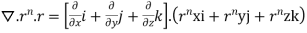
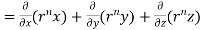
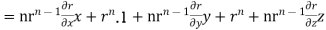
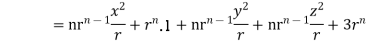
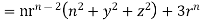
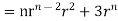

=(n+3)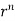

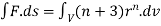
Q(12) Prove that 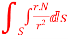 =
=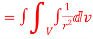
Ans-
By Gauss Divergence Theorem,
 =
=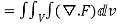
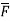 =
=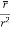 =
=
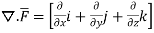 .[
.[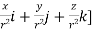
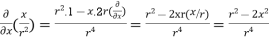


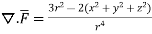 =
= 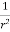
Q(13) Use stoke’s theorem to evaluate 
Ans-
We have by stoke’s theorem 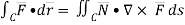
Now ,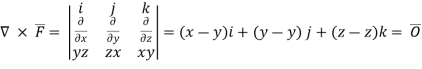
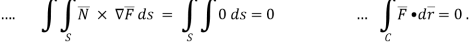
Q(14):- velocity distribution for a fluid flow is given by
 find the equation of
find the equation of
Stream line passing through the point (1,1,2)
Ans:-
the diffential equation of stream line are given by
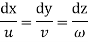
Putting for u,v,w we get

These are two independent equations, consider
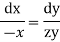
Integrating 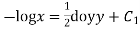 -------1
-------1
As stream the passes through (1,1,2)
Put x=1 , y=1 in eq. 1
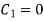
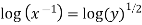
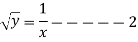
Consider now, 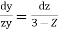
Integrating gives , 
Putting  we get
we get 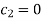
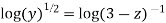
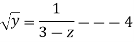
Equation 2 &4 together represent curve of intersection of surface
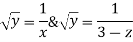
Which represents the stream line
Q(15):- if the velocity of an incompressible fluid at (x,y,z) is given by

Where 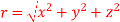
Then determine the stream line at motion
Ans:-
equation of stream lines are given by
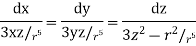
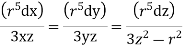
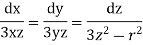
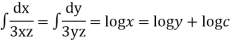

Similarly
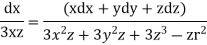
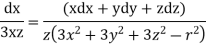


Integrating , 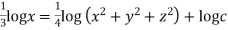

Eq 1 & 2 together represents stream line
Que(16)given the velocity fields

What is the acceleration of a particle at (3,0,2) at time t=1
Ans :- we have u=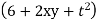 , V =
, V = 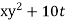 , W =25
, W =25
The component is given by

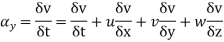
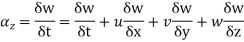


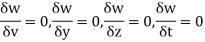
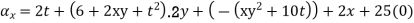
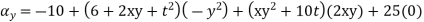
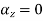
Substituting x=3, y=0 & z=2 &t=1
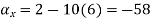
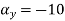
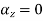
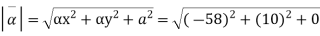
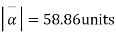
Q(17):- a liquid is in equilibrium under the action of field  per unit mass given by
per unit mass given by
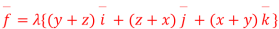
Find the pressure at any point on the field
Ans:- let v be the force potential
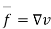
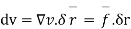


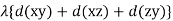
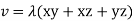
From the Bernoullis eq
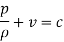
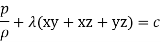
Which gives pressure at any point