Unit 2
Fluid Kinematics & Fluid Dynamics
Q1. Explain mathematical expression of velocity and acceleration in Cartesian form.
Ans- Velocity expression-
Let V is the resultant velocity at any point in a fluid flow.
Let u, v, and w are its components in x, y, and z directions.
The velocity components are functions of space coordinates and time. Mathematically, the velocity components are given as
u = f1(x, y, z, t)
v = f2(x, y, z, t)
w = f3(x, y, z, t)
and Resultant velocity, v = 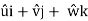
→ |v| = 
Acceleration expression-
Let ax, ay, and az are the total acceleration in x, y, and z direction respectively. Then by the chain rule of differentiation, we have
ax = 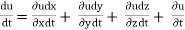
but 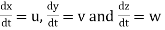
ax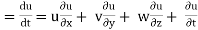
similarly, ay 
az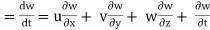
Acceleration vector a = axi + ayj + azk
= 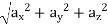
Q2. Explain in detail Classification of flows.
Ans- Classification of flows
1) Steady and Unsteady flows
Steady flow – The type of flow in which the fluid characteristics like velocity, pressure, density, etc. at a point do not change with time is called steady flow.
Example: Flow-through prismatic or non-prismatic conduct at a constant flow rate Q m3/s is steady.
Mathematically, 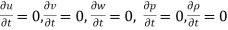
Unsteady flow: It is that type of flow in which the velocity, pressure,2 or density at a point change w.r.t. time.
E.g.: the flow in a pipe whose value is being opened or closed gradually.
Mathematically, 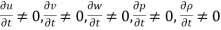
2) Uniform and Non-uniform Flows
Uniform flow – The type of flow, in which the velocity at any given time does not change with respect to space is called uniform flow.
E.g.: Flow through a straight prismatic conduit.
Mathematically, 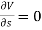 when t = constant
when t = constant
Non-uniform flow – It is the type of flow in which the velocity at any given time changes with respect to space.
E.g.: Flow-through non-prismatic conduit.
Mathematically, 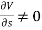 when t = constant
when t = constant
3) One, two & Three-dimensional flow
One dimensional flow – it is that type of flow in which the flow parameter such as velocity is a function of time and one space coordinate.
E.g.: Flow in a pipe where average flow parameters are considered for analysis.
Mathematically, u = f(x), v = 0 & w = 0
Two-dimensional Flow – The flow in which the velocity is a function of time and two rectangular space coordinates is called two-dimensional flow.
E.g.: Flow between parallel plates of infinite extent.
Mathematically, u = f1(x,y) v = f2(x,y) & w = 0
Three-dimensional flow – It is the type of flow in which the velocity is a function of time and three mutually perpendicular directions.
E.g.: Flow in a converging or diverging pipe or channel.
Mathematically, u = f1(x,y,z) v = f2(x,y,z) & w = f3(x,y,z)
4) Rotational and Irrotational Flows
Rotational Flow -A flow said to be rotational if the fluid particles while moving in the direction of flow rotate about their mass centers.
E.g.; Motion of liquid in a rotating tank.
Irrotational flow - A flow said to be rotational if the fluid particles while moving in the direction of flow do not rotate about their mass centers.
E.g.: Flow above a drain hole of a stationary tank or a water basin.
5) Laminar and Turbulent Flows
Laminar Flow – A Laminar flow is one in which paths taken by the individual particles do not cross one another and move along a well-defined path.
E.g.: Flow of blood in veins and arteries.
Turbulent Flow – A turbulent flow is that flow in which fluid particles move in a zig-zag way.
E.g.: High velocity flows in a conduit of large size.
6) Compressible & Incompressible Flow
Compressible Flow – It is that type of Flow in Which the density (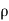 ) of the fluid changes from point to point.
) of the fluid changes from point to point.
E.g.: Flow of gases through orifices, nozzles, gas turbines, etc.
Mathematically, 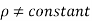
Incompressible Flow – It is the type of flow in which density is constant for the fluid flow. Liquids are generally considered flowing incompressible.
E.g.: subsonic aerodynamics.
Mathematically, 
7) Subcritical, Critical & Supercritical Flow
Subcritical flow– When Froude’s number is less than one the flow is known as subcritical flow.
Mathematically, Fr 
Critical flow– When Froude’s number is equal to one the flow is known as subcritical flow.
Mathematically, Fr 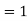
Supercritical flow– When Froude’s number is more than one the flow is known as subcritical flow.
Mathematically, Fr 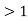
Q3. Definition of 1) Streamline 2) Stream tube 3) Path line 4) Streak line 5) Control volume
Ans- 1) Streamline
A streamline may be defined as an imaginary line within the flow so that the tangent at any point on it indicates the velocity at that point.
2) Stream tube
A stream tube is a fluid mass bounded by a group of streamlines. The contents of the stream tube are known as current filaments. Examples:- Pipes & nozzles.
3) Path line
A path line is a path followed by a fluid particle in motion. A path line shows the direction of a particular particle as it moves ahead.
4) Streak line
A streak line is a curve which gives an instantaneous time picture of the location of the fluid particles, which have passed through a given point
5) Control volume
A definite volume with fixed boundary shape in space along with fluid flow passage is called control volume & the boundary of his volume is known as the control surface.
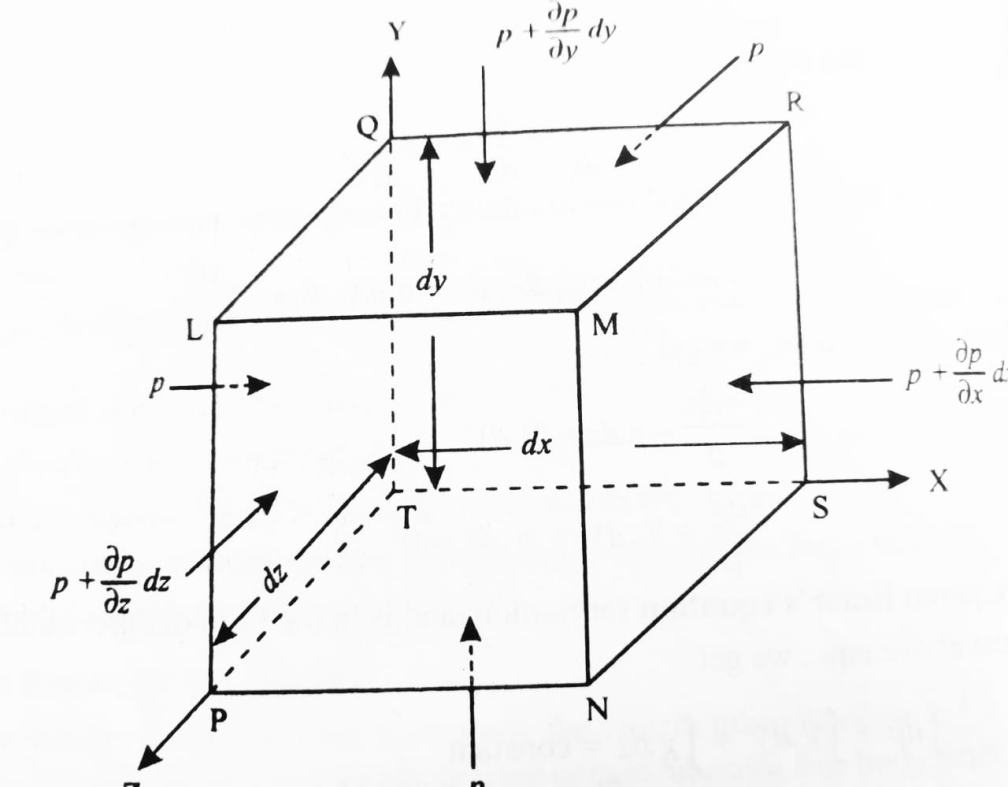
Q4. Explain the Equation of continuity for 3-D flow in Cartesian co-ordinates.
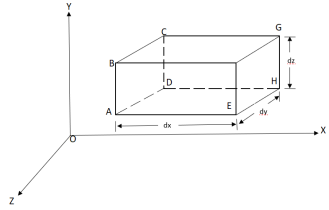
Ans- Consider a fluid element (control volume)- parallelepiped with sides dx, dy, and dz as shown in fig.
Let, 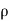 = Mass density of the fluid at a particular instant
= Mass density of the fluid at a particular instant
u, v, w= components of velocity of flow entering the three faces of the parallelepiped.
Rate of Mass of fluid entering the face ABCD
= 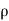 X velocity in x-direction X area of ABCD
X velocity in x-direction X area of ABCD
=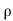 u dy dz
u dy dz
Rate of Mass of fluid leaving the lace FEGH
= 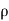 u dy dz +
u dy dz + 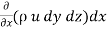
:. Mass accelerated per unit time, due to flow in x-direction
=  u dy dz –[
u dy dz –[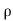 u+
u+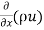 dx]dydz
dx]dydz
= - -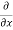 (
(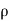 u) dx dy dz
u) dx dy dz
Similarly, the gain in fluid mass per unit time in the parallelepiped due to flow in Y and Z- direction.
= 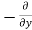 (
(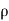 v) dx dy dz ……… (in Y- direction)
v) dx dy dz ……… (in Y- direction)
= 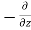 (
(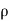 w) dx dy dz ……… (in Z- direction)
w) dx dy dz ……… (in Z- direction)
The total gain in fluid mass per unit for fluid along three co-ordinate axes
= -[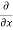 (
(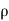 u) +
u) +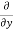 (
(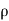 v) +
v) +  (
(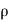 w)] dx dy dz …………1
w)] dx dy dz …………1
Rate of change of mass of the parallelepiped (control volume)
= 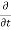 (
(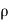 dx, dy dz) ………………….. 2
dx, dy dz) ………………….. 2
From Equation 1& 2
-[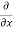 (
(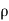 u) +
u) + (
( v) +
v) + (
(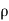 w)] dx dy dz =
w)] dx dy dz = 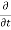 (
(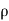 dx dy dz)
dx dy dz)
Simplification and rearrangement of teams would reduce the above expression to
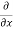 (
( u) +
u) + 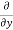 (
(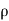 v) +
v) + 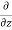 (
(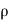 w) +
w) + 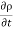 =0
=0
This eq. is the general equation of continuity in three dimensions and applies to any type of flow and for any fluid whether compressible as incompressible
For steady flow (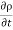 =0) incompressible fluids (
=0) incompressible fluids (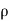 = constant) the equation reduces to
= constant) the equation reduces to
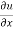 +
+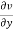 +
+ =0
=0
For two-dimensional flow eq. reduce to
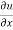 +
+ 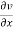 =0
=0
Q5. Explain the Velocity potential, stream function & Components of rotation.
Ans- Velocity Potential Function
The velocity potential is defined as the scalar function of space and time such that its negative derivative with respect to any directions gives the fluid velocity in that direction.
It is denoted by Ø (phi)
Thus, mathematically the velocity potential is defined as
Ø = f(x, y, z, t)
And Ø = f(x, y, z)
u = -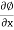
v = -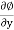
w = -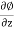
where u, v, and w are the components of velocity in the x, y, and z directions respectively.
The negative sign signifies that Ø decreases with an increase in the values of x, y, and z. in other words, it indicates that the flow is always in the direction of decreasing Ø.
Stream function –
It is defined as the scalar function of space and time such that its partial derivative with respect to any direction gives the velocity component at right angles to that direction.
It is denoted by Ψ (psi) and defined only for two-dimensional flow.
Mathematically, for ready flow, it is defined as Ψ = f(x, y) such that
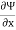 = v
= v
And 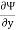 = -u
= -u
Components of rotation-
Rotational component (wz) can be given as-

It shows that Phi exits then, flow will be irrotational.
Q6. Explain Flow net, its uses and limitations.
Ans- Flow net
Use of flow nets
Limitations of flow nets
1) The flow net analysis cannot be applied to the region close to the boundary the effects of viscosity are predominant.
2) In case of a flow of a fluid past a solid body, while the flow net gives a fairly accurate picture of the flow pattern for the upstream part of a solid body, it can give little information concerning the flow conditions at the rare because of separation & eddies.
Q7. Explain Forces acting on fluid mass in motion.
Ans- The motion of the fluid element is influenced by the following forces
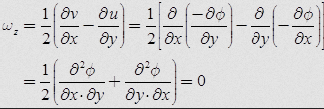
The net pressure force in X direction = p dydz – 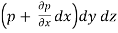
= 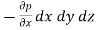
2. Gravity or body force
Let B be the body force per unit mass of fluid having components Bx, By & Bz
In x, y & z directions respectively.
Then, body force acting on the parallelepiped in the direction of X coordinate is = Bx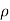 dx dydz
dx dydz
3. Inertia force
The inertia force acting on the fluid mass, along the X coordinates is given by,
Mass x acceleration = 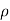 dx dydz
dx dydz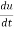
Q7. Explain Modified Bernoulli’s equation.
Ans-
Modified Bernoulli’s equation
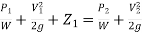 +
+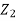 + hL
+ hL
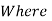 hL = Loss of energy between sections 1 & 2.
hL = Loss of energy between sections 1 & 2.
Q8. Explain in detail HGL and TEL.
Ans- Total energy Line (T.E.L. or E.G.L)
Total head = 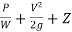
Hydraulic gradient Line (H.G.L)
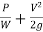
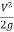
Q9. Does the following velocity component represent physically possible flow?
u = x2y; v = 2zy – xy2; w = x2 – z2y
Ans-
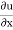 = 2xy
= 2xy
 = 2z – 2xy
= 2z – 2xy
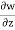 = -2yz
= -2yz
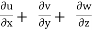 = 2xy + 2z – 2xy – 2yz
= 2xy + 2z – 2xy – 2yz
= 2z – 2yz
≠ 0
Since the continuity equation is not satisfied.
Flow is not physically possible.
Q10. The following represents the following velocity components. Calculate the unknown velocity component so that they satisfy the continuity equations.
u = 2x2; v = 2xyz
Ans-
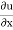 = 4x
= 4x
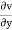 = 2xz
= 2xz
For the continuity equation to be satisfied

4x + 2xz + 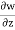 = 0
= 0
 = -4x – 2xz
= -4x – 2xz
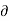 w = (-4x-2xz)
w = (-4x-2xz)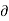 z
z
Integrating
w = -4xz - 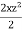
w = -4xz – xz2
Q11.The velocity potential function is given by Ø = 5 (x2 – y2). Calculate velocity components at the point (4, 5)
Ans-
Ø = 5(x2 – y2)
= 5x2 – 5y2
u = 
= -10x
v = 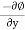
= - (-10y) = 10y
The velocity components at the point (4, 5)
u = -10(4)
= -40 units
v = 10(5)
= 50 units
Q12. A stream function is given by Ψ = 5x – 6y. Calculate the velocity components & also the magnitude & direction of the resultant velocity.
Ans-
Ψ = 5x – 6y
u = 
= -(-6)
= 6 units
v = 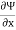
= 5 units
ϴ = 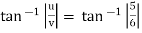
= 39.80˚
Q13. The streamlines is represented by Ψ = x2 + y2. Find its corresponding velocity potential. Determine the velocity and its direction at (2, 2).
Ans-
Ψ = x2 + y2
u = 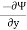
= -2y
v = 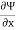
= 2x
At point (2,2)
u = -2(2)
= -4 units
v = 2(2)
= 4 units
V = 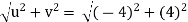
= 5.657 units
ϴ = 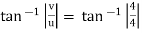
= 45˚
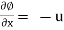
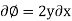
Integrate w.r.to x
Ø = 2yx + f(y) -----------------(1)
Differentiate w.r.to y
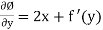
But 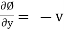
-v = 2x + f’(y)
-2x = 2x + f’(y)
-4x = f’(y)
Integrate w.r.to y
-4xy = f(y)
Put in equation (1)
Ø = 2yx – 4xy
Ø = -2xy
Q14. A flow field is given by v = (x2y)i + (y2z)j – (2xyz + yz2)k. prove that it is a case of possible steady incompressible fluid flow. Calculate velocity & acceleration at the point (2,1,3)
Ans-
u = x2y = (22× 1) = 4 units
v = y2z = (12× 3) = 3 units
w = -2xyz – yz2 = -2 × 2 × 1 × 3 – 1 × 32 = -21 units
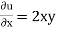
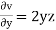

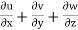
= 2xy + 2yz – 2xy – 2yz
= 0
Hence it is satisfying continuity equation
It is possible case of fluid flow
v = 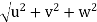
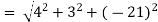
= 21.587 units
ax = 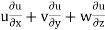
= 4 × 2xy + 3 × x2 – 21 × 0
= 4 × 2 × 2 × 1 + 3 × 22
= 28 units
ay = 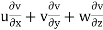
= 4 × 0 + 3 × 2yz – 21 × y2
= 3 × 2 × 1 × 3 – 21 × 22
= - 3 units
az = 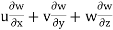
= 4 × -2yz + 3 × (-2xz – z2) – 21(-2xy – 2yz)
= 4 × -2 × 1 × 3 + 3(-2 × 2 × 3 - 32) – 21(-2 × 2 × 1 – 2 × 1 × 3)
= 123 units
a = 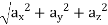
= 
= 126.18 units
Q15. The inlet & throat diameters of horizontal venturimeter are 30cm & 10cm respectively. The liquid flowing throat the meter is water, the pressure intensity at the inlet is 13.734 N/cm2 while the vacuum pressure head at the throat is 37cm of mercury. Find the rate of flow Assume that 4%of the differential head is lost between the inlet & throat. Find also the value Cd for the venturimeter.
Ans-
Given Find Q
d1 =0.3m Cd
d2= 0.1m
p1=13.734 x104N/m2
Vacuum pressure head = - 0.37m of Hg
hf = 4 % of h = 0.04h
A1= x d12 =
x d12 =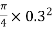 =0.0706m2
=0.0706m2
A2=  x d22=
x d22=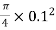 =
=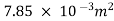
P2 = w *Vacuum pressure head
= (13.6 x 9810) x -0.37
= - 49.37 x103 N/m2
h= 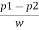 =
=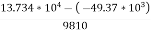
= 19.03 m
hf= 0.04h = 0.04 x 19.032 = 0.7613m
Cd =  =
=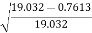 = 0.98
= 0.98
Q=
= 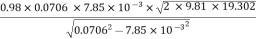
= 0.149 m3/sec
Q16. Find the discharge of water flowing through a pipe 30cm diameter placed in an inclined position where a venturimeter is inserted, having a throat diameter of 15 cm. The difference of pressure between the main & throat is measured by an sp.gr 0.6 in an inverted tube which gives a reading of 30 cm. The loss of head between the main & threat 0.2 times the kinetic head of the pipe.
Ans-
Given find Q
d1 = 0.3 m
d2 = 0.15m
Sm = 0.6
x= 0.3m
hL=0.2 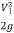
A1 =  * d12 =
* d12 =  * 0.32 = 0.0706m2
* 0.32 = 0.0706m2
A2 =  *d22 =
*d22 =  * 0.152 = 0.0176 m2
* 0.152 = 0.0176 m2
h = x [1- 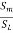 ] = 0.3 [1-
] = 0.3 [1- 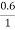 ] = 0.12m
] = 0.12m
Applying Bernoulli’s eqn at section 1& 2
:. 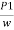 +
+ 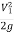 + Z1 =
+ Z1 = +
+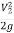 + Z2+ hL
+ Z2+ hL
(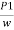 -
- 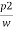 ) + (Z1-Z2) =
) + (Z1-Z2) =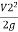 -
- 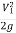 + hL
+ hL
Applying Continuity eqn at section (1) & (2)
A1V1 =A1 V2
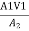 = V2
= V2
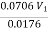 = V2
= V2
:. V2 = 4V1
:. ( -
- 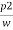 ) + (Z1-Z2) =
) + (Z1-Z2) =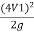 -
-  +
+ 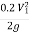
:. h = 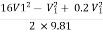
:. 0.12 = 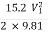
:.V1 = 0.393m/s
:.Q = A1 V1
= 0.0706 x 0.393
= 0.0277 m3/sec