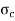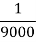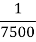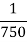Unit - 5
Axially and Eccentric loaded column
Q1) Explain axially loaded column and concept of critical and buckling load.
A2)
2. Concept of critical load and buckling:
The load at which the member just buckle is called as buckling load or crippling load or critical load as shown in fig.
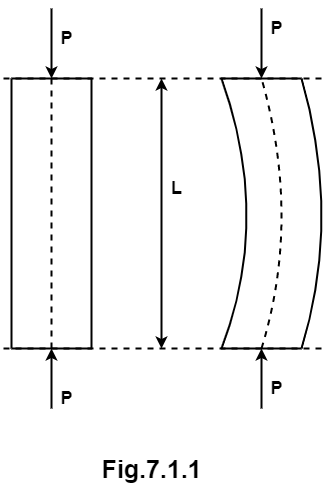
Q2) Explain Euler’s formula for buckling load with hinged ends.
A2) Euler’s formula for buckling load with hinged ends
Consider a column AB of length L with uniform cross-section area A as shown in fig.
Let P = Crippling load at which column is just buckled
Consider a section at a distance x from lower end A
Let y be the lateral displacement at this section.
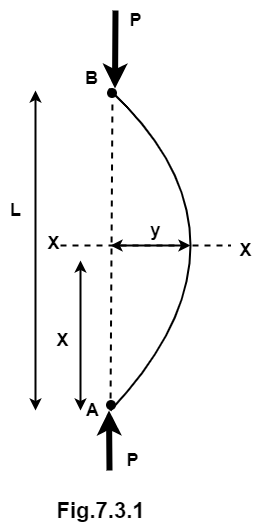
Moment due to critical load P about x, i.e. M = - Py
The bending moment equation at any point is given by EI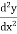
EI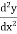 = -Py
= -Py
EI + Py = 0
+ Py = 0
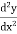 +
+ 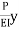 = 0
= 0
The solution of the above differential equation is,
Y = 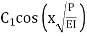 +
+ 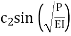
Where 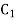 and
and 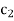 are the integral constants.
are the integral constants.
Applying boundary conditions,
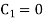
2. At B, x = L, y = 0 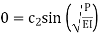
Since  is zero, the
is zero, the  will not be zero.
will not be zero.
If 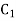 and
and 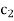 both are zero, the column will not ends.
both are zero, the column will not ends.
 = 0
= 0 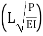 = 0,
= 0,
Considering the least practical value
 =
= 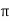
 =
=  P =
P = 
Q3) Explain Rankin’s formula in detail.
A3) Rankin’s Formula:
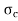

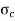
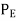
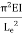
 =
= 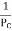 +
+ 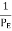 =
= 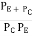
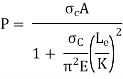
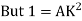


Rankin’s constant is property of the material of the column. Value of rankines constant a and crushing value 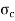 for some materials are given below:
for some materials are given below:
Sr.No. | Material | Crushing Stress | Rankines Constant |
1 | Wrought Iron | 250 MPa |
|
2 | Cast Iron | 550 MPa |
|
3 | Mild Steel | 320 MPa |
|
4 | Timber | 50 MPa |
|
Q4) Explain limitations of Euler’s formula.
A4) Limitations of Euler’s Formula:
Crippling stress 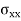 =
= 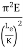


Mathematically, Euler’s formula is applicable,
If crushing stress 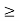 Buckling stress
Buckling stress
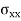

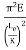
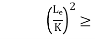
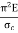


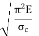
When slenderness ratio is greater then 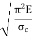 , the Eulers formula is applicable. This is Eulers limitation.
, the Eulers formula is applicable. This is Eulers limitation.
Q5) What is the safe load on column and explain what do you mean by eccentricity?
A5)
2. Eccentricity:
Q6) Explain Direct Load and Eccentric Load in detail
A6)
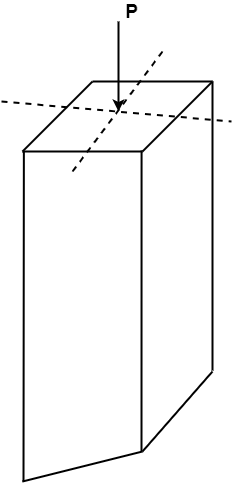
2. Eccentric Loading:
Combined maximum stress = direct stress 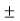 bending stress
bending stress
Maximum stress 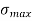 =
=  +
+ 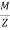 ( Compressive)
( Compressive)
Minimum Stress 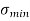 =
=  -
- 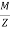 (Tensile)
(Tensile)
Q7) Explain the various loads on chimney.
A7) Chimney:
Let a chimney having cross-sectional area A and Height h subjected to uniform wind pressure 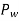
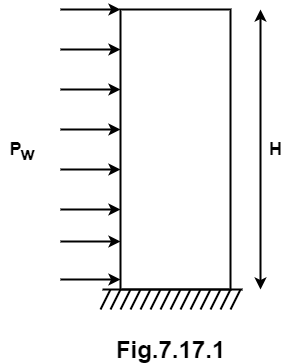
Weight of chimney = W = Weight density  Volume
Volume
Direct stress at base,
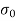 =
= 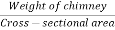
=  =
= 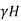
Let wind pressure act on the surface area comes in contact produced bending of structure.
Total wind pressure = Coefficient of wind pressure  Wind pressure
Wind pressure  Projected area
Projected area
P = C 
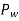
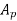
Where C = Coefficient of wind pressure
For plane surface C = 1 and for circular surface C = 2/3
Bending moment at base
M = total wind pressure  distance of its application from base.
distance of its application from base.
= P 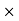

Bending Stress 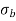 =
=  =
= 
Stress at base
 = Direct stress
= Direct stress 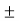 Bending stress =
Bending stress = 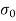

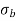
Maximum stress at base 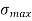 =
= 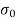 +
+ 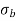
Minimum stress at base  =
=  -
- 
Q8) Explain the effect of various forces on dam.
A8) Dam:
Consider a trapezoidal dam having top width ‘a’ and bottom width ‘b’ and height ‘H’.
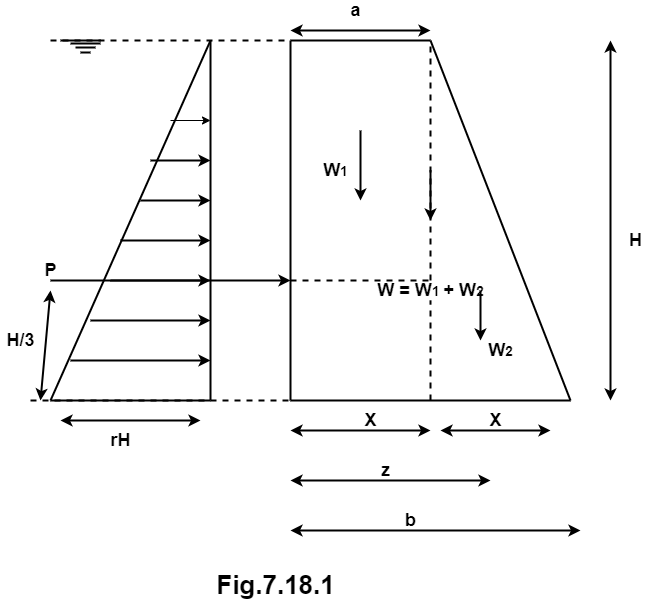
Weight of dam per meter length = Weight density  Area
Area  Length
Length
= 
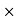
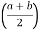 H
H
The weight of the dam act at a distance x from vertical face.
X = 
Consider dam is full of water on its vertical face.
Water pressure at the base p = 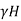
Horizontal force exerted by water = Area of pressure diagram
P = 
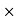 base
base  height =
height = 
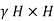
P = 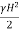
It is acting a distance  from base i.e. at the C.G. of pressure triangle.
from base i.e. at the C.G. of pressure triangle.
Let R be the resultant reaction of Horizontal force P and weight of dam W and passes through point D at a distance Z from A.
Moment about point C
P =  = Wx
= Wx
X = 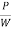
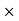

Resultant cuts the base of dam at C from A
Z = 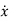 + x
+ x
Eccentricity of weight component
e = Z - 
Moment on the base section
M = W.e
Section modulus of the base section
Z = 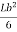 =
=  =
= 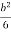
Bending stress 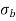 =
= 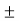
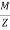 =
= 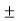
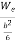
= 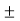
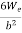
Maximum stress  =
= 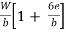
Minimum stress 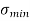 =
= 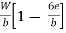
Q9) Explain the effect of self-weight and lateral force in detail.
A9)
2. Effect of self-weight:
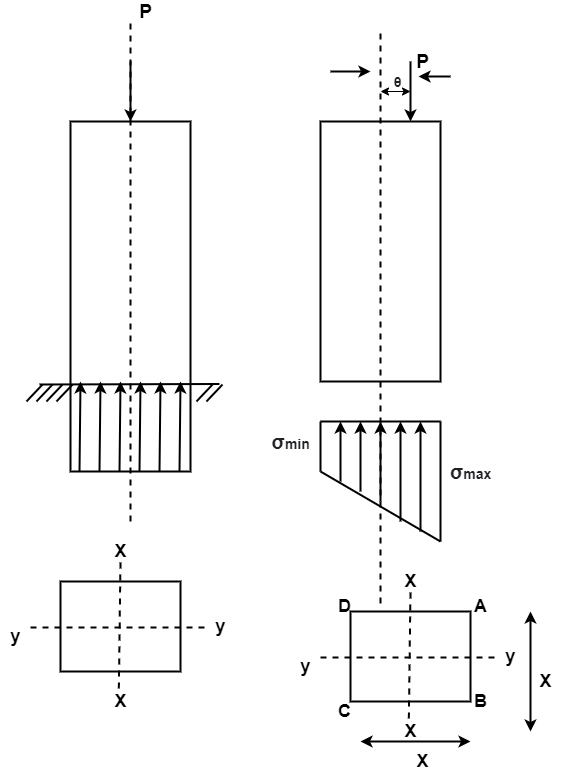
Q10) Explain the stress distribution for rectangular section.
A10) A short column of rectangular section of crosses sectional area A and axial load P is as shown in fig. The intensity of stress is uniform. The stress produced is called as direct stress.
Direct stress 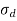 =
= 
In figure, a short column of rectangular cross-section is subjected to an eccentric load P.
Let P = Load acting on the column
e = Eccentricity of the load
b = width of column
d = depth of column
Moment M = P.e
Area A = b  d
d
M.I. of section about an axis through its c.g. and parallel to axis about which the load is eccentric, is
I = 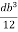
Modulus of section, z = 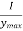 =
= 
Now, Direct stress, 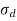 =
= 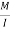
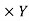 =
= 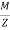
= 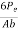
Total stress at extreme fibre
= 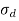
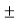
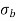
= 
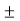
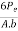 ………… In terms of Eccentricity
………… In terms of Eccentricity
= 
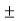
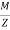 ………….. In terms of Modulus of section
………….. In terms of Modulus of section
Maximum stress at A and B is
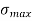 =
= 
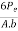
= 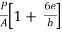 ………… In terms of Eccentricity
………… In terms of Eccentricity
= 
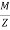 ………….. In terms of Modulus of section
………….. In terms of Modulus of section
Minimum stress at C and D is
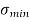 =
= 
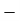
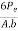
= 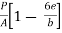 ………… In terms of Eccentricity
………… In terms of Eccentricity
= 
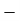
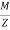 ………….. In terms of Modulus of section
………….. In terms of Modulus of section
Q11) Explain conditions for stress distribution at base.
A11) Condition for stress distribution at base:

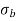
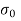
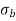
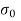

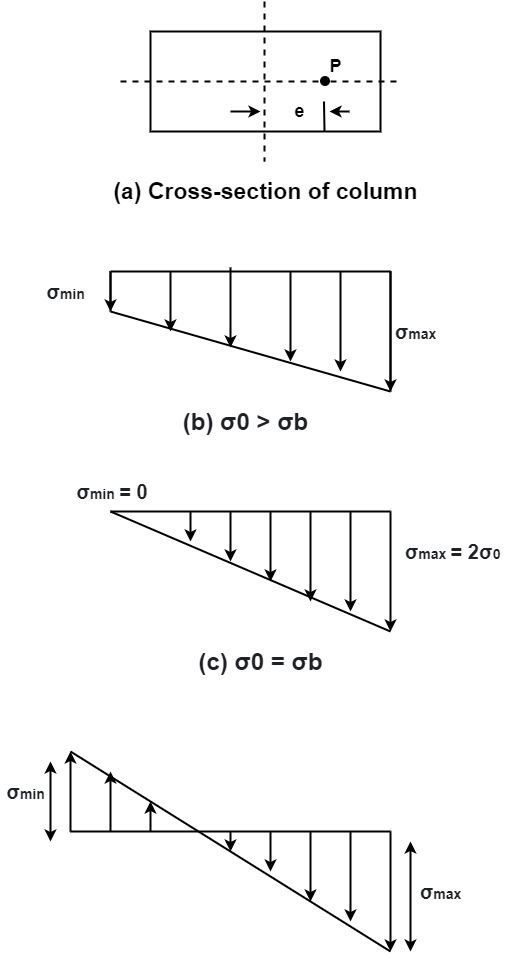
Q12) Explain the condition for no tension.
A12)
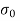
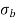
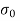
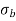
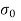
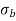

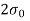
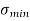
For no tension condition,
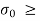
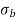


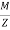


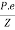

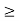

e 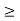

Hence, for no tension condition, eccentricity should be less than or equal to 
2. Rectangular Section
For no tension e =  Area A = bd
Area A = bd
Sectional modulus
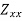 =
= 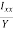 =
= 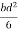
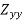 =
= 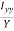 =
= 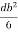
e 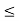
 and e
and e 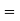

e 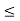
 and e
and e 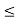
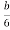
2e 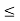
 and 2e
and 2e 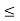
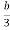
For no tension condition, the load must lies within the middle third shaded area of eccentricity 2e shown in fig. The central shaded portion is known core or kernel of section.
3. Circular Section:
Sectional modulus Z= 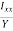
Z = 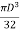
Area e = 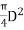
For no tension condition,
e =  =
= 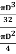
e 

2e 

For no tension developed in the section, the load should be applied within one fourth diameter of diameter of circle as shown by shaded area.
Q13) Find the eccentricity for hollow rectangular section.
A13) Consider a hollow rectangular section with B and D as outer width the thickness and b and d internal width and thickness respectively.
Modulus of section

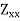 =
= 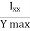 =
= 
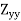 =
= 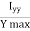 =
= 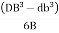
For no tension, e 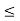

e 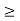
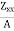 and e
and e 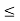

e 
 and e
and e 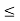
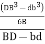
e 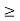
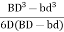 and e
and e 
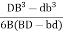
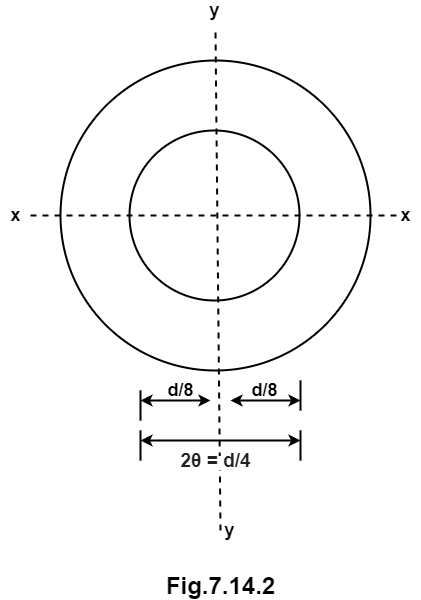
Q14) Find the eccentricity for hollow circular section.
A14) Consider a hollow circular section of external diameter D and internal diameter d.
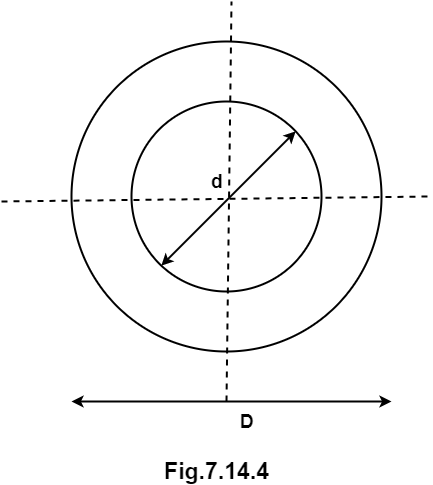
Modulus of section, Z =  =
= 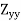 =
=  =
= 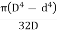
Area of section A = 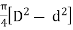
For no tension
e 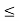

e 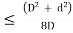
Thus the load can be eccentric on any side of the geometrical centre, by an amount to