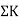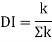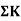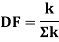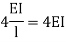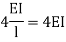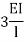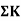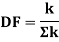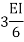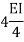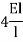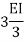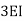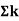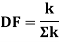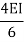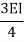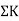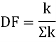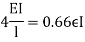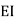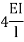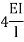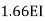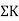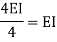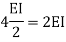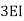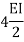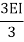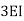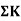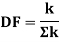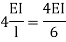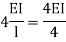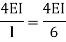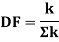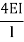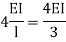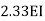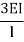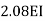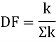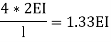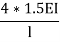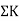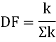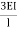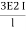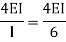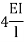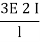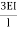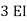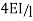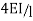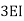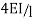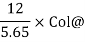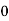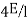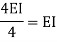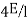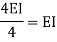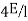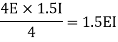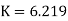Unit - 4
Moment Distribution Method
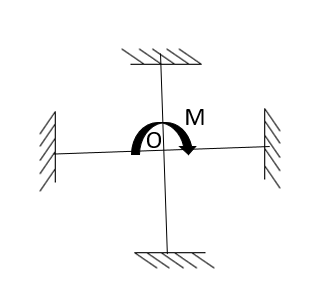
Q1) What is moment distribution method-stiffness factor, carryover factor and distribution factor?
A1) Moment distribution method:
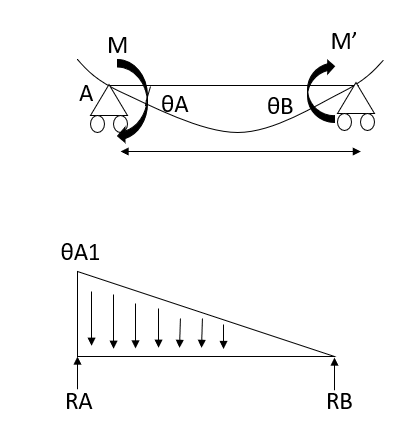
Moment Distribution Method (MDM) is an iteration procedure developed by Cross Hardy in 1930. Therefore, this method is sometimes called as the 'Cross Hardy Method'.
This method starts with the assumption that all points in an indeterminate structure are fixed temporarily against rotation and displacement.
The fixed end moment (FEM) induced by the loading on the spans are written down at each joint.
Then, the joint is released one at a time in succession. Because of the release of joints, unbalanced moments arise at the joints.
These unbalanced moments distributed at the joints in proportion to the stiffness of the members meeting at the joints.
Then these distributed moments are carried over to the far end of the members. Because of the carry-over moments at joints, again unbalanced moments are created which are further distributed and carried over.
In this manner the iteration is performed in successive cycles of operation till the value of joints becomes significant. At this stage, iteration is stopped and the moments at each joint is algebraically summed up.
The sum of the moments at the end of each span at a joint is the required final end moment.
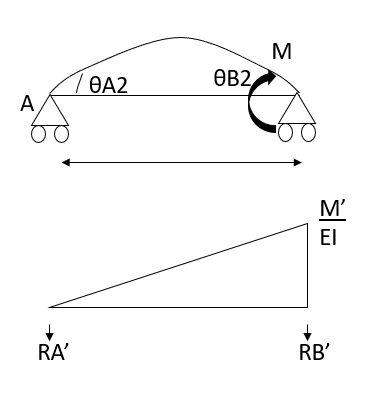
MDM method is quite different than slope deflection method though it is a displacement or stiffness method. Without calculating values of displacement end moments are obtained by successive iteration.
Stiffness factor
It is ratio of moment of inertia to the length of the beam is called stiffness factor of beam.
Moment required to rotate an end by a unit angel when rotation is permitted at that end is called stiffness of the beam
Stiffness of the beam AB=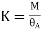
Types of far end support | K |
| I/L |
2. If far end is simply supported Roller support, Internal hinged and overhang | 3I/4L |
Carry over factor:
It is defined as the ratio of moment developed at far or adjacent end of the moment applied at the near end.
The ratio of carryover moment to applied moment is called carry-over factor.
Carryover factor=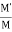
Types of toes and support
Fixed support ½
Intermediate support ½
Rigid joint ½
Roller hinged, internal 0
Overhanging 0
If for the end is fixed 1/l
If for the end is simply roller internal hinged, I overhung 3I/4L
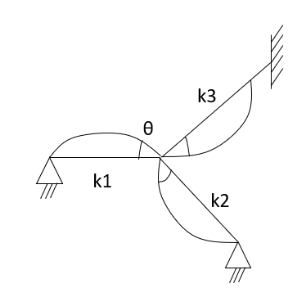
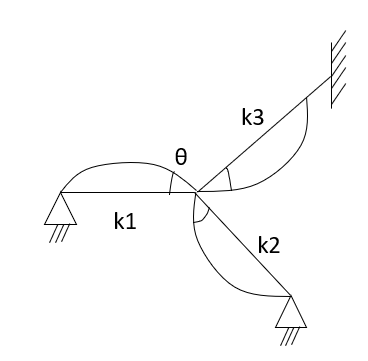
Distribution factor
It is ratio of the stiffness of member to the total stiffness of the joint where all the members are meeting.
A moment which tends to rotate without translation a joint to which several members are connected will be divided amongst connected member in proportion to their stiffness.
Distribution factor (DF) 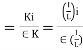
Thus, distribution factor is the ratio of the stiffness of member to the total stiffness of the joint where all members are meet.

Examples: To find stiffness
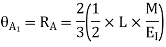
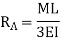

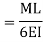
Then consider at the B end

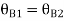
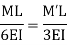
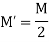
Carryover factor = 

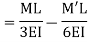
Put 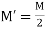

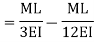
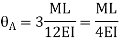
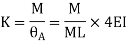
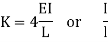
Distribution factor =>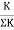
Q2) Write down application of MD method to continuous beam with fixed ends?
A2) Application of MD method to continuous beam with fixed ends: -
Q3) Write down producer of analysis of moment distribution method?
A3) Steps for analysis of moment distribution method
Distribution factor is=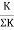
K=stiffness -it depends on the support condition.
1. Far end fixed &intermediate support =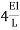
2. The far end simply supports = 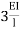
COF - support
O - Simply support
½ - fixed
½ - intermediate
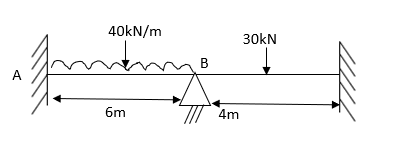
Q4) Analyze the given beam by M.D. method (10 marks item)
AB=>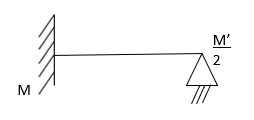
A4) Step 1) Fixed end moment
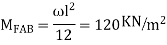
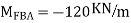
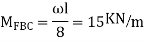
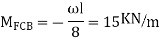
Step 2) Distribution factor
Draw distribution table
1) Draw distribution table
Joint | Member | K |
|
|
B | BA
BC |
|
| 0.4
0.6 |
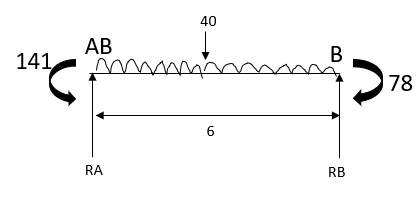
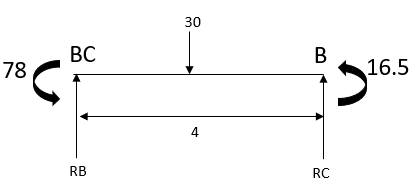
2) Moment distribution Table
0.4 | 0.6 | |||
Member | AB BA | BC CD | ||
Fixed end
balancing | 120 - 120
42 | 15 -15
63 | ||
COF
Balancing | 21 0 0 | 31.5 | ||
Final moments
| 141 -78 | 78 16.5 | ||
|
|
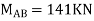
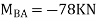
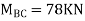






Step 4) Draw SFD and BMD
SFD
BMD

Q5) Analyze the given beam ABCD by moment distribution method?
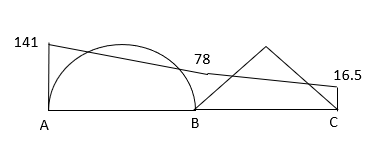
A5) Step 1) Find fixed moment
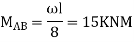
 KNM
KNM
 KNM
KNM
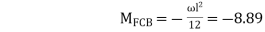 KNM
KNM
 KNM
KNM
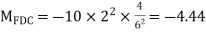 KNM
KNM
Step 2) Distribution factor
JOINT | MEMBER | K |
|
|
B | BA
BC
|
|
5EI | 0.2
0.8 |
C | CB
CD |
|
4.5EI | 0.89
0.11 |
3)Moment Distribution Table
0.2 | 0.8 |
| 0.89 | 0.11 | ||||
Members | AB BA 15 -15
| BC CB 13.33 -13.33
| CD DC 8.89 -4.44
2.22 + 4.44 | |||||
Fixed End | ||||||||
Balancing | ||||||||
Initial Moments
Balancing | 15 -15
0.331 | 13.33 -13.33
1.34 1.98 | 11.1 0
0.25 | |||||
COF
Balancing | 0.165
-0.19
| 0.99 0.67
-0.79 -0.59 |
-0.07 | |||||
COF
Balancing | -0.09
0.058 | -0.29 -0.39
0.22 0.34 |
0.04 | |||||
Final Moments | 15.075 -14.801
| 14.8 -11.32 | 11.32 0 | |||||
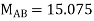 KNM
KNM
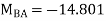 KNM
KNM
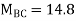 KNM
KNM
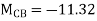 KNM
KNM
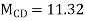 KNM
KNM
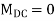 KNM
KNM
Step 4) Draw BMD
BMD
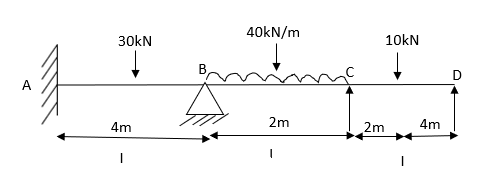
Q6) Analyze the given beam by M.D. method

A6) Step 1) Find fixed end moment

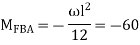
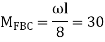
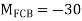
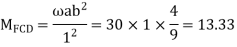

Step 2) Distribution Factor
Joint | Members | K |
|
|
B | BA
BC |
|
2.5 EI | 0.2
0.8 |
C | CB
CD |
|
| 0.66
0.33 |
Moment distribution table
0.2 | 0.8 |
| 0.66 | 0.33 | ||||
Members | AB BA | BC CB | CD DC | |||||
Fixed End | 60 -60
-60 -30
| 30 -30
| 13.33 -6.66
3.33 +6.66
| |||||
Balancing | ||||||||
Initial Moments
Balancing | 0 - 90
12 | 30 -30
48 8.8 | 16.66 0
4.40 | |||||
COF
Balancing |
-0.88 | 4.4 24
-3.52 -15.84 |
-1.92 | |||||
COF
Balancing |
1.58 | -7.92 -1.76
6.33 1.16 |
0.58 | |||||
COF
Balancing |
- 0.11 | 0.58 3.16
-0.46 -2.08 |
-1.04 | |||||
COF
Balancing |
0.20 | -1.04 -0.23
0.83 0.15 |
0.07 | |||||
Final Moments | 0 -77.21 | 77.21 -12.64 | 12.75 0 | |||||
Step 4) Draw BMD
BMD
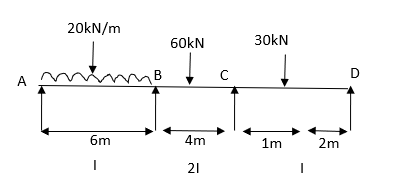
Q7) Analyze the given frame by MD method
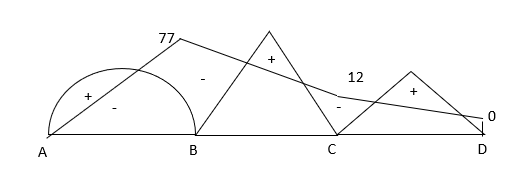
A7) Step 1) Find Fixed End Moments
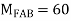
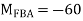
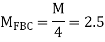
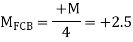
Step 2) Distribution Factor
Distribution table
joint | Member | K |
|
|
B | BA |
| 1.41 | 0.47 |
| BC |
| 1.41 | 0.53 |
Step 3) Moment Distribution Table
0.47 | 0.53 | |||
Member | AB BA | BC CB | ||
External moment
Fixed end
Balancing |
60 - 60
| 135
2.5 -2.5
-1.25 2.5 | ||
Initial Moment
Balancing | 60 -60
27.61 | 1.25 135
31.13 | ||
COF
Balancing | 13.8 0
0 | 0
0 | ||
Final moments
| 73.8 -32.39 | 32.39135 | ||
BMD

Q8) Analyze the given beam ABCD having pt B is sink by 10mm EI 
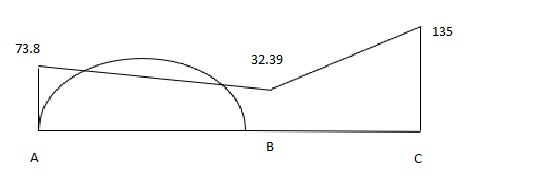
A8) For AB Span 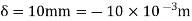
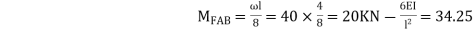 KNM
KNM
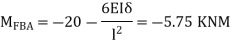
BC= +VE
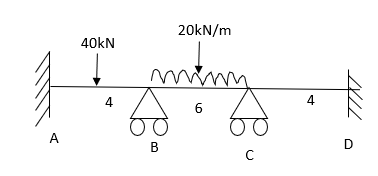
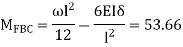
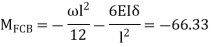
CD=0  No loading
No loading

Step 2) Distribution factors
Joint | Members | K |
|
|
B | BA
BC |
|
1.66 | 0.60
0.40 |
C | CB
CD |
|
| 0.40
0.60 |
Step 3) Moment Distribution Table
0.6 | 0.4 |
| 0.4 | 0.6 | ||||||||
Members | AB | BA | BC | CB | CD | DC | ||||||
Fixed end
Balance | 34.25
| -5.75
-28.74
| 53.66
-19.16 | -66.33
26.53 | 0
39.79 | 0
| ||||||
COF Balancing | +14.37 | -7.95 | 13.26 -5.30 | -9.58 +3.83 |
+5.74 | 19.89 | ||||||
COF Balancing | -3.97 |
-1.14 | 1.91 -0.76 | -2.65 1.06 |
1.59 |
| ||||||
COF
Balancing | -0.57 |
-0.31 | 0.53
-0.21 | 0.38
0.15 |
0.22 | 0.79 | ||||||
Final Moments | 15.34
| -43.89 | 43.89 | -46.61 | -46.61 | 20.68 | ||||||
Q9) Draw BMD by Moment Distribution Method and C support is sink by 25mm
A9) For AB 
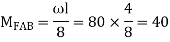
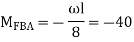
For BC  mm
mm
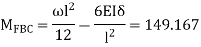
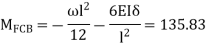
For CD  mm
mm
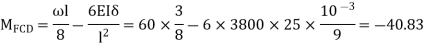
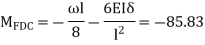
Step 2) Distribution factor
Joint | Members | K |
|
|
B | BA
BC |
|
| 0.33
0.66 |
C | CB
CD |
|
| 0.66
0.33 |
Step 3) Moment Distribution Table
0.33 | 0.66 |
| 0.66 | 0.33 | ||||||||
Members | AB | BA | BC | CB | CD | DC | ||||||
Fixed end | 40 | -40 | 149.16 | 135.83 | -40.83 42.91 | -85.83 +85.83 | ||||||
Final Balance | 40 | -40 -36.02 | 149.16 -72.04 | 135.83 -91.02 | 2.08 -45.51 | 0
| ||||||
COF Balancing | -18.01 |
15.02 | -45.51 30.04 | -36.02 23.77 |
11.89 |
| ||||||
COF Balancing | 7.505 |
-3.92 | 11.89 -7.85 | 15.02 -9.91 |
-4.957 |
| ||||||
COF
Balancing | -1.96 |
1.64 | -4.96
3.28 | -3.93
2.59 |
1.296 |
| ||||||
Final Moments | 29.28 | -63.28 | 64.01 | 36.33 | -35.20 | 0 | ||||||
Q10) Analyze the frame shown in fig. by MDM and Draw BMD
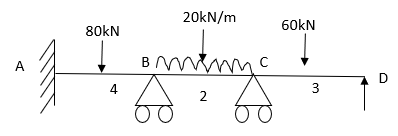
A10) Step 1) Fixed End Moments
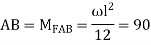
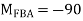
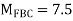
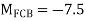
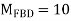

Step 2) Distribution Factor
Joint | Members | K |
|
|
B | BA
BD
BC |
|
2.33 | 0.28
0.43
0.28 |
Step 3) Moment Distribution Table
0.28 | 0.43 | 0.28 | ||||||
Members | AB | BA | BD | BC | CB | DB | ||
Fixed end
Balance | 90
| -90
20.3
| 10
31.17 | 7.5
20.3 | -1.5 | -10
| ||
Cot Balancing | 10.15 | 0 0 | 0 0 | 0 0 |
10.15 | 15.58 | ||
Final |
100.15 |
-69.7 |
42.17
|
27.8 |
2.65 |
5.58 | ||
Step 4) Draw BMD and SFD
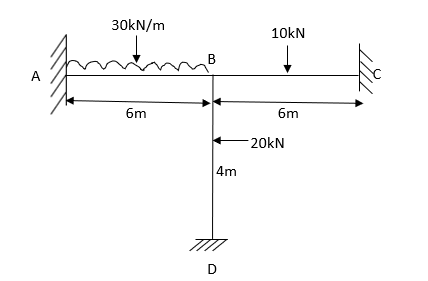
BMD
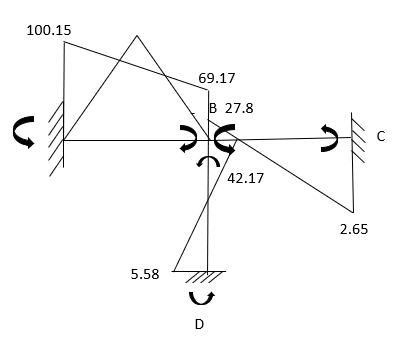
Q11) Determine Moments of the given figure by moment Distribution Method
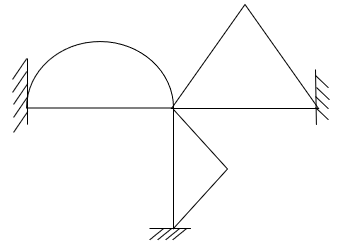
A11) Step 1) Non-sway
Step 2) Fixed End moments
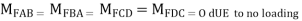
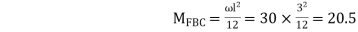 knm
knm
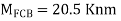
Step 3) Distribution factor
Joint | Members | K |
|
|
B | BA
BC |
|
| 0.43
0.57 |
C | CB
CD |
|
| 0.64
0.36 |
Step 4) Moment Distribution table
0.43 | 0.57 |
| 0.64 | 0.36 | |||||||
Members | AB | BA | BC | CB | CD | DC | |||||
Fixed end | 0 | 0 | 22.5 | -22.5 | 0
| 0 | |||||
Initial Balance | 0 | 0 -0.96 | 22.5 -1.28 | -22.5 +1.14 | 0 +0.81 | 0
| |||||
COF Balancing | -0.48 |
0.24 | +0.57 0.32 | -0.64 0.40 |
0.23 |
| |||||
COF Balancing | 0.12 |
-0.086 | 0.20 -0.114 | 0.16 -0.10 |
-0.057 |
| |||||
Final Moments | -0.36 | -0.806 | 0.806 | -3.57 | -0.637 | 0 | |||||
Q12) Analyses the given frame as shown. By MDM
A12) Step 1) Fixed end moment
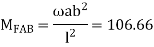

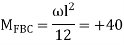
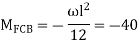
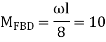
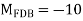
Step 2) Distribution Factor
Joint | Members | K |
|
|
B | BA
BD
BC |
|
3.455 EI | 0.40
0.28
0.32 |
Moment Distribution Table
0.40 | 0.28 | 0.32 | |||||||
Members | AB | BA | BD | BC | CB | DB | |||
Fixed end | 106.66 | -53.33 | 10 5 | 40 20 | -40 40
| -10 +10 | |||
Initial Balance | 106.66 | -53.33 -8.66 | 15 -6.06 | 60 -6.43 | 0
| 0
| |||
COF Balancing | -4.33 | 0 0 | 0 0 | 0 0 |
|
| |||
Final Moments |
102.35
| -61.99 |
8.94 |
53.07
|
0 |
0 | |||
Step 5) Draw BMD

Q13) Analyze the non-sway frame as shown in fig. by MDM
A13) Step 1) Fixed end moment
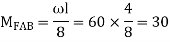

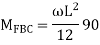

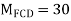
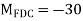
Step 2) Distribution factor
Joint | Members | K |
|
|
B | BA
BC |
|
| 0.70
0.30 |
C | CB
CD |
|
| 0.30
0.70 |
Step 4) Moment Distribution table
0,70 | 0.30 |
| 0.30 | 0.70 | |||||||
Members | AB | BA | BC | CB | CD | DC | |||||
Fixed end | 30
-30 | -30
-15 | 90 | -90 | 30
15 | -30
30 | |||||
Initial
Balance | 0 | -45
-31.5 | 90
-13.5 | -90
13.5 | 45
31.5 | 0 | |||||
COF Balancing |
|
-4.72 | 6.75 -2.02 | -6.75 2.02 |
4.72 |
| |||||
COF Balancing |
|
-0.7 | 1.01 -0.3 | -1.01 0.3 |
0.7 |
| |||||
COF Balancing |
|
-0.1 | 0.15 -0.04 | -0.15 0.04 |
0.1 |
| |||||
Final Moments
|
0 |
-82.2 |
82.2 |
82.2 |
-82.2 |
0 | |||||
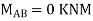

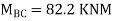

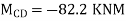
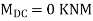
Step 4) Draw BMD
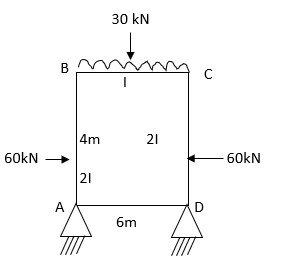
Q14) Analyze the given frame by moment distribution method take EI Constant
A14) Step 1) Find Distribution Factor
|
|
|
|
| ||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||
Step 2) Non sway moment distribution moment Table
Members | AB BA | BC CB | CD DC |
Fixed End Balancing | 0 0 0 | 0 0 0 0 | 0 0 0 |
Final Moments | 0 0 | 0 0 | 0 0 |
Step 3) Assumption For sway Frame


Step 4: Horizontal thrust at A 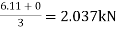
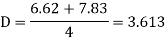
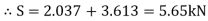
Actual Sway force of 12 kN
 Draw Sway Moment Distribution Table
Draw Sway Moment Distribution Table
0.33 | 0.67 |
| 0.67 | 0.33 | ||||||
Member | AB | BA
| BC CB
| CD DC | ||||||
FEM Balancing | 0 | 8 | 0 | 0 | 9 | 9 | ||||
| -2.67 | -5.33 | -6.00 | -3.00 |
| |||||
| COF Balancing |
|
1 | -3 | -2.67 |
| 1.5 | |||
| 2 | 1.78 | 0.85 |
| ||||||
| COF Balancing |
|
-0.30 | 0.69 | 1 |
|
| |||
| -0.39 | -0.67 | -0.33 |
| ||||||
| COF Balancing |
|
0.11 | -0.33 | -0.30 |
| 0.17 | |||
| 0.22 | 0.20 | 0.10 |
| ||||||
| COF Balancing |
|
-0.03 | 0.10 | 0.11 |
| 0.05 | |||
| -0.07 | -0.07 | 0.05 |
| ||||||
| 0 | 6.11 | -6.11 | -6.62 | 6.62 | 7.83 | ||||
| ||||||||||
Step 6) Final Moments Table:
Member | AB BA | BC CB | CD DC | ||||
Non-Sway Moment | 0 0 | 0 0 | 0 0 | ||||
Sway Moment | 0 | 6.11 | -6.11 | -6.62 | 6.62 | 7.83 | |
Actual Sway | 0 | +12.98 | -12.98 | -14.06 | +14.06 | +16.6 | |
Final Moment (Addition of Non-Sway Moment +corrected moment by sway) | 0 | +12.98 | -12.98 | -14.06 | +14.06 | +16.6 | |
 Correct Horizontal A reaction
Correct Horizontal A reaction 
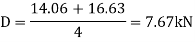
Q15) A two hinged portal frame ABCD consist of a vertical columns AB, DC at 4m height if the beam BC of 3m the frame carried a vertical point load of 120kN on the beam at a distance of 1m from B find the reaction at support.
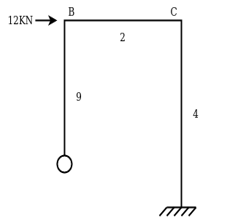
A15)
Non-Sway analysis:
Step 1) Fixed end moment
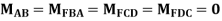
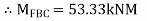
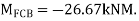
Step 2) Draw Distribution Factor Table
Joint | Member | K | ƩK | D.F. |
B | BA | 3EI/L= 3EI/4 = 0.75 EI |
2.08 EI | 0.36 |
BC | 4EI/L= 4EI/3=1.33 EI | 0.64 | ||
C | CB | 4EI/L = 4EI/3=1.33EI |
2.08 EI | 0.64 |
CD | 3EI/L= 3EI/4=0.75 EI | 0.36 |
Step 3) Draw Non sway moment distribution Table
0.36 | 0.64 |
| 0.64 | 0.36 | ||||
Member | AB BA | BC CB |
| CD DC | ||||
FEM Balancing | 0 -19.2 | 53.33 -26.66 -34.13 17.06 |
| 0 0 9.6 | ||||
COF Balancing |
-3.07 | 8.53 -17.07 -5.46 10.92 |
|
6.15 | ||||
COF Balancing |
-1.96 | 5.46 -2.73 -3.49 1.75 |
|
0.98 | ||||
Final Moments | 0 -24.23 | 24.24 -16.73 |
| 16.73 0 | ||||
Horizontal reaction 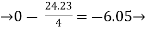
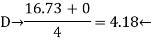
 Sway force = 1.87 kN
Sway force = 1.87 kN 
Sway analysis
Step 4) Initial equivalent moments are negative.
 :
: 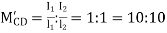
0.36 | 0.64 |
| 0.64 | 0.36 | ||||
Member | AB BA | BC CB |
| CD DC | ||||
FEM Balancing | 0 -10 3.6 | 0 0 6.4 6.4 |
| -10 0 3.6 | ||||
COF Balancing |
- 1.15 | 3.2 3.2 -2.05 -2.05. |
|
-2.05 | ||||
COF Balancing |
0.35 | - 1.03 -1.03 0.66 0.66 |
|
0.35 | ||||
Final Moments | 0 -7.2 | 7.2 7.2 |
| -7.2 0 | ||||
Horizontal reaction 

Resolving force horizontally = 1.81 +1.81 =3.63kN
Actual Sway = 3
Sway 0 7.27 | 7.27 7.27 | -7.27 0 |
| +3.64 3.64 | -3.64 0 |
Non-Sway 0 21.17 | -21.17 21.17 | -21.17 0 |

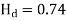
Q16) Analyses the rigid frame shown in fig by M.D. method.
A16) Step1) Fixed end moment
Fixed end moment in all the members = 0
Step 2) D.F
B | BA |
|
| 2.33EI | 0.57 |
BC |
|
| 0.43 | ||
C | CB |
|
| 2.5EI | 0.4 |
CD |
|
| 0.6 |
Conclude S = 80 kN
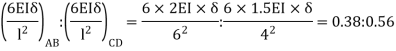
Sway Force
Consider FBD for column
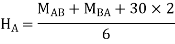
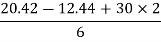
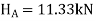

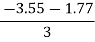
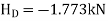
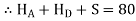
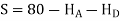
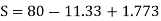
SWAY ANALYSIS
Consider Sway on right hand side
 is
is 
 is
is 
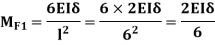
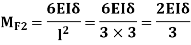
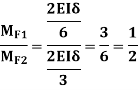
Consider 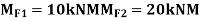
Moment distribution maybe carried out.
A B C D
10 | 0.5 10 | 0.5
| 0.5
| 0.5 20 |
20 |
| -5 | -5 | -10 | -10 |
|
-2.5
|
2.5 | -5 | -2.5 |
| -5 |
2.5 | 1.25 | 1.25 |
| ||
1.25
|
-0.32 | 0.63 | 1.25 |
| 0.63 |
-0.32 | -0.62 | -0.62 |
| ||
-0.16
|
+0.16 | -0.31 | -0.16 |
| -0.31 |
0.16 | 0.08 | 0.08 |
| ||
0.08
|
-0.02 | 0.04 | 0.08 |
| 0.04 |
-0.02 | -0.04 | 0.04 |
| ||
+8.67 | -7.32 | -7.32 | -10.66 | 10.66 | 15.35 |

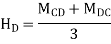
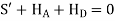
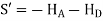
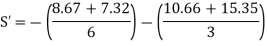
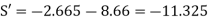
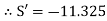
Sway Correction Factor 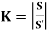
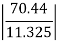
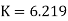
|
|
|
|
|
|
|