Unit - 4
Curves
Q1) Explain Horizontal and Vertical curve?
A1) Horizontal curve:
Vertical Curve:
Q2) Explain about Simple curve?
A2)
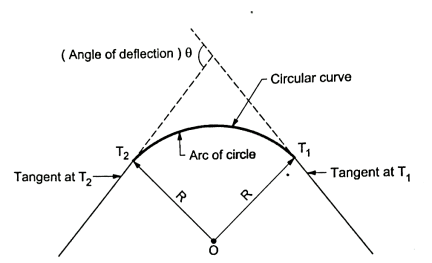
Fig.: Simple curve
Q3) Explain about Compound curve?
A3)
for better understanding.
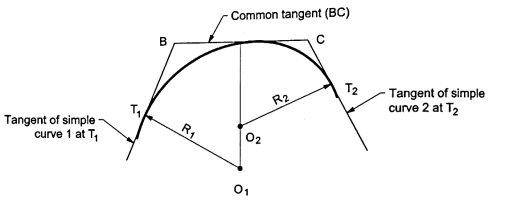
Fig.: Compound curve
Q4) What are the advantage and disadvantage of reverse curve?
A4) Advantages of reverse curve:
Disadvantages of reverse curve:
Q5) What are the types of vertical curve?
A5) There are Two types of vertical curve:
Summit curves:
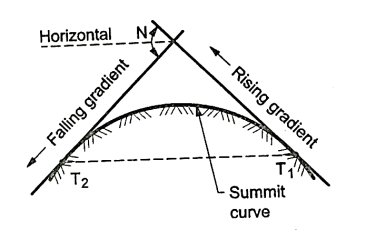
Fig.: A rising gradient intersecting a falling gradient
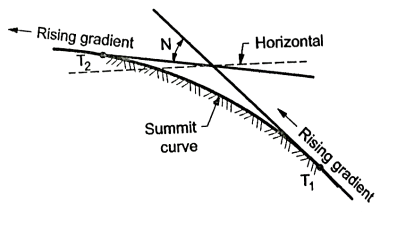
Fig.: A rising gradient meeting another rising gradient
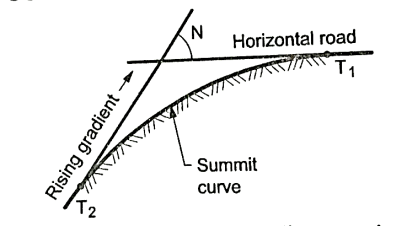
Fig.: A rising gradient meeting at horizontal road
Valley curves:
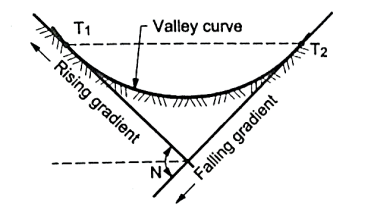
Fig.: A falling gradient intersecting a rising gradient
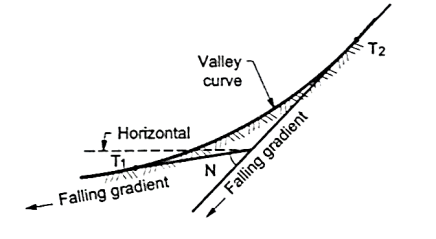
Fig.: A falling gradient meeting another falling gradient
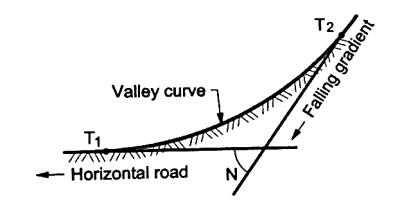
Fig.: A falling gradient meeting a horizontal road
Q6) Explain about simple circular curve?
A6)
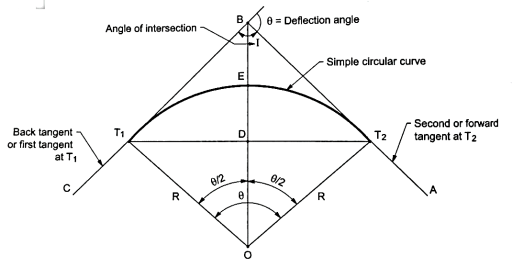
Fig.: Simple circular curve (Right hand curve)
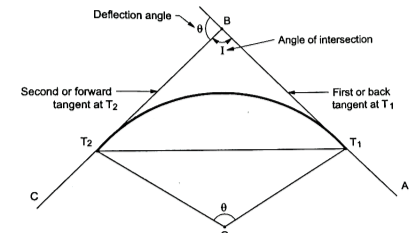
Fig.: Simple circular curve (left hand curve)
4. In Fig., the curve deflects to left side. Therefore, it is called as left-hand curve.
5. In Fig., BC is first tangent and also called as back tangent. AB is second tangent and also called as forward tangent. In Fig.AB is first or back tangent at T₁ and BC is second or forward tangent at T₁.
6. T1, and T2, are the tangent points. T1, shows the starting of the curve and T2, shows the end of the curve.
7. In fig., I is an angle of intersection and 0 is a deflection angle.
8. BT1, and B T2, are the lengths of tangent.
9. T1, T2, is a long chord of length 'L'.
10. The arc 'T1ET2' is a length of curve.
11. The mid point 'E' is apex of summit of the curve T1ET2
12. BE is the distance of apex.
13. The angle 'T1OT2' = The deflection angle ' '.
'.
14. DE is a versed sine of the curves.
Q7) Explain about Compound curve?
A7)
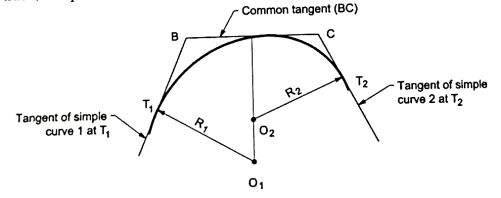
Fig.: Compound curve

Fig.: Two centered compound curve
Let,
Rs =the smaller radius (T1O1)
R2= the longer radius (T2O2)
BC= common tangent
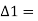 deflection angle between the rear and the common tangent.
deflection angle between the rear and the common tangent.
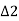 =deflection angle between the common and the forward tangent.
=deflection angle between the common and the forward tangent.
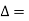 total deflection angle.
total deflection angle.
ts=the length of the tangent to the arc (T, D) having a smaller radius.
Ts = tangent distance T1A corresponding to the shorter radius.
TL = tangent distance T2A corresponding to the longer radius.
From Fig. we have,
ts= T1B= BD= Rs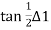
tl=T2C=CD+RL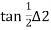
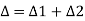
From triangle ABC we have,
Ts=T1B+BA
=ts+(ts+tl)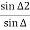
Q8) Explain setting out by radial offsets?
A8)
T1P = x
From Δ T1 PO,
PO2 = T1O2+T1 P²
Ox=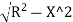 –R …. (1)
–R …. (1)
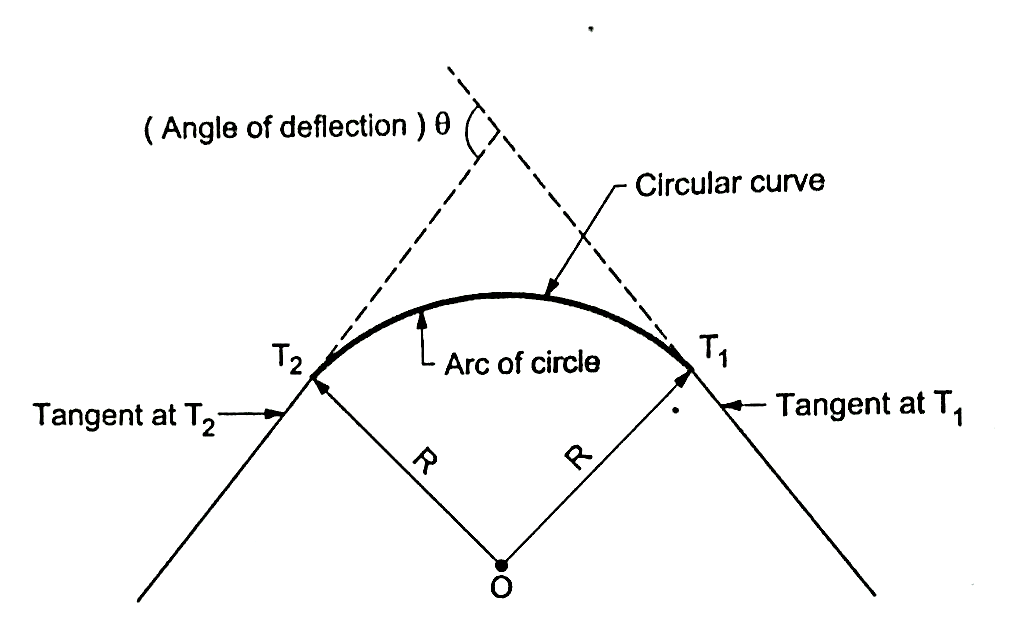
Fig.: setting out by radial offsets
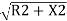
Thus,
Ox=R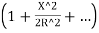 -R
-R
Neglecting the other terms except the first two, we get
Or Ox=x2/ 2R
When the radius is large
T1P2=PN(2R+PN)
X2=Ox(2R+Ox)
Neglecting Ox in comparison to 2R we get
Ox=x2/2R
Q9) Explain setting out by perpendicular offset?
A9)
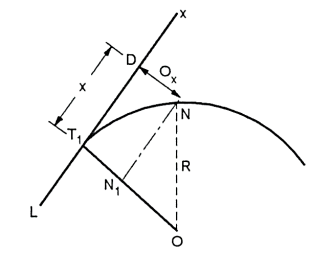
Fig.: setting out by perpendicular offsets
Let DN=Ox= offset perpendicular to the tangent
T1D=x= measured along the tangent
Draw NN1 parallel to the tangent
From 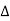 leEE1O, we have
leEE1O, we have
E1O2=EO2-E1E2
(R-Ox)2=R2-x2
From which
Ox=R-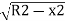
The corresponding approximate expression for Ox may be obtained by expanding the term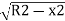 . Thus,
. Thus,
Ox=R-R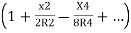
Neglecting the other terms except the first two of the expressions
Ox=R-R+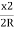
Q10) Explain Successive bisection of chords?
A10)
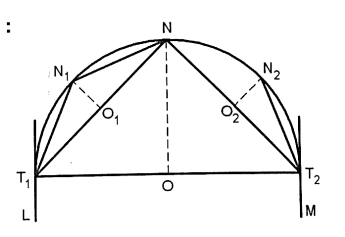
Fig.: Successive bisection of arcs
NO= R (1-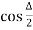 )
)
=R- ^2
^2
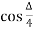
Q11) Explain two theodolite method of deflection angle?
A11)
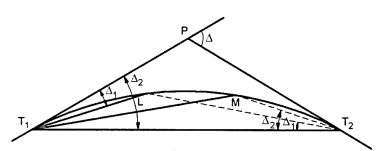
Fig.: Two theodolite method
Thus, in Fig.
<PT1L= A=Deflection angle for L.
But LT2T1, is the angle subtended by the chord T, L in the opposite segment.
∴ angle LT2T1= angle PT1M =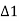
Similarly, angle PT1L=  = angle T1T2M
= angle T1T2M
Hence the angle between the long chord and the line joining any point to T2 is equal to the deflection angle to the point measured with respect to the rear tangent.
Method of setting out the Curve:
Q12) Explain advantages and disadvantages of two theodolite method?
A12) Advantage of two theodolite method:
Disadvantage of two theodolite method:
Q13) Explain Transition curve?
A13)
Necessity: