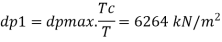Unit - 3
Unsteady Flow
Q1) Explain Introduction to flow through sharp crested circular orifice under constant head?
A1)
Unsteady flow is defined as the flow in which the characteristics of flow like velocity, pressure at a point called respect to time.
For unsteady flow 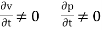
Example of unsteady flow are
(1) Liquid falling under gravity from the opening in the bottom of container.
(2) Liquid flow in the suction and pressure pipes of a reciprocating pump.
(3) Wave motion and cyclic movement of large bodies of water in tidal flow
(4) Flow through open channel when discharge or depth or both vary.
Development of flow in a pipe
- When the valve is closed the velocity of flow is zero.
-When the valve is opened at time t, the fluid flow with certain velocity and velocity is changes.
-From time t1, to t2, the flow is called as unsteady flow.
-After time t, the flow stable fully and assumes a steady flow.
Q2) What is Types of unsteady flow?
A2)
The unsteady flow is classified on the basis of variation of variable.
(a) Flow in which variation of variables is rapid and random. e.g. Turbulent flow.
(b) Flow in which the variations of velocity are periodic, either slow or rapid. e.g. Flow subjected to force i.e. surge tank, water hammer etc.
(c) Flow in which flow is caused due to motion of body at constant velocity. e.g. Flow due to translation of surges and waves.
(d) Flow in which the variation is non-periodic and slow. e.g. Flow through opening under varying head, flow routing etc.
Q3) What is Flow through openings under varying head?
A3)
Consider a tank being emptied with a device.
Let H, be the head on the device initially and it is required to find the time 't' required to reduce the head up to 'H₂' above the device.
Let 'h' be the head on the device at any instant and let it fall by 'dh' in short interval of time 'dt'.
If A is the area of liquid surface in plan when the head acting is 'h', Volume of liquid leaving the tank in time 'dt' = A.dh
The discharge through the device under head 'h' in time dt = Q dt Where 'Q' is the discharge passing through the device under head 'h'.
Volume of liquid leaving the tank = Discharge through the device in time
-A. Dh = Q dt
[Note: As time increases, the head on the device decreases and hence the negative sign]
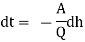
Integrating the equation, we can write
Time of emptying tank,
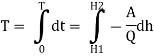
Two cases arise: -
i) A-constant: Express 'Q' in terms of 'h' and integrate.
Ii) A-variable: Express both A and Q in terms of 'h' and integrates
Time of Emptying a Hemispherical Tank
A hemispherical tank of the radius R and having an orifice of area at a the bottom is represented by diagram mentioned under.
Consider the head of water over the orifice fall from a value H, to a value H, in t seconds time.
Let 'h' be the head of water over the orifice and the radius of water surface at this level is 'x' Obviously,
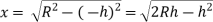
Area of water surface
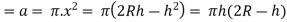
Suppose water level falls in dt seconds by dh
Therefore, amount of water fallen in dt seconds
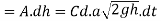
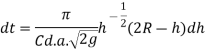
Thus, time required to change the head of water from H, to H, is obtained the above quantity from the limits of h
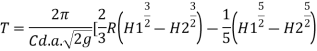
If the tank is emptied,
Then H, R and H₂-0
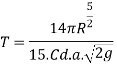
Time of Emptying a Cylindrical Tank through an Orifice at its bottom
The configuration of the system is shown in Fig.
The radius of the tank is R and its length is L, the initial and final heights of the liquid in the tank are h, and h, as shown in Fig. a is the area of orifice. We have to find the time t when the level in the tank falls from h to by
At some instant, the height of the liquid in the tank is h.
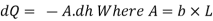
In a time dt, the level in the tank falls through dh then, the liquid going out from the tank
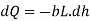
Where b is the width of liquid in the tank which is changing with respect to time
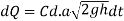
The amount of liquid going out of orifice during the time di is given by.
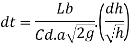
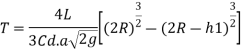
Q4) What is Fluid compressibility?
A4)
It is the measure of elasticity in fluid.
Fluids are compressed under pressure due to change in their mass density.
More mass can be accommodated in the unit volume and when the pressure is removed the fluids regain to its original volume.
As the pressure is increased, the volume is decreased
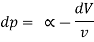
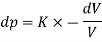
Where K is the constant of proportionality is known as bulk modulus.
- If K is more, is less indicating less volume change i.e. less compressibility. That is why compressibility expressed as inverse of bulk modulus
Higher the bulk modulus less is the compressibility of fluid.
Fluids are compressed under pressure due to change in their mass density
Liquids are generally considered to be incompressible. For instance, a pressure of 113078 kPa will cause a gives volume of water to decrease by only 5% from its volume at atmospheric pressure.
Gases on the other hand, are very compressible. The volume of a gas can be readily changed by exerting an external pressure on the gas.
Water hammer and cavitations are the example of the importance of compressibility effects in liquid flows Compressibility effects are very important in the design of modern high-speed aircraft, missiles, power plants, fans and compressors
Bulk Modulus
It is the ratio of compressive stress to volumetric strain. It is denoted by "K"
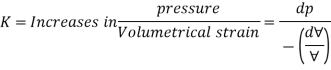
Dp = Increase in pressure Volumetric strain dp
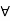 = Volume of gas enclosed in cylinder,
= Volume of gas enclosed in cylinder,
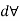 =Change in volume
=Change in volume
Negative sign indicate decrease in volume with an increase in pressure.
Value of K Water is 2.05 x 10^9' N/m². Air is 1.02 x 10^5' N/m²
We know,
Density
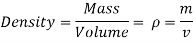
Since the mass m of a certain volume V is constant, differentiate Equation
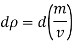
But Bulk modulus
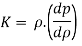
Q5) Explain Celerity of elastic pressure wave through fluid medium?
A5)
When the pipe is plastic the effect of pipe elasticity on the celerity of pressure wave is to be considered.
Elasticity effect for both pipe and fluid is to be considered. Effective bulk modulus of elasticity of fluid is considered both compressibility of fluid and elasticity of pipe. It is denoted by K
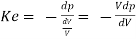
Total change in volume = (change in volume due compression of fluid) + (change in volume due expansion of pipe wall)
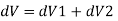
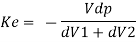
Taking reciprocal, we get
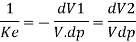
When the pipe is elastic, the effect of pipe elasticity on the celerity of pressure wave is to be com
Increment in circumferential stress df
Resisting force = bursting force
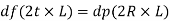
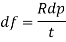
Circumferential strain= Stretched in pipe circumference/ origin circumference
Bulk modulus of elasticity of pipe material
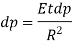
Changes in volume
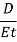
Celerity of pressure wave through elastic medium through an elastic pipe
Q6) What is Water hammer phenomenon?
A6)
When the water is flowing through a pipe it possesses some momentum. This momentum is destroyed, if the flow water is suddenly brought to rest by closing the valve.
The sudden change in momentum will cause a sudden rise in pressure.
The high pressure wave is transmitted along the pipe forward and backward
The sudden rise in pressure has the effect of hammering action on the wall of the pipe is known as water hammer. If the hammer blow is very high, the pipe can burst.
To avoid the pipe bursting, the valve of pipeline or penstocks is to be closed gradually.
Principle Components of Turbo Machines
Q7) Explain Rise of pressure due to water hammer?
A7)
The pressure rise due to water hammer depends upon:
- Velocity of flow
- Length of pipe
- Time taken to close the valve
- Elastic properties of material
Following cases of water hammer in pipe depending upon the time taken in closing the value.
1. Gradually closure of valve
2. Suddenly closure of valve
- Gradually Closure of Valve
Consider a pipe line of uniform cross-section through which water is flowing, whose valve is gradually closed Let,
L= length of pipe,
A = cross-sectional area of pipe
V = velocity of flow, time in second required to close the valve.
p = intensity of pressure wave produced
Mass of water in pipe= weight density x volume = p AL
Rate of retardation of water = 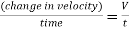
Force = mass x acceleration
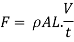
Pressure = Force /Area
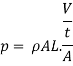
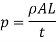
Pressure head due to increase in pressure
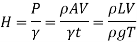
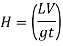
Valve head due to increase in pressure
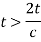
Where t= time in second
C= velocity of pressure wave
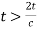 = then the valve closure is considered to be sudden
= then the valve closure is considered to be sudden
2. Suddenly Closure of Valve in a Rigid Pipe
Increase in pressure due to gradually closure of valve is
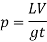
If the valve fitted to a pipeline is suddenly or instantaneously closed (t= 0), the increase in pressure will be infinite. In actual practice, it is not possible to close the valve instantaneously. It has been derived on assumption that liquid flowing through the pipe is incompressible
Consider a pipe of uniform cross-section through which water is flowing with uniform velocity whose valve is suddenly closed
Let,
A= cross-sectional area of pipe.
L = length of pipe
V = velocity of flow
K= bulk modulus of water
P = intensity of pressure wave produced
Loss of kinetic energy = ½ mass x velocity^2
The strain-energy stored in water volume
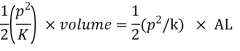
Equating loss of energy to strain energy stored in the water.
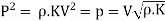
3. Suddenly closure of valve in elastic pipe
Consider a pipe of uniform cross-section through which water is flowing whose valve is suddenly closed. Assume the pipeline is perfectly elastic
Let
L = length of pipeline.
D = diameter of the pipe
t= thickness of pipe wall
E= modulus of elasticity of pipe materials.
When the valve is closed suddenly and pipe possess elasticity, the circumferential and longitudinal stresses induced in the pipe wall
Circumferential stress
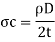
Longitudinal stress
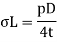
Volume of pipe wall
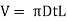
Where, p increase in pressure due to water hammer
Strain energy stored in the pipe walls per unit volume
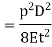
Total strain energy stored in pipe material
= strain energy per unit volume x volume
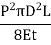
Loss of kinetic energy of water
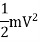
Gain of strain energy in water
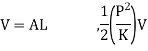
Now, (loss of kinetic energy of water energy) = (Gain of strain energy in water) + (Gain of strain energy in water)
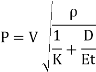
Q8) What is Surge tanks and its function?
A8)
A surge tank is a tank fitted to a pipeline in the upstream side of the control valve which is used to control and stop the flow of water through the pipe.
It is provided on the penstock in a hydropower generation plant. The surge tanks are placed as close to the turbine as possible.
The height of surge tank is generally kept above the maximum water level in the supply level reservoir.
Types of surge tank
- Simple surge tank
- Differential surge tank.
- Restricted orifice type surge tank
Function of Surge Tank
- It is used to control the pressure variation due to rapid changes in pipeline flow, which reduces ill-effect of water hammer.
- It is also to supply additional water if needed for more power generation
Q9) The water is flowing with a velocity of 1.5 m/s in a pipe of length 2500 m and of diameter 500 mm. At the end of the pipe, a valve is provided. Find the rise in pressure if the valve is closed in 25 seconds. Take the value of C = 1460 m/s. What will be rise in pressure if the valve is closed in 2 second.
A9)
Given:
Velocity of water,
V = 1.5 m/s
Length of pipe,
L = 2500 m
Diameter of pipe,
D = 500 mm = 0.5 m
Case I: Time to close the valve
t = 25 seconds
Value of C = 1460 m/s
Let the rise in pressure p
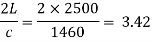
We know if t>, the closure of valve is said to be C gradual.
t = 25 sec and 2L/c= 3.42
t>valve is closed gradually.
For gradually closure of valve, the rise in pressure as,
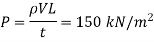
Case II: Valve is closed in 2 second, Since t<3.42, the valve is closed rapidly.
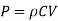
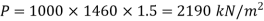
Q10) Water is flowing through a pipe of diameter 40 cm and length 2400 m with a velocity of 2.5 m/s. A valve is provided at the end of the pipe. If the valve is closed in 30 seconds find the rise in pressure. Take the velocity of pressure wave as 1500 m/s
A10)
Pipe diameter
D = 40 cm = 0.4 m,
Length of pipe, L= 2400 m Velocity of water, V = 2.5 m/s,
Time to close the valve,
t = 30 sec.
Velocity of pressure wave, c = 1500 m/s
To find: Rise in pressure 'p'
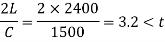
If t>2L/c, the closure of valve is said to be gradual.
2.5>3.2, hence the valve is closed gradually. The rise in pressure for gradually closure of valve is given by,
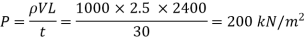
Q11) Find the rise of pressure in pipe line carrying water when the valve at the end of pipe is closed suddenly at 1.5 seconds. Take the dimensions of pipe as, diameter 25 cm, length - 1250 m, velocity of flow= 1.5 m/s. D=0.25 m
A11)
Given: V=1.5 m/s, L=1250 m, T=1.5 sec,
Assume K= 19.62 x 10' N/m²
Critical time
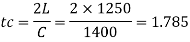
Since the closer time is less than critical time. T<t, then the closure is sudden.
T<tc then the closure is sudden
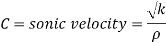
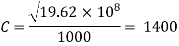
Rise in pressure
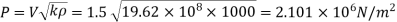
Q12) In a pipe 600 mm diameter and 3000 m length, provided with a valve at its end, water is flowing with a velocity of 2m's. Assuming velocity of pressure wave c= 1500m/s, find :) The rise in pressure if the valve is closed in 20 seconds, i) The rise in pressure if the valve is closed in 2.5 seconds. Assume the pipe to be rigid one and take bulk modulus of water as 2 GN/m².
A12)
D= 600 mm=0.6 m, L= 3000 m, V= 2 m/s, C = 1500 m/s, K = 2GN/m = 2x 10 Nm
Pipe is rigid.
To find: P
Case (i): Rise in pressure if valve is closed in 20 sec. t = 20 sec.
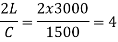
The ratio,
We know that if t>2L/C the valve is closed gradually. Rise in pressure (p) for gradually closure of valve
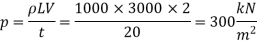
Case (ii): Rise in pressure, if valve is closed in 2.5 sec.
Since the valve is closed rapidly

Velocity of pressure wave
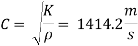
The ratio
2L/C = 2x3000/1414.2 = 4.24 sec
When pipe is rigid, the rise in pressure due to rapidly closed is given by.
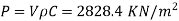
Q13) A 60 cm diameter steel pipe of 1.0 cm thickness and 300 m length carrying water is connected to a needle valve at the 0.3 second and 1 second respectively. d/s end and to the reservoir at the u/s end, has a head of 50 m. Determine the rise in pressure if the valve is closed in Take E=2.47 x 10"N/m²; E-2.075 x 10' N/m²
A13)
Given:
Diameter d = 60 cm,
Thickness t= 1 cm
Length L= 300 m Head h= 50 m
Time t₁ = 0.3 sec., t₂ = 1 sec.
E steel E= 2.47 x 10^11 N/m².
E water K = 2.075 x 10^9 N/m²
To find: dp
Effective bulk modulus of elasticity
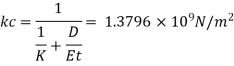
Velocity of pressure C
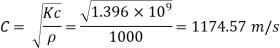
Critical time T₁
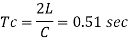
Velocity of flow in pipe by using Darcy's equation
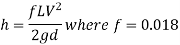
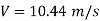
Since T<T, i.e. (0.3<0.51), the pressure rises due to sudden closure
Rise in pressure,
Dp = pCV = 1000 x 1174.57 x 10.44= 12.26 N/mm^2