Unit – 1

Set Theory and Logic

Question-1: Define discrete mathematics.

Sol. Computer science is all about the study of problems and solving problems by some process. The main goal is to develop an algorithm (a step by step list of some instructions in order to solve a certain problem).

According to K.H Rosen, discreet mathematics has more than one purpose but more importantly it equips computer science students with logical and mathematical skills.

By B.Miller and D. Ranum, A computing machine end is to develop an algorithm, a measure by step list of instructions in work outing a job. Algorithm are finite procedures that if followed will work out the job.

Question-2: What are sets and subsets?

Sol. Sets- A set is a collection of well-defined objects which are called the elements or members of the set.

We generally use capital letters to denote sets and lowercase letters for elements.

If any element which exists in the set is to be denoted as-

Suppose an element ‘a’ is from a set X, then it is represented as- a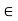X

Which means the element ‘a’ belongs to the set X.

If the element is not form the group then we use ‘not belongs to’.

Subsets-

Let every element of set X is also an element of a set Y, then X is said to be the subset of Y.

Symbolically it is written as-

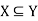
Which is read as- X is the subset of Y.

Note- If X = Y then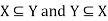

Question-3: Define equal sets and null sets.

Sol. Equal sets-

If X and Y are two sets such that every element of X is an element of Y and every element of Y is an element of X, the set and set Y will be equal always.

We write it as X = Y and read as X and Y are identical.

Null set-

A set which does not contain any element is known as null set.

We denote a null set by ∅

The null set is a subset of every set.

Question-4: If A = {1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8, 9} and C = {5, 6, 7, 8, 9, 10}

Then-

A∪B = {1, 2, 3, 4, 5, 6,7, 8, 9}

A∪C = {1, 2, 3, 4, 5, 6,7, 8, 9,10}

B∪C = {4, 5, 6,7, 8, 9, 10}

A∩B = {4, 5, 6}

A∩C = {5, 6}

B∩C = {5, 6, 7, 8, 9}

Question-5: Define Complements, differences and symmetric differences.

Sol. Complement-

The complementof a set A, denoted by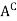 , is the set of elements which belong to U(universal set)but which do not belong to A. That is

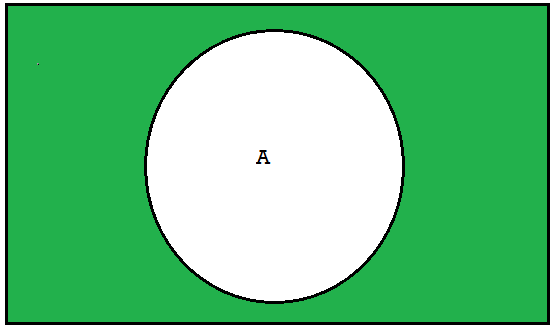
= {x | x ∈U, x /∈A}

Difference-

The differenceof A and B, denoted byA\B or A-B, is the set of elements which belong to A but which do not belong to Bthat is-

A-B = {x | x ∈A, x / ∈B}

The set A\Bor A-Bis read “A minus B”.

Symmetric difference-

The symmetric differenceof sets A and B, denoted by A⊕B, consists of those elements which belong to A or B but not to both. That is

A ⊕B = (A ∪B)-(A ∩B) or A ⊕B = (A-B) ∪(B-A)

Question-6: What do you understand by conjunction and disjunction?

Sol. Conjunction- p ⋀ q

Any two propositions can be combined by the word “and” to form a compound proposition called the conjunctionof the original propositions. Symbolically,

p∧q

Read “p and q,” denotes the conjunction of p and q. Since p ∧q is a proposition it has a truth value, and this truth

Value depends only on the truth values of p and q.

Note- If p and q are true, then p ∧q is true; otherwise p ∧q is false.

Disjunction, p ∨q

Any two propositions can be combined by the word “or” to form a compound proposition called the disjunctionof the original propositions. Symbolically,

p∨q

Read “p or q,” denotes the disjunction of p and q. The truth value of p ∨q depends only on the truth values of p

And q as follows-

If p and q are false, then p ∨q is false; otherwise p ∨q is true

Question-7: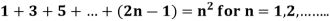

Sol. here for n = 1,     1 = 1²

Now let us assume that the statement is true for n = k

Hence we assume that 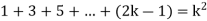is true.

Now we need to prove that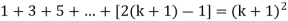

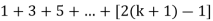
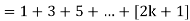
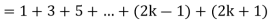
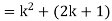
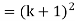
So that 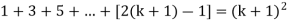which satisfies the second step.

Hence-

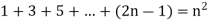
Question-8: Prove 1+2+...+n = n (n+1)/2 using a proof by induction

Sol.

Let n=1: 1 = 1(1+1)/2 = 1(2)/2 = 1 is true,

Step-1: Assume n=k holds: 1+2+...+k = k(k+1)/2

Show n=k+1 holds: 1+2+...+k+(k+1)=(k+1)((k+1)+1)/2 

Substitute k with k+1 in the formula to get these lines. Notice that I write out what I want to prove.

Step-2: Now start with the left side of the equation

1+2+...+(k+1)=1+2+...+k+(k+1)

=k(k+1)/2 + (k+1)

=(k(k+1)+2(k+1))/2 by 2/2=1 and distribution of division over addition

=(k+2)(k+1)/2 by distribution of multiplication over addition

=(k+1)(k+2)/2 by commutativity of multiplication

Question-9: Define power sets with example.

Sol.  Power sets-

The set of all subsets of a set A is called the power set of A.

The power set of A is denoted by P(A).

So that-

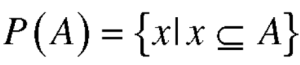
If A has n elements in it, then power set P(A) has 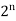elements.

Example: If A = {1, 2} then power set of A will be-

P(A) = {ϕ, {1}, {2}, {1, 2}}

Question-10: What is logical equivalence?

Sol. Two propositions P (p, q, . . .)and Q(p, q, . . .) are said to be logically equivalent, or simply equivalent and denoted by

P (p, q, . . .) ≡Q(p, q, . . .)

Note- the prepositions are logically equivalent.