Unit-2
Relations and Functions
Question-1 Define relations.
Sol.
Let X and Y are two sets, A relation from X to Y is a subset of 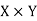 .
.
Now suppose R is a relation form X to Y, then R is a set of ordered pairs where each first element comes from X and each second element comes from Y.
For each pair 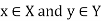 , one the following rule is true-
, one the following rule is true-
1. 
2.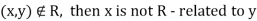
The domain of a relation R is the set of all first elements of the ordered pairs which belongs to R, and range is the second element.
Question-2: Define the composition of relations.
Sol.
Let X, Y and Z are three sets and R be a relation from X to Y and S is a relation from Y to Z.
So that R is a subset of 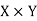 and S is a subset of
and S is a subset of 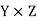 .
.
Then R and S give a relation form X to Z which is denoted by RoS,
And can be defined as follows-
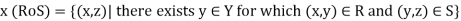
The relation RoS is called the composition of R and S.
Note- If R is a relation on a set A, that is, R is a relation from a set A to itself. Then the composition of R is RoR. Denoted by 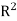 .
.
Question-3: A = {2, 3}, B = {3, 4, 5, 6} and R is a relation from A to B defined as follows-
(a, b) ∈R if “a divides b” Write the solution set of R.
Sol: 2 divides 4 and 2 divides 6
⇒(2, 4) ∈R and (2, 6) ∈R
3 divides 3, 3 divides 6
⇒(3, 3) ∈R and (3, 6) ∈R
4 divides 4 ⇒(4, 4) ∈R
Thus R = {(2, 4), (2, 6), (3, 3), (3, 6), (4, 4)}
Question-4: Let Z denote the set of integers and the relation R in Z be defined by “aRb” iffa – b is an even integer”. Then show that R is an equivalence relation.
Sol.
1. R is reflexive; since
∅ = a −a is even, hence aRa for every a∈Z.
2. R is symmetric:
If a – b is even then b – a = – (a – b) is also even hence aRb⇒bRa
3. R is transitive: for if aRb and bRc then both a – b and b – c are even.
Consequently, a – c = (a – b) + (b – c) is also even.
∴aRb and bRc⇒aR c
Thus, R is an equivalence relation.
Question-5: Let A = {1, 4, 5} and R = {(1, 4), (1, 5), (4, 1), (4, 4), (5, 5)}, find relation matrix of this relation.
Sol. we have-
R = {(1, 4), (1, 5), (4, 1), (4, 4), (5, 5)},
Then,
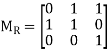
Question-6 Find the relation from the following digraph-
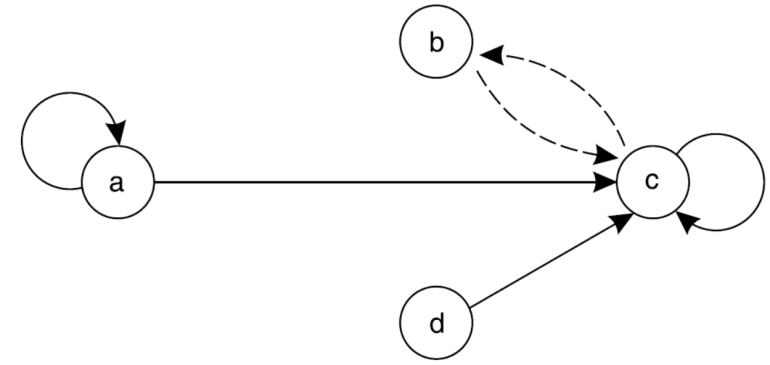
Sol. The relation R of the digraph is
R = {(a, a), (a, c), (b, c), (c, b), (c, c), (d, c)}
Question-7: Find the number of ways to partition of 10 peoples into four groups 
So that two teams contain 3 persons and two teams contain 2 persons.
Sol.
By using above theorem, we get-
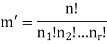
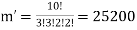 ordered partitions
ordered partitions
Here the group form an unordered partition so that we divide m’ by  Because of the two cells with three elements each and
Because of the two cells with three elements each and 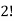 Because of the two cells with two elements each.
Because of the two cells with two elements each.
So that-
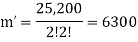
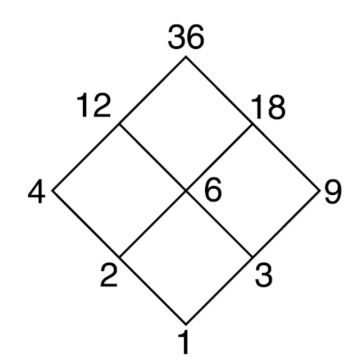
Question-8 Draw the Hasse diagram of positive division of 36.
Sol.
We have
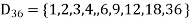
Suppose R is the partial order relation on 
The Hasse diagram will be-
Question-9 Define Lattices.
Sol.
Lattices-
A lattice is a partially ordered set 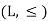 in which every pair of elements a,b
in which every pair of elements a,b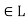 has a greatest lower bound and a least upper bound
has a greatest lower bound and a least upper bound
For example-
Suppose S be a non-empty set and L = P(S); 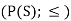 that means (
that means (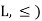 is partially ordered.
is partially ordered.
If X and Y are two elements of L, then-
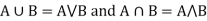
Hence (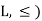 is a Lattice.
is a Lattice.
Axiomatic definition of Lattice-
Let L be a non-empty set closed under two binary operations denoted by ∧ and ∨.
Then L is said to be a Lattice if it follows the axioms given below, here a, b and c are the elements of L.
Question-10: Let (L, ≤) be a lattice in which ‘⋅’ And ‘+’ denote the operations of meet and join respectively.
Then
a≤b ⇔a ⋅b = a ⇔a + b = b ∀a, b, c ∈L
So:
Suppose a ≤b
As we know that a ≤a so that a ≤a.b but according to definition a.b≤a
So that- a ≤b ⇒a ⋅b = a
Let a ⋅b = a
But this is possible only if a ≤b which means a ⋅b = a ⇒a ≤b
∴a≤b⇒a ⋅b = a and a ⋅b = a ⇒a ≤b
Combine these two, we get
a≤b ⇔a ⋅b = a
Now let,
a⋅b = a,
Then we have
b + (a ⋅b) = b + a + a + b
But,
b + (a ⋅b) = b
Hence a + b = b
Similarly by assuming a + b = b
We can show that a ⋅b = a
Hence a ≤b ⇔a ⋅b = a ⇔a + b = b = a
Question-11 Suppose A = {1, 2, 3, 4} and B = {a, b, c, d, e, f} consider the relation
R = {(1, a), (1, c), (1, e), (2, b), (2, d), (2, f), (3, c), (3, d), (4, a), (4, f)}
Sol.
Let,
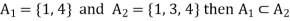
And,


So that-

Thus-

Question-12 Show that the inverse of an invertible mapping is unique.
Sol
Let 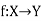
By any invertible mapping,
Let,
g: Y→X
h: Y→X
are two different inverse mapping of f.
Let y ∈ Y and 
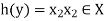
Now-
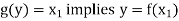
And
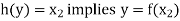
so that-
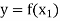 and
and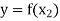
Now-
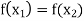
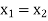
Which shows that g(y) = h(y)∀ y ∈ Y
So that the inverse of f is unique.