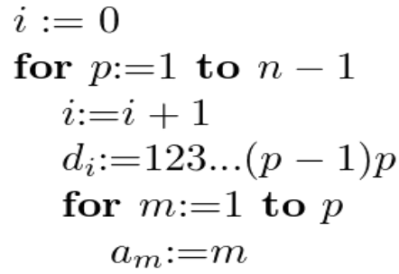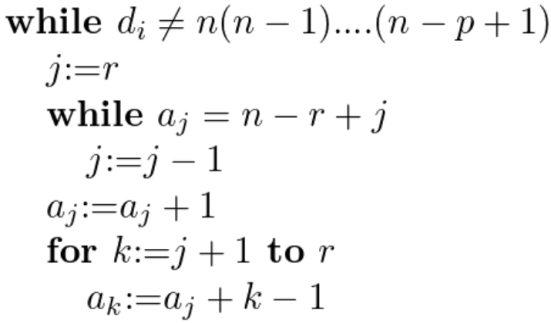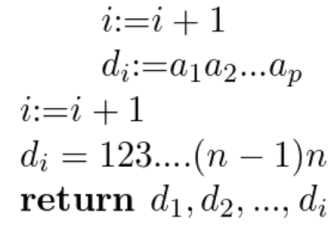Unit-3

Counting Principles

Question-1: In how ways can be drawn an ace or a king from an ordinary deck of playing cards?

Sol.

Number of Aces in a pack = 4

Number of kings in a pack = 4

Number ways an Ace or a king can be drawn from the pack = 4 + 4 =

Question-2: Define product rule

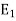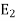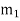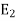Sol.If , , …, En are events, and E can happen in ways can happen 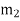ways, … 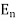can happen in 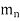ways, then the sequence of events E, first followe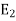d by followed by , …, followed by 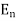can happenin m1 × m2 × … × mn ways

Question-3: Define permutation.

Sol.

The arrangement of a set of n objects in a given order is called a permutation.

Any arrangement of any 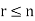of these objects in a given order is said to be r-permutation.

The number of permutations of n objects taken r will be denoted as-

P(n, r)

Formula-                                

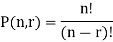
Question-4: Three cards are chosen one after the other from a 52-card deck. Find the number m of ways

This can be done: (a) with replacement; (b) without replacement.

Sol.

(a) Each card can be chosen in 52 ways. Thus m = 52(52) (52) = 140 608.

(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-

P(52, 3) = 52(51)(50) = 132600

Question-5: A box contains 10 light bulbs. Find the number n of ordered samples of:

(a) Size 3 with replacement,

(b) Size 3 without replacement.

Solution:

(a) n=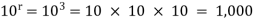

(b) P (10, 3) = 10 × 9 × 8 = 720

Question-6: Define combinations and its properties.

Sol. A combination of n objects taken at a time is an unordered selection of r of the n

Objects (r ≤n).

A combination of n objects taken r at a time is also called r-combination of n objects.

The number of combinations is given by-

C(n, r)

Note-

1. property-1

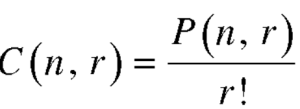
2. property-2

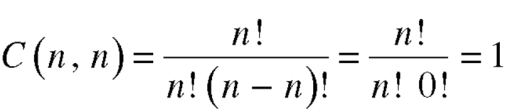
3. property-3

Question-7: Find the term containing in the expansion of

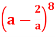
Sol.

The general term will be-

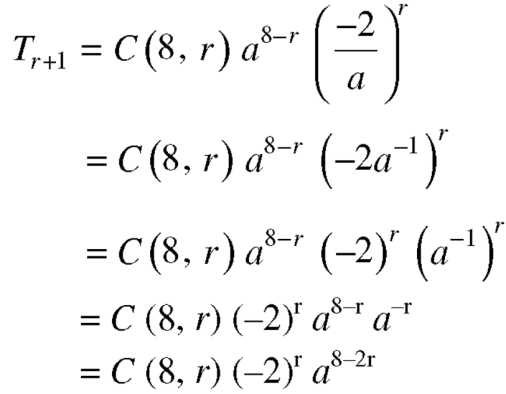
Put 8 – 2r = 4 we get r = 2

Therefore the term contains is-

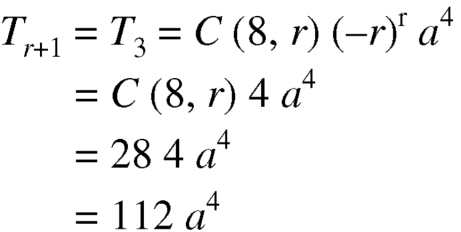
Question-8: Expand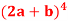

Sol.

Here we have-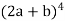

 By using binomial theorem, we get

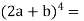
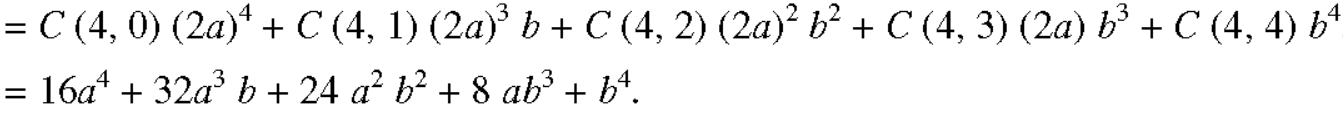
Question-9: Find the number of ways of placing 8 similar balls in 5 numbered boxes.

Solution:

The number of ways of placing similar balls in 5 numbered boxes is

= C (5 – 1 + 8, 8)

= C (12, 8) = 495

Question-10: How many outcomes are possible by costing a 6 faced die 10 times?

Solution:

This is same as placing 10 similar balls into 6 numbered boxes.

There are C (6 – 1 + 10, 10)

= C (15, 10) possible outcomes.

Question-11: Describe an algorithm for generating all the combinations of the set of the n smallest positive integers-

Sol.