UNIT-5

TREES

Q 1: Every binary tree has an odd no. Of  vertices.

Solution: let T = (V, E) be a binary tree.

A part from the root every vertex in a binary tree is an odd degree.

w.k.t., there must be an even no. of vertices such odd degree.

When the root which of odd degree is added to this even no. Of vertices i.e.,

Even no. of vertices and one root vertex, we have odd no. Of vertices.

Therefore, every binary tree has odd no. of vertices

Note: let a tree has ‘n’ vertices and ‘m’ pendent vertices, then the no. of internal vertices of degree 3 is n-(m+1).

Q 2: prove that there are 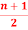pendent vertices in any binary tree with ‘n’ vertices.

Solution: suppose T = (V, E) be a binary tree with ‘n’ vertices. Let ‘m’ be the two no. of pendent vertices in T. Then T has (n-(m+1)) no. of internal vertices of degree 3

So, the sum of degree of all vertices in T is 3(n-m-1) + m+2….(1)

Since T  is tree with ’n’ vertices then it has (n-1) edges.

So, the degree sum of ‘n’ vertices in T is given by

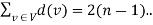(2)

From (1) and (2)

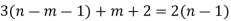
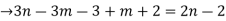
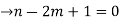
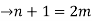
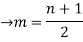
  The no.of pendent vertices in binary tree is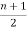 

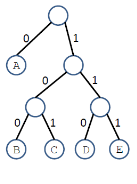
Q 3: Find the tree traversal for the following binary tree.

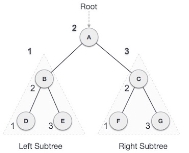
Solution: we follow the known three steps to get the final tree traverse i.e.,

Step-1: In-order Traversal

In this traversal method, the left sub tree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a sub tree itself.

If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.

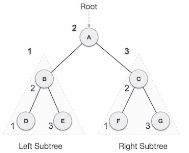
We start from A, and following in-order traversal, we move to its left subtree B. B is also traversed in-order. The process goes on until all the nodes are visited.

The required tree-traversal is the following order.

D → B → E →A→ F → C → G

Algorithm

Step-1: Recursively traverse left sub tree

Step -2: visit root node

Step-3: Recursively traverse right sub-tree.

We will continue this process until all nodes are traversed.

Step-2:Pre-order Traversal

In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.

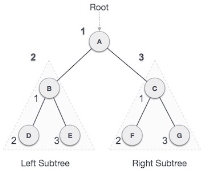
We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited.

The required tree traversal is the following order.

A → B → D → E → C → F → G

Algorithm:

Step-1: Visit root node.

Step-2: Recursively traverse left sub-tree.

Step-3: Recursively traverse right sub-tree.

Step-3:Post-order Traversal

In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node.

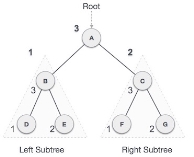
We start from A, and following Post-order traversal, we first visit the left sub-tree B. B is also traversed post-order. The process goes on until all the nodes are visited. The output of post-order traversal of this tree will be −

D → E → B → F → G → C → A

Algorithm:

Step-1: Recursively traverse left sub-tree.

Step-2: Recursively traverse right sub-tree.

Step-3: Visit root node.

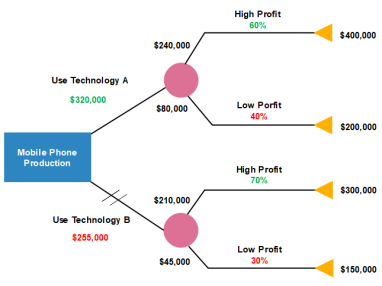
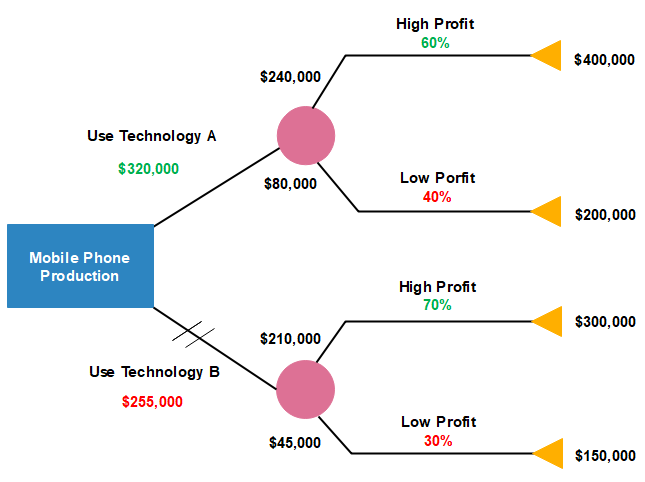
Q 4: Draw the decision tree for the below data.

A company has mobile production process by using two-technologies A and B namely. Where the details are given below

Technology A: The cost for using this technology is $ 320,000 and we have two processes which gain 60 % and 40 % profit respectively.

By using decision tree classify the following.

Technology B:

Solution: The cost for using this technology is $255,000 and we have two processes which gain 70 % and 30 % profit respectively.

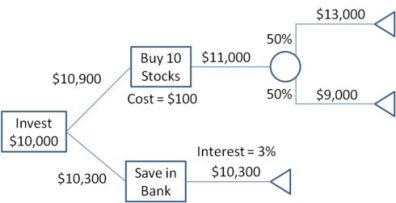
Q 5: Draw a decision tree for the following data.

A person gets $ 10,300 by saving inbank and conversely he gets $ 13000 and @ 9,000 by buying stocks so draw the decision tree for the given data and express which method is best to earn more income

Solution:

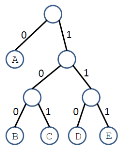
Q 6:

E.g.,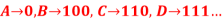

Given the frequencies of each character, design the optimal pre-fix code whose en-coded text requires the least storage. We want to find a pre-fix code tree that corresponds to an optimal pre-fix code.

Solution:

Step 1: In an optimal pre-fix code tree, each internal node must have two children.

The above tree is not an optimal pre-fix code tree.

Step 2: To get an optimal pre-fix code tree the leaves must be corresponding to the least frequent characters which are siblings, and the leaves are farthest from the root.

For this we consider an optimal pre-fix code tree.

Let y and z be the least frequent characters.

Let x be a character whose leaf is farthest from the root( its sibling g must be a leaf for some character ‘x’).

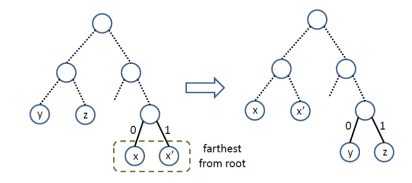
Is the required optimal pre-fix tree.

Q 7: Suppose the relative frequencies as follows:

Step-1:                               Step-2:                                         Step-3:

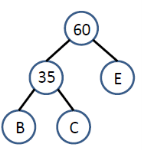
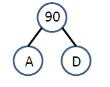
Step-4: finally the Huffman coding is represented in the below tree.

Cut sets:Let 'G'= (V, E) be a connected graph. A subset E' of E is called a cut set of G if deletion of all the edges of E' from G makes G disconnect.

If deleting a certain number of edges from a graph makes it disconnected, then those deleted edges are called the cut set of the graph.

Q 8: Take a look at the following graph. Its cut set is E1 = {e1, e3, e5, e8}.

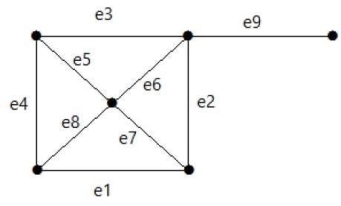
Solution:

After removing the cut set E1 from the graph, it would appear as follows −

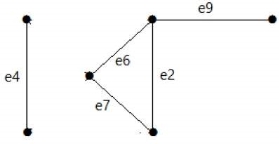
Similarly there are other cut sets that can disconnect the graph –

Q 9: For instance, identify the minimum spanning tree from the following graph G by using the Kruskal’s algorithm.

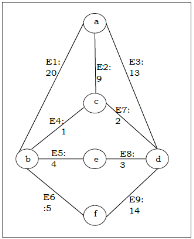
SOLUTION:

The following table is constructed from the above graph:

In accordance with the weight of the Edge, the table is rearranged in ascending order.

We get the required minimal spanning tree

Step-1:

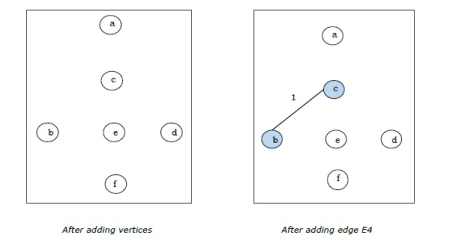
Step-2:

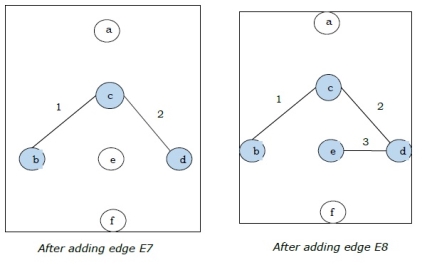
Step-3:

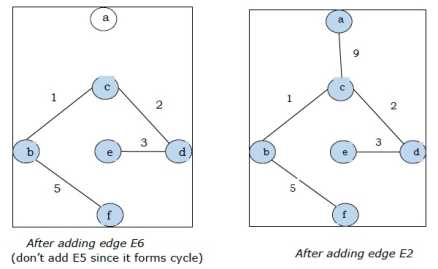
As all the edges are covered in the last figure, the algorithm is stopped and this is considered as the minimal spanning tree and the total weight of the spanning tree is (1+2+3+5+9)=20.

Q 10: For instance, consider the following graph G and identify the minimum spanning tree using Prim’s algorithm

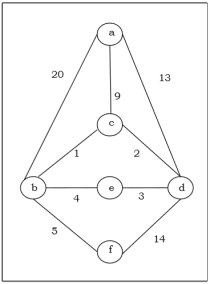
Solution:

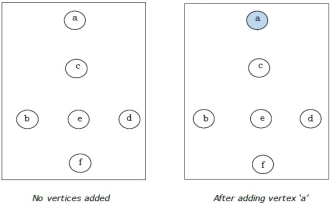
It is started with vertex ‘a’.

Step-1:

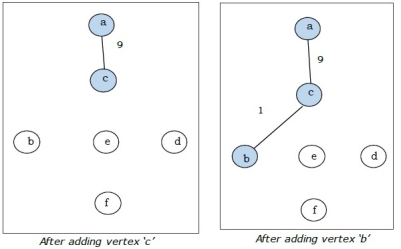
Step-2:

Step-3:

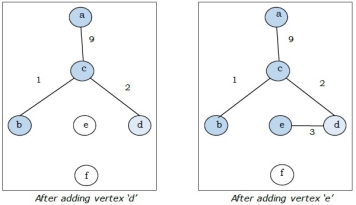
Step-4:

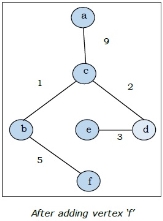
The above graph is the minimum spanning tree and the total weight is

(1+2+3+5+9)=20

Q 11: Find the minimum flow of the given graph.

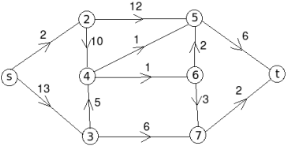
Solution:

Let the edge-labels on the graphs G represent capacity(flow).

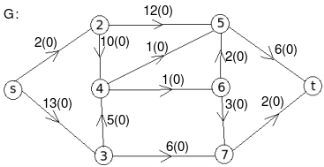
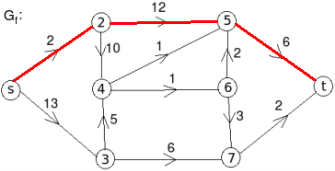
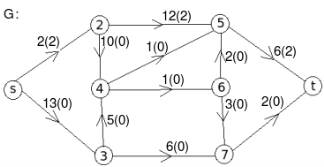
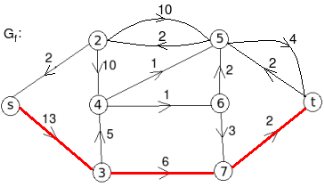
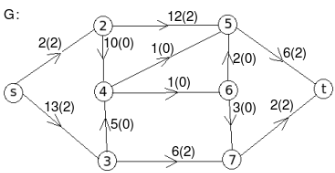
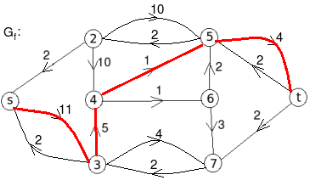
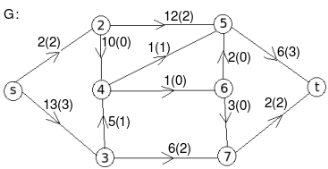
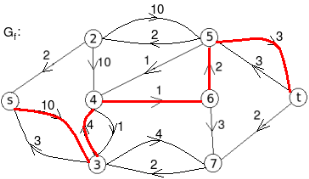
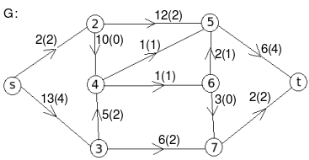
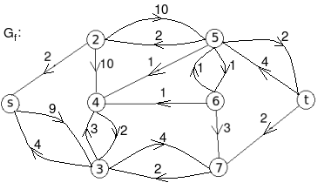
The minimum cut is highlighted in green.

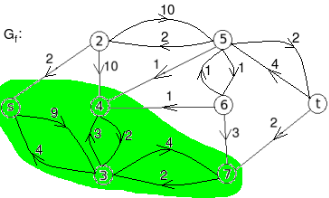
Therefore, the minimum cut has capacity 6 and the maximum flow has flow 6.