Unit-VI
Algebraic Structures and Coding Theory
Q1: Solve the following system of equations
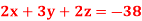 … (1)
… (1)
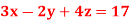 …. (2)
…. (2)
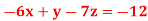 …. (3)
…. (3)
Solution:
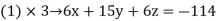
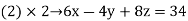
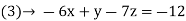
By solving the above equations, we get
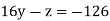
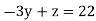
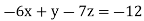
Solving for z we get
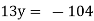
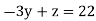
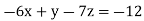
We get y = -8
By putting y value in above equation, we get z=-2
And inserting both the equations we solve for x, we get x= 3
Therefore the solution to the system of equation is x = 3, y = -8, z = -2
Q 2: Let S=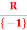 . Define * on S by a*b =a+ b+ a b
. Define * on S by a*b =a+ b+ a b
(a) Show that * is a binary operation on S.
(b) Show that [S, *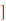 is a group.
is a group.
(c) Find the solution of the equation 2*x*3= 7 in S
Solution: (a) We must show that S is closed under *, that is , that a+b+ab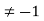 for a,b
for a,b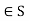 .Now a+b+ab=-1 if and only if 0=ab+a+b+1=(a+1)(b+1).This is the case if and only if either a=-1 or b = -1 , which is not the case for a,b
.Now a+b+ab=-1 if and only if 0=ab+a+b+1=(a+1)(b+1).This is the case if and only if either a=-1 or b = -1 , which is not the case for a,b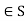 .
.
(b) We have a*(b*c) = a*(b+c+bc) = a+(b+c+bc)+a(b+c+bc)=a+b+c+ab+ac+bc+abc and (a*b)*c = (a+b+ab)*c =(a+b+ab)+c+(a+b+ab) = a+b+c+ab+ac+bc+abc. Thus * is associative. Note that 0 acts as identity element for *, since 0*a =a*0=a.
Also, 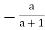 acts as inverse of a , for a*
acts as inverse of a , for a* 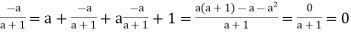
Thus [s, *] is a group.
(c)Because the operation is commutative, 2*x*3=2*3*x=11*x. Now the inverse of 11 is 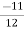 ,by part(b). from 11*x=7, we obtain
,by part(b). from 11*x=7, we obtain
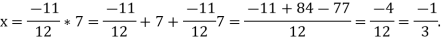
Q 3: Let G be a group with a finite number of elements. Show that for any 
Solution: Let G has m elements, Then the elements e, a,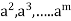 are not all different, since G has only m element. If one of e, a,
are not all different, since G has only m element. If one of e, a,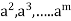 is e, then we are done. If not, then we must have
is e, then we are done. If not, then we must have 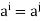 where i<j, Repeated left cancellation of a yields e=
where i<j, Repeated left cancellation of a yields e=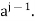
Example 1: Let 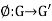 be a group homomorphism , and let H=ker(
be a group homomorphism , and let H=ker(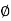 ).Let a
).Let a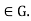 Then , the set
Then , the set 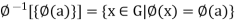 is the left coset aH of H, and is also the right coset Ha of H , Consequently , the two partitions of G into left cossets and into right cossets of H are the same.
is the left coset aH of H, and is also the right coset Ha of H , Consequently , the two partitions of G into left cossets and into right cossets of H are the same.
Proof: (a) It is a homomorphism, because 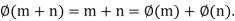
(b) It is not a homomorphism, because 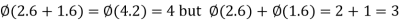 .
.
(c) It is a homomorphism, because 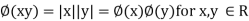 *
*
(d) It is a homomorphism, because 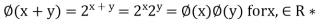
Q 4: The following are three equivalent conditions for a subgroup H to be a normal subgroup of a group G.
1.
2.
3.
Proof: (1)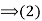 Suppose that H is a subgroup of G such that
Suppose that H is a subgroup of G such that 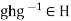 for all g
for all g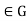 and all h
and all h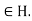 Then
Then 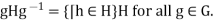
We claim that actually 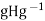 =H.We must show that H
=H.We must show that H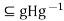 for all g
for all g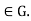
Let h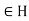 . Replacing g by
. Replacing g by 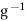 in the relation
in the relation 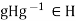 , we obtain
, we obtain 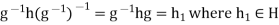 .
.
Consequently,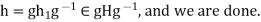
(3)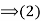 Suppose that gH=Hg for all g
Suppose that gH=Hg for all g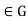 . Then
. Then 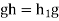 , So
, So 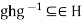 for all g
for all g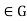
And all 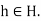 By the preceding paragraph, this means that
By the preceding paragraph, this means that 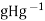 =H for all g
=H for all g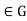 .
.
(2)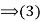 Conversely, if
Conversely, if 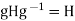 for all g
for all g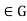 then
then 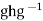 =
=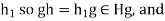 gH
gH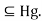 But also,
But also, 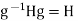 giving
giving 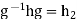 ,so that hg=g
,so that hg=g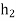 and Hg
and Hg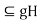 .
.
Q 5: Prove that congruence modulo n is an equivalence relation on Z.
Solution:
1) Reflexivity: For any a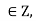 we have
we have 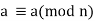 because a-a = 0 is divisible by n.hence relation is reflexive.
because a-a = 0 is divisible by n.hence relation is reflexive.
2) Symmetry: suppose a  b (mod n)
b (mod n)
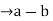 is divisible by n
is divisible by n 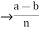 = k, for some k
= k, for some k 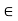 z
z 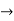 a-b = nk
a-b = nk
Therefore, b-a = - (a-b) = -nk= n (-k)
Thus, the relation is symmetric.
3) Transitivity: Suppose a  b (mod n) and b
b (mod n) and b  c (mod n), then
c (mod n), then 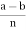 = k and
= k and 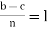
By adding these two equations we get, a-c = n (k+1) 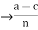 = k+l
= k+l
So, a-c is divisible by n as k+1 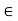 Z, i.e., a
Z, i.e., a  c (mod n)
c (mod n)
Thus, the relation is transitive.
Hence this is an equivalence relation on Z.
Example1: The cancellation laws hold in a ring R if and only if R has no divisors of 0.
Proof : Assume that R is a ring in which the cancellation laws hold and let ab=0 for some a, b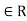 .If a
.If a by right cancellation law .Thus R has no divisors of 0, if the cancellation laws hold in R.
by right cancellation law .Thus R has no divisors of 0, if the cancellation laws hold in R.
Conversely, suppose that R has no divisors of 0, and suppose that ab=ac, with a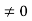 . Since a
. Since a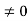 and since R has no divisors of 0, we have 0=ab-ac=a(c)
and since R has no divisors of 0, we have 0=ab-ac=a(c) 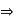 b-c =0
b-c =0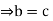 .In similar way, b a=ca with a
.In similar way, b a=ca with a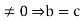 . Thus, if R has no divisors of 0, The cancellation laws hold in R.
. Thus, if R has no divisors of 0, The cancellation laws hold in R.
Q 6: Every field F is an integral domain.
Proof: Let 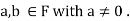 Assume that ab=0. Since
Assume that ab=0. Since 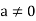 , the multiplicative we
, the multiplicative we
inverse 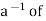 a exists, multiplying the above equation on both sides by
a exists, multiplying the above equation on both sides by 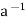 , weget
, weget
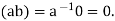 This implies, 0=
This implies, 0=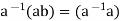 b=eb=b, Which shows that F has
b=eb=b, Which shows that F has
no divisors of 0. Since F is a field, in particular F is a commutative ring with unity, and we showed that F has no divisors of 0. Hence F is an integral domain.
We know that Z is an integral domain, but not a field. We next prove that finite integral domains are fields.
Example 3: Consider the map det of 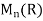 into R where det(A) is the determinant of the matrix A for A
into R where det(A) is the determinant of the matrix A for A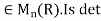 a ring homomorphism ? Justify your answer.
a ring homomorphism ? Justify your answer.
Solution: Because det(A+B) need not equal det(A)+det(B) , we say that det is not a ring homomorphism .For example ,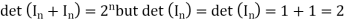
Q 7: Find the following binary operation by using code theory.
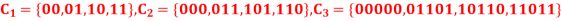
Solution: 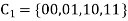
Is a binary [2,2] code for 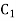 with generator matrix is
with generator matrix is
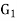 =
=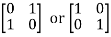 or…..
or…..
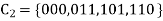
Is a binary [3,2] code for 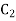 with generator matrix is
with generator matrix is
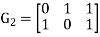
And 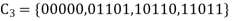
Is a binary [5,2] code for 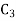 with generator matrix is
with generator matrix is
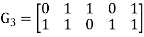
Q 8: Consider the polynomial code over GF(2)={0,1} with n=5 , m=2 and generator polynomial 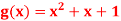 , This code consists of the following code words.
, This code consists of the following code words.
Solution 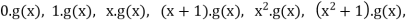
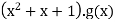
Or written explicitly:
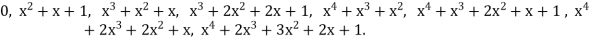
Since the polynomial code is defined over the Binary Galois Field GF(2)={0,1}, polynomial elements are represented as a modulo-2 sum and the fail polynomials are:
0, 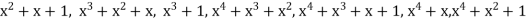
Equivalently, expressed as strings of binary digits, the code words are
00000, 00111, 01110, 01001, 11100, 11011,10010, 10101.
This as every polynomial cod, is indeed a linear code, i.e. linear combinations of code words are again code words. In case like this where the field is GF (2), linear Combinations are found by taking the X or the code words expressed in binary form (e.g. 00111 XOR 10010=10101)
Q 9: (Theorem): The matrix ideals of the ring Z of integers are the principal ideals generated by prime integers.
Proof: Every ideal of Z is principal. Consider a principal ideal (n), with 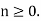 If n is a prime , say n=p , then
If n is a prime , say n=p , then 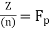 , a field , the ideal (n) is maximal , If n is not prime , there are three possibilities : n=0, n=1 , or n factors . Neither the zero ideal nor the unit ideal is maximal. If n factors, say n=ab, with 1<a<n, then 1
, a field , the ideal (n) is maximal , If n is not prime , there are three possibilities : n=0, n=1 , or n factors . Neither the zero ideal nor the unit ideal is maximal. If n factors, say n=ab, with 1<a<n, then 1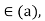 therefore (n) < (a)<(1). The ideal (n) is not maximal.
therefore (n) < (a)<(1). The ideal (n) is not maximal.
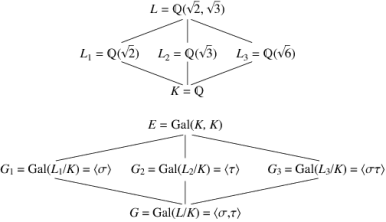
Q 10: Fundamental theorem of Galois Theory:
Statement: For a Galois extension field K of field F, the fundamental theorem of Galois Theory sates that the subgroups, of the Galois group G = Gal (K/F) correspond with the sub-field K containing F. If the sub-field L corresponds to subgroup H, then the extension field degree K over L is the group order of H.
Proof:
Given 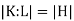
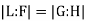
Suppose 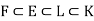 , then E and L corresponds to subgroups HE and HL of G such that HE is a subgroup of HL. Also, HE is a normal subgroup iff E is a Galois extension field. Since any subfield of a separable extension, which the Galois extension field K must be separable.
, then E and L corresponds to subgroups HE and HL of G such that HE is a subgroup of HL. Also, HE is a normal subgroup iff E is a Galois extension field. Since any subfield of a separable extension, which the Galois extension field K must be separable.
Then E is Galois iff E is a normal extension of F. So normal extensions correspond to normal subgroups. When HE is normal then,
Gal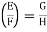
As the quotient group of the group action of G on K.
Q 11: Let E = Q (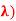 be the field of rational functions in
be the field of rational functions in  and let
and let
G = 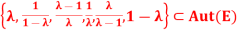
Which is a group under composition, isomorphic to S3?
Solution: Let F be the fixed field of g, then
Gal (E/F) = G
If H is a subgroup of G then co-efficient of the following polynomial are given by
P (T) = 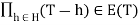
Generate the fixed field H.
Galois correspondence means that every subfield of E/F can be constructed this way.
Example if H= 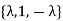 then the fixed field is Q (
then the fixed field is Q (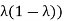 and if H =
and if H = 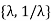 then the fixed field is Q (
then the fixed field is Q (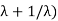 .
.
Likewise one can write F, the fixed field of G as Q (j) where j is j-invariant.