undefined | unit 1 introduction to algorithm and data structures

FDS

UNIT 1

QUESTIONS

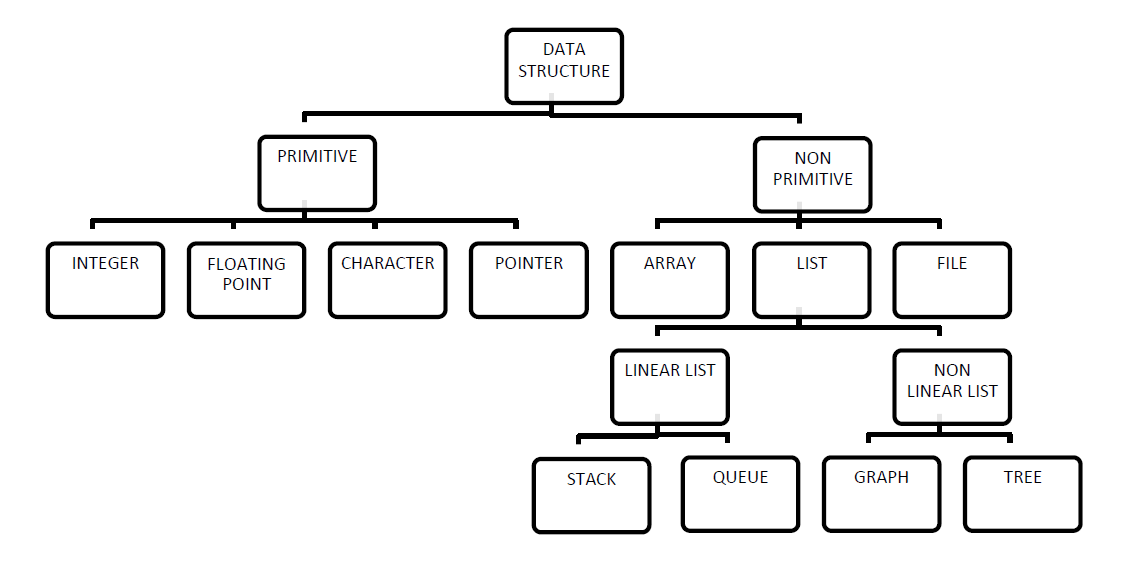
Q1 What are types of data structures?

Data structures

• Data structure could also be a representation of the logical relationship existing between individual elements of knowledge.

• Data Structure may be a way of organizing all data items that considers not only the weather stored but also their relationship to every other.

• We also can define arrangement as a mathematical or logical model of a specific organization of knowledge items.

• The representation of particular arrangement within the main memory of a computer is named as storage structure.

• The storage structure representation in auxiliary memory is named as file structure.

• It is defined because the way of storing and manipulating data in organized form in order that it are often used efficiently.

• Data Structure mainly specifies the subsequent four things

Organization of knowledge

Accessing methods

Degree of associativity

Processing alternatives for information

• Algorithm + arrangement = Program

Data structure study covers the subsequent points

Amount of memory require to store.

Amount of your time require to process.

Representation of knowledge in memory.

Operations performed thereon data.

Data Structures are normally classified into two broad categories

Primitive arrangement

Non-primitive arrangement

$C:\Users\Kilua Zoldyck\Pictures\adt.png$

Data types a specific quite data item, as defined by the values it can take, the programming language used, or the operations which will be performed thereon.

1. Primitive arrangement

• Primitive data structures are basic structures and are directly operated upon by machine instructions.

• Primitive data structures have different representations on different computers.

• Integers, floats, character and pointers are samples of primitive data structures.

• These data types are available in most programming languages as inbuilt type.

Integer: it is a knowledge type which allows all values without fraction part. We will use it for whole numbers.

Float: it is a knowledge type which use for storing fractional numbers.

Character: it is a knowledge type which is used for character values.

Pointer: A variable that holds memory address of another variable are called pointer.

Non primitive Data Type

• These are more sophisticated data structures.

• These are derived from primitive data structures.

• The non-primitive data structures emphasize on structuring of a gaggle of homogeneous or heterogeneous data items.

• Examples of Non-primitive data type are Array, List, and File etc.

• A Non-primitive data type is further divided into Linear and Non-Linear arrangement

• Array: An array could also be a fixed-size sequenced collection of elements of the same data type.

• List: An ordered set containing variable number of elements is known as Lists.

• File: A file may be a collection of logically related information. It are often viewed as an outsized list of records consisting of varied fields.

Q2 What is algorithm and explain any simple daily life algorithm

An algorithm is procedure consisting of a finite set of unambiguous rules (instructions)which specify a finite sequence of operations that provides the solution to a problem, orto a specific class of problems for any allowable set of input quantities (if there are inputs). In other word, an algorithm is a step-by-step procedure to solve a givenproblem

A procedure is a finite sequence of well-defined instructions, each of which can bemechanically carried out in a finite amount of time.

Algorithm

• An essential aspect to data structures is algorithms.

• Data structures are implemented using algorithms.

• An algorithm may be a procedure that you simply can write as a C function or program, or the other language.

• An algorithm states explicitly how the info are going to be manipulated.

Algorithm Efficiency

• Some algorithms are more efficient than others. We might prefer to settle on an efficient algorithm, so it might be nice to possess metrics for comparing algorithm efficiency.

• The complexity of an algorithm may be a function describing the efficiency of the algorithm in terms of the quantity of knowledge the algorithm must process.

• Usually there are natural units for the domain and range of this function. There are two main complexity measures of the efficiency of an algorithm

Time complexity

• Time Complexity may be a function describing the quantity of your time an algorithm takes in terms of the quantity of input to the algorithm.

• "Time" can mean the quantity of memory accesses performed, the quantity of comparisons between integers, the quantity of times some inner loop is executed, or another natural unit related to the quantity of real time the algorithm will take.

Space complexity

• Space complexity may be a function describing the quantity of memory (space) an algorithm takes in terms of the quantity of input to the algorithm. We often speak of "extra" memory needed, not counting the memory needed to store the input itself.

• Space complexity is usually ignored because the space used is minimal and/or obvious, but sometimes it becomes as important a drag as time.

Algorithm to make a cake

"4 extra large eggs, beaten

1&1/2 C. stock

1/2 teaspoon salt

1 scallion, minced

1 C. small shrimp or lobster flakes

1 t. soy sauce

1 Tablespoon oil

1. Mix all the ingredients, except the oil, in a deep bowl.

2. Put 1" water in wide pot, then place deep bowl of batter inside.

3. Cover pot tightly and steam 15 min.

4. Heat oil very hot and pour over custard.

5. Steam 5 more min. Serves 4 people"

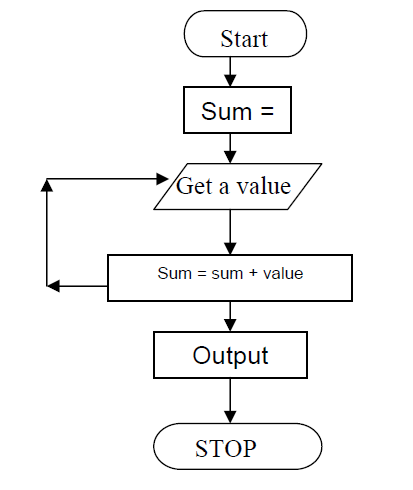
Q3 Explain pseudo code use of flowchart with example

Flowcharts and pseudocode

PSEUDOCODE
Pseudo code is one among the tools which will be want to write a preliminary plan which will bedeveloped into a computer virus. Pseudo code may be a generic way of describing an
algorithm without use of any specific programming language syntax. It is, because the namesuggests, pseudo code —it can't be executed on a true computer, but it models andresembles real programming code, and is written at roughly an equivalent level of detail.

Flowcharting may be a tool developed within the industry, for showing the steps
involved during a process. A flowchart may be a diagram made from boxes, diamonds and othershapes, connected by arrows - each shape represents a step within the process, and therefore the arrows
show the order during which they occur. Flowcharting combines symbols and flow lines, toshow figuratively the operation of an algorithm.

$C:\Users\Kilua Zoldyck\Pictures\1.png$

$C:\Users\Kilua Zoldyck\Pictures\2.png$

1. Start

2. Sum = 0

3. Get a value

4. Sum = sum + value

5. Go to step 3 to get next Value

6. Output the sum

7. Stop

$C:\Users\Kilua Zoldyck\Pictures\c.png$

Q4 Explain time and space complexities and asymptotic notations

Time complexity

• Time Complexity may be a function describing the quantity of your time an algorithm takes in terms of the quantity of input to the algorithm.

Space complexity

• Space complexity is usually ignored because the space used is minimal and/or obvious, but sometimes it becomes as important a drag as time.

Asymptotic Notations

When it involves analyzing the complexity of any algorithm in terms of your time and space, we will never provide a particular number to define the time required and therefore the space required by the algorithm, instead we express it using some standard notations, also referred to as Asymptotic Notations.

When we analyze any algorithm, we generally get a formula to represent the quantity of your time required for execution or the time required by the pc to run the lines of code of the algorithm, number of memory accesses, number of comparisons, temporary variables occupying memory space etc. This formula often contains unimportant details that do not really tell us anything about the time period .

Types of Asymptotic Notations

We use three sorts of asymptotic notations to represent the expansion of any algorithm, as input increases:

1. Big Theta (Θ)

2. Big Oh(O)

3. Big Omega (Ω)

Tight Bounds: Theta

When we say tight bounds, we mean that the time complexity represented by the Big-Θ notation is just like the average value or range within which the particular time of execution of the algorithm are going to be.

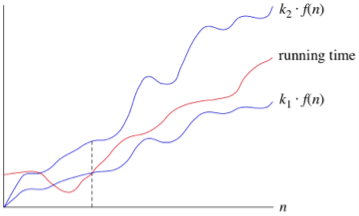
Big thets representation

Upper Bounds: Big-O

This notation is understood because the boundary of the algorithm, or a Worst Case of an algorithm.

It tells us that a particular function will never exceed a specified time for any value of input n.

The question is why we'd like this representation once we have already got the big-Θ notation, which represents the tightly bound time period for any algorithm. Let's take a little example to know this.

Lower Bounds: Omega

Big Omega notation is employed to define the boundary of any algorithm or we will say the simplest case of any algorithm.

This always indicates the minimum time required for any algorithm for all input values, therefore the simplest case of any algorithm.

In simple words, once we represent a time complexity for any algorithm within the sort of big-Ω, we mean that the algorithm will take at least this much time to complete its execution. It can definitely take longer than this too.

Space Complexity of Algorithms

Whenever an answer to a drag is written some memory is required to finish. For any algorithm memory could also be used for the following:

Variables (This include the constant values, temporary values)

Program Instruction

Execution

Space complexity is that the amount of memory employed by the algorithm (including the input values to the algorithm) to execute and produce the result.

Sometime Auxiliary Space is confused with Space Complexity. But Auxiliary Space is that the extra space or the temporary space employed by the algorithm during its execution.

Space Complexity = Auxiliary Space + Input space

Memory Usage while Execution

While executing, algorithm uses memory space for 3 reasons:

Instruction Space

It's the amount of memory wont to save the compiled version of instructions.

Environmental Stack

Sometimes an algorithm (function) could also be called inside another algorithm(function). In such a situation, the present variables are pushed onto the system stack, where they await further execution then the decision to the within algorithm (function) is formed.

Data Space

Amount of space employed by the variables and constants.

But while calculating the Space Complexity of any algorithm, we usually consider only Data Space and that we neglect the Instruction Space and Environmental Stack.

Q5 Explain greedy algorithm and divide and conquer algorithm

Greedy Algorithm

To begin with, the answer set (containing answers) is empty.

At each step, an item is added into the answer set.

If the answer set is possible, the present item is kept.

Else, the item is rejected and never considered again.

Problem: You have to make a change of an amount using the smallest possible number of coins.

Amount: $28

Available coins:

$5 coin

$2 coin

$1 coin

Solution:

Create an empty solution-set = { }.

coins = {5, 2, 1}

sum = 0

While sum ≠ 28, do the following.

Select a coin C from coins such that sum + C < 28.

If C + sum > 28, return no solution.

Else, sum = sum + C.

Add C to solution-set.

Up to the first 5 iterations, the solution set contains 5 $5 coins. After that, we get 1 $2 coin and finally, 1 $1 coin.

Greedy Algorithm Applications

Selection Sort

Knapsack Problem

Minimum Spanning Tree

Single-Source Shortest Path Problem

Job Scheduling Problem

Prim's Minimal Spanning Tree Algorithm

Kruskal's Minimal Spanning Tree Algorithm

Dijkstra's Minimal Spanning Tree Algorithm

Huffman Coding

Ford-Fulkerson Algorithm

Divide and Conquer Algorithm

A divide and conquer algorithm may be a strategy of solving an outsized problem bybreaking the matter into smaller sub-problems
solving the sub-problems, andcombining them to urge the specified output.

Here are the steps involved:

Divide: Divide the given problem into sub-problems using recursion.

Conquer: Solve the smaller sub-problems recursively. If the subproblem is little enough, then solve it directly.

Combine: Combine the answer s of the sub-problems which is a component of the recursive process to urge the solution to the particular problem.

Complexity

The complexity of the divide and conquer algorithm is calculated using the master theorem.

The divide and conquer approach divides a drag into smaller sub problems, these sub problems are further solved recursively.

The results of each sub problem isn't stored for future reference, whereas, during a dynamic approach, the results of each sub problem is stored for future reference.

Use the divide and conquer approach when an equivalent sub problem isn't solved multiple times. Use the dynamic approach when the results of a subproblem is to be used multiple times within the future.

Advantage of Divide and Conquer Algorithm

The complexity for the multiplication of two matrices using the naive method is O(n3), whereas using the divide and conquer approach (ie. Strassen's matrix multiplication) is O(n2.8074).

Other problems like the Tower of Hanoi also are simplified by this approach.

This approach is suitable for multiprocessing systems.

It makes efficient use of memory caches.

Divide and Conquer Application

Binary Search

Merge Sort

Quick Sort

Strassen's Matrix multiplication

Karatsuba Algorithm

Q6 What is problem and what are the steps to resolve a problem?

Problem

Analyzing algorithms: - analyzing algorithm has come to predicting the resources such as memory, communication bandwidth that the algorithm requires.

Goal of analysis: - Better utilization of memory, speed up the process (reduce the execution time)and reducethe development cost.

Running time of an algorithm: - Running time on a particular input is the numbers of basic operations that are perform.

It is defined as number of steps executed by algorithm on input. It is depend upon size of inputs, the running time should be independent.

$C:\Users\Kilua Zoldyck\Pictures\aa.png$

Algorithm - An algorithm is any well-defined computational procedure that takes some values or set of values as input and produces some values or set of values as output.

Logic: - Logic requires accurate identification of facts, elimination of cognitive error, and drawing of reasonable conclusions.

Data structure Data structure could also be a representation of the logical relationship existing between individual elements of knowledge.

Q7 How to find complexity using step count method

Step-count Method and Asymptotic Notation

In this section, we shall check out analysis of algorithms using step count method. Time and spacecomplexity are calculated using step count method.

Some basic assumptions are;

{ There is no count for f and g .
{ Each basic statement like 'assignment' and 'return' have a count of 1.
{ If a basic statement is iterated, then multiply by the amount of times the loop is run.
{ The loop statement is iterated n times, it's a count of (n + 1). Here the loop runs n times
for truth case and a check is performed for the loop exit (the false condition),hence the additional 1 in the count.

Example

1. Sum of elements in an array

Sno	Algorithm	Step count (time)	Step count (space)
1	Algorithm SUM(a,n)	0
2	sum = 0;	1	1 word for sum
3	for i = 1 to n do	n+1	1 word each for i and n
4	sum = sum + a[i];	n	n words for the array a[]
5	return sum	1
6	}	0

Total: (2n+3) (n+3) words

2.Adding two matrices of order m and n

S no	Algorithm	Step count	Step count
1	Algorithm Add(a, b, c, m, n)	------------
2	{	------------
3	for i = 1 to m do	------------	m +1
4	for j = 1 to n do	------------	m(n+1
5	c[i,j] = a[i,j] + b[i,j]	------------	m.n
6	}	------------

Total no of steps= 2mn + 2m + 2

Q8What are the basic algorithmic programming construct?

Analysis of programming constructs

1. Constant-Time Algorithms - O(1)

A constant-time algorithm is one that takes an equivalent amount of your time, no matter its input.

2. Logarithmic-Time Algorithm - O(log n)

A logarithmic-time algorithm is one that needs variety of steps proportional to the log(n). In most cases, we use 2 because the base of the log, but it doesn't matter which base because we ignore constants. Because we use the bottom 2, we will rephrase this within the following way: whenever the dimensions of the input doubles, our algorithm performs another step

3. Linear-Time Algorithms - O(n)

A linear-time algorithm is one that takes variety of steps directly proportional to the dimensions of the input. In other words, if the dimensions of the input doubles,then the amount of steps doubles.

4. Quadratic-Time Algorithms - O(n2)

Quadratic-time algorithm is one that takes variety of steps proportional to n2. That is, if the dimensions of the input doubles, then the amount of steps quadruples. A typical pattern of quadratic time algorithms is performing a linear-time operation on each item of the input (n steps per item * n items = n2 steps).

5. Cubic-Time Algorithms - O(n3)

Cubic-time algorithm is one that takes variety of steps proportional to n3. In other words, if the input doubles, the amount of steps is multiplied by 8. Similarly to the quadratic case, this might be the results of applying an n2 algorithm to n items or applying a linear algorithm to n2 items.

6. Exponential-Time Algorithms - O(2n)

An exponential-time algorithm is one that takes time proportional to 2n. In other words, if the dimensions of the input increases by one, the amount of steps doubles. Note that logarithms and exponents are inverses of every other. Algorithms during this category are often considered too slow to be practical, especially if the input is usually large.

S no	Constructs	Complexity
1	Constant	O(1)
2	Logarithmic	O(log n)
3	Linear	O(n)
4	Quadratic	O(n2)
5	Cubic	O(n3)
6	exponential	O(2n)

Q9 Explain types of data structures?

Abstract data types

• Abstract Data type (ADT) may be a type (or class) for objects whose behavior is defined by a group useful and a group of operations.

• The definition of ADT only mentions what operations are to be performed but not how these operations are going to be implemented.

• It doesn't specify how data are going to be organized in memory and what algorithms are going to be used for implementing the operations.

• It’s called “abstract” because it gives an implementation-independent view.

• The method of providing only the essentials and hiding the small print is understood as abstraction.

• The user of knowledge type doesn't got to skills that data type is implemented, for instance , we've been using Primitive values like int, float, char data types only with the knowledge that these data type can operate and be performed on with none idea of how they're implemented. So a user only must know what a knowledge type can do, but not how it'll be implemented. Consider

ADT as a recorder which hides the inner structure and style of the info type

1. Primitive data structures

• Primitive data structures are basic structures and are directly operated upon by machine instructions.

• Primitive data structures are represented different in different computers.

• Integers, floats, character and pointers are samples of primitive data structures.

• These data types are available in most programming languages as inbuilt type.

Integer: it is a knowledge type which allows all values without fraction part. We will use it for whole numbers.

Float: it is a knowledge type which use for storing fractional numbers.

Character: it is a knowledge type which is used for character values.

Pointer: pointer is a variable that holds memory address of another variable. Represented by *p.

Non primitive Data Type

• These are more sophisticated data structures.

• These are derived from primitive data structures.

• The non-primitive data structures emphasize on structuring of a gaggle of homogeneous or heterogeneous data items.

• Some of Non-primitive data types are Array, List, and File.

• A Non-primitive data type is further divided into Linear and Non-Linear arrangement

• Array: An array could also be a fixed-size sequenced collection of elements of the same data type.

• List: An ordered set containing variable number of elements is known as Lists.

• File: A file may be a collection of logically related information. It are often viewed as an outsized list of records consisting of varied fields.

Static data structure

Static arrangement memory size is fixed whereas in Dynamic arrangement, the dimensions are often randomly updated during run time which can be considered efficient with reference to memory complexity of the code.

Static arrangement provides more easier access to elements with reference to dynamic arrangement

Dynamic data structure

In competitive programming the constraints on memory limit isn't much high and that we cannot exceed the memory limit.

Given higher value of the constraints we cannot allocate a static arrangement of that size so Dynamic Data Structures are often useful.

Ephemeral data structure- An ephemeral data structure is one for which only one version is available at a time: after an update operation, the structure as it existed before the update is lost.

Persistent Data Structure- A persistent structure is one where multiple versions are simultaneously accessible: after an update, both old and new versions are often used

Q10 What are the types of algorithm and how to analyze an algorithm.

Types of Algorithm

There are two ways to write an algorithm, namely, top-down approach (Iterative algorithm) andbottom-up approach (Recursive algorithm). For example, the iterative and recursive algorithm for finding a factorial of a given number n is given below:

1. Iterative : means repetitive

Fact(n)

{

For i = 1 to n

fact = fact * i;

return fact;

}

Here the factorial is calculated as 1 * 2 * 3 * : : : * n.

2. Recursive : calls itself

Fact(n)

{

if n = 1

return 1;

else

return n * fact(n-1);

}

Here the factorial is calculated as n * (n - 1) *: : : * 1.

2 Algorithm: Analysis

The analysis of algorithms involves the following measures and are listed in the order of priority.

1. Correctness: For any algorithm, a proof of correctness is important which will exhibit thefact that the algorithm indeed output the desired answer. Often, discovering the underlying combinatorics is quite challenging.

2. Amount of work done (time complexity): For a problem, there may exist many algorithms. Comparison of two algorithms is inevitable to pick the best of two. By analysis we mean, the amount of time and space required to execute the algorithm. A computational problem canhave many algorithms but the estimation of time and space complexity provide an insight intoreasonable directions of search for finding the efficient algorithm. The time Complexity doesnot refer to the actual running time of an algorithm in terms of millisec (system time). Theactual running time depends on the system configuration. An algorithm taking 100_s on Intelmachine may take 10_s on an AMD machine. So, the time complexity must be depended independent of the system configuration. For each algorithm, we focus on step count: the numberof times each statement in the algorithm is executed, which in some sense reflects thetime complexity. The step count focuses on primitive operations along with basic operations.

Moreover, this number increases with the problem size. Therefore, we express the step count (time complexity) as a function of the input size. The notion input size and primitive operationsvary from one problem to another. The popular ones are;

3. Note: The number of primitive operations increases with the problem size. Therefore, we express the step count (time complexity) as a function of the input size. Space complexity is a relatedcomplexity measure that refers to the amount of space used by an algorithm. Here again, the analysis focuses on the number of words required leaving the system details. It is goodto highlight that this measure is considered less significant compared to the time complexityanalysis.

4. Optimality: For a given combinatorial problem, there may exist many algorithms. A natural question is to find the best algorithm (efficient), i.e., one might be interested in discovering bestever possible. This study also helps us to understand the inherent complexity of the problem.

Sign Up