UNIT 2
QUESTIONS
Q1 What is array and its advantages?
Array
Element: Every item stored in an array is termed as a component
Index: each memory location of a component in an array is denoted by a numerical index which is used for identifying the element
The array could also be a fixed-size sequenced collection of variables belonging to the same data types. The array has adjacent memory locations to store values. Since the array provides a convenient structure for representing data, it falls under the category of the data structures in C.
The syntax for declaring array are:
data_typearray_name [array_size];
• An array may be a container of elements.
• Elements have a selected value and data type, like "ABC", TRUE or FALSE, etc.
• Each element also has its own index, which is employed to access the element.
• Elements are stored at contiguous memory locations.
• An index is usually but the entire number of array items.
• In terms of syntax, any variable that's declared as an array can store multiple values.
• Most languages have an equivalent comprehension of arrays but have alternative ways of declaring and initializing them.
Three parts will always remain common altogether the initializations, i.e., array name, elements, and thus the info kind of elements.
• Array name: necessary for straightforward regard to the gathering of elements
• Data Type: necessary for type checking and data integrity
• Elements: these are the info values present in an array
Why can we need arrays?
• Here, are some reasons for using arrays:
Basic operations in array
There is some specific operation which can be performed or people that are supported by the array. These are:
• Traversing: It prints all the array elements one after another.
• Inserting: It adds a component at given index.
• Deleting: it's wont to delete a component at given index.
• Searching: It searches for an element(s) using given index or by value.
• Updating: it's wont to update a component at given index
Advantages and drawbacks of Arrays
Advantages
1. Reading an array element is simple and efficient. As shown within the above table, the read time of array is O(1) in both best and worst cases. This is often because any element are often instantly read using indexes (base address calculation behind the scene) without traversing the whole array.
2. Array could also be a foundation of other data structures. For instance other data structures like LinkedList, Stack, Queue etc. are implemented using array.
3. All the weather of an array are often accessed employing one name (array name) in conjunction with the index, which is readable, user-friendly and efficient rather than storing those elements in different-2 variables.
Disadvantages
1. While using array, we must need to make the selection of the size of the array within the start, so if we aren't aware what percentage elements we are becoming to store in array, it'd make the task difficult.
2. The size of the array is fixed so if at later point, if we'd wish to store more elements in it then it can’t be done. On the other hand, if we store less number of elements than the declared size, the remaining allocated memory is wasted.
Q2 Write a c program for merging 2 arrays?
C program to merge 2 arrays
C program to merge two sorted arrays
// It is assumed a user will enter arrays in ascending order
#include <stdio.h>
void merge(int [], int, int [], int, int []);
int main() {
int a[100], b[100], m, n, c, sorted[200];
printf("Input number of elements in first array\n");
scanf("%d", &m);
printf("Input %d integers\n", m);
for (c = 0; c < m; c++) {
scanf("%d", &a[c]);
}
printf("Input number of elements in second array\n");
scanf("%d", &n);
printf("Input %d integers\n", n);
for (c = 0; c < n; c++) {
scanf("%d", &b[c]);
}
merge(a, m, b, n, sorted);
printf("Sorted array:\n");
for (c = 0; c < m + n; c++) {
printf("%d\n", sorted[c]);
}
return 0;
}
void merge(int a[], int m, int b[], int n, int sorted[]) {
inti, j, k;
j = k = 0;
for (i = 0; i< m + n;) {
if (j < m && k < n) {
if (a[j] < b[k]) {
sorted[i] = a[j];
j++;
}
else {
sorted[i] = b[k];
k++;
}
i++;
}
else if (j == m) {
for (; i< m + n;) {
sorted[i] = b[k];
k++;
i++;
}
}
else {
for (; i< m + n;) {
sorted[i] = a[j];
j++;
i++;
}
}
}
}
Q3 Write a program for polynomial addition
Polynomial addition
Consider below program to understand addition of two polynomial
#include<stdio.h>
#include<math.h>
/*
This structure is used to store a polynomial term. An array of such terms represents a polynomial.
The "coeff" element stores the coefficient of a term in the polynomial, while the "exp" element stores the exponent.
*/
struct poly
{
floatcoeff;
intexp;
};
//declaration of polynomials
struct poly a[50],b[50],c[50],d[50];
int main()
{
inti;
int deg1,deg2; //stores degrees of the polynomial
int k=0,l=0,m=0;
printf("Enter the highest degree of polynomial1:");
scanf("%d",°1); //taking polynomial terms from the user
for(i=0;i<=deg1;i++)
{
//entering values in coefficient of the polynomial terms
printf("\nEnter the coeff of x^%d :",i);
scanf("%f",&a[i].coeff);
//entering values in exponent of the polynomial terms
a[k++].exp = i;
}
//taking second polynomial from the user
printf("\nEnter the highest degree of polynomial2:");
scanf("%d",°2);
for(i=0;i<=deg2;i++)
{
printf("\nEnter the coeff of x^%d :",i);
scanf("%f",&b[i].coeff);
b[l++].exp = i;
}
//printing first polynomial
printf("\nExpression 1 = %.1f",a[0].coeff);
for(i=1;i<=deg1;i++)
{
printf("+ %.1fx^%d",a[i].coeff,a[i].exp);
}
//printing second polynomial
printf("\nExpression 2 = %.1f",b[0].coeff);
for(i=1;i<=deg2;i++)
{
printf("+ %.1fx^%d",b[i].coeff,b[i].exp);
}
//Adding the polynomials
if(deg1>deg2)
{
for(i=0;i<=deg2;i++)
{
c[m].coeff = a[i].coeff + b[i].coeff; c[m].exp = a[i].exp;
m++;
}
for(i=deg2+1;i<=deg1;i++)
{
c[m].coeff = a[i].coeff;
c[m].exp = a[i].exp;
m++;
}
}
else
{
for(i=0;i<=deg1;i++)
{
c[m].coeff = a[i].coeff + b[i].coeff;
c[m].exp = a[i].exp;
m++;
}
for(i=deg1+1;i<=deg2;i++)
{
c[m].coeff = b[i].coeff;
c[m].exp = b[i].exp;
m++;
}
}
//printing the sum of the two polynomials
printf("\nExpression after addition = %.1f",c[0].coeff);
for(i=1;i<m;i++)
{
printf("+ %.1fx^%d",c[i].coeff,c[i].exp);
}
return 0;
}
Output
Enter the highest degree of polynomial1:3
Enter the coeff of x^0:2
Enter the coeff of x^1:3
Enter the coeff of x^2:5
Enter the coeff of x^3 :1
Enter the highest degree of polynomial2:2
Enter the coeff of x^0 :7
Enter the coeff of x^1 :8
Enter the coeff of x^2 :5
Expression 1 = 2.0+ 3.0x^1+ 5.0x^2+ 1.0x^3
Expression 2 = 7.0+ 8.0x^1+ 5.0x^2
Expression after addition = 9.0+ 11.0x^1+ 10.0x^2+ 1.0x^3
Q4 Write aprogram for polynomial multiplication
Multiplication of Two Polynomial
#include<stdio.h>
#include<math.h>
/* This structure is used to store a polynomial term. An array of such terms represents a polynomial.
The "coeff" element stores the coefficient of a term in the polynomial, while the "exp" element stores the exponent.
*/
struct poly
{
floatcoeff;
intexp;
};
//declaration of polynomials
struct poly a[50],b[50],c[50],d[50];
int main()
{
inti;
int deg1,deg2; //stores degrees of the polynomial
int k=0,l=0,m=0;
printf("Enter the highest degree of polynomial1:");
scanf("%d",°1); //taking polynomial terms from the user
for(i=0;i<=deg1;i++)
{
//entering values in coefficient of the polynomial terms
printf("\nEnter the coeff of x^%d :",i);
scanf("%f",&a[i].coeff); //entering values in exponent of the polynomial terms
a[k++].exp = i;
}
//taking second polynomial from the user
printf("\nEnter the highest degree of polynomial2:");
scanf("%d",°2);
for(i=0;i<=deg2;i++)
{
printf("\nEnter the coeff of x^%d :",i);
scanf("%f",&b[i].coeff);
b[l++].exp = i;
}
//printing first polynomial
printf("\nExpression 1 = %.1f",a[0].coeff);
for(i=1;i<=deg1;i++)
{
printf("+ %.1fx^%d",a[i].coeff,a[i].exp);
}
//printing second polynomial
printf("\nExpression 2 = %.1f",b[0].coeff);
for(i=1;i<=deg2;i++)
{
printf("+ %.1fx^%d",b[i].coeff,b[i].exp);
}
//Multiply the polynomials
if(deg1>deg2)
{
for(i=0;i<=deg2;i++)
{
c[m].coeff = a[i].coeff * b[i].coeff;
c[m].exp = a[i].exp;
m++;
}
for(i=deg2+1;i<=deg1;i++)
{
c[m].coeff = a[i].coeff;
c[m].exp = a[i].exp;
m++;
}
}
else
{
for(i=0;i<=deg1;i++)
{
c[m].coeff = a[i].coeff * b[i].coeff;
c[m].exp = a[i].exp;
m++;
}
for(i=deg1+1;i<=deg2;i++)
{
c[m].coeff = b[i].coeff;
c[m].exp = b[i].exp;
m++;
}
}
//printing the product of the two polynomials
printf("\nExpression after multiplication = %.1f",c[0].coeff);
for(i=1;i<m;i++)
{
printf("+ %.1fx^%d",c[i].coeff,c[i].exp);
}
return 0;
}
On compiling and executing above program, following is the output produced on my computer
Enter the highest degree of polynomial1:2
Enter the coeff of x^0 :2
Enter the coeff of x^1 :3
Enter the coeff of x^2 :4
Enter the highest degree of polynomial2:3
Enter the coeff of x^0 :5
Enter the coeff of x^1 :6
Enter the coeff of x^2 :7
Enter the coeff of x^3 :2
Expression 1 = 2.0+ 3.0x^1+ 4.0x^2
Expression 2 = 5.0+ 6.0x^1+ 7.0x^2+ 2.0x^3
Expression after multiplication = 10.0+ 18.0x^1+ 28.0x^2+ 2.0x^3
Q5 What is Sparse matrix, Explain?
Sparse matrix
• An mXn matrix is claimed to be sparse if “many” of its elements are zero.
• A matrix that is not sparse is called a dense matrix.
• We can device a simple representation scheme whose space requirement equals the size of the nonzero elements.
Example:-
• The non-zero entries of a sparse matrix could also be mapped into a linear list in row-major order.
• for instance the non-zero entries of 4X8 matrix of below
• in row major order are 2, 1, 6, 7,3, 9, 8, 4, 5
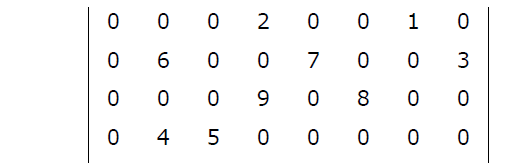
Figure A 4 x 4 matrix

Figure Linear Representation of above matrix
• To construct matrix structure we need to record
(a) Original row and columns of every non zero entries
(b) No of rows and columns within the matrix
• So each element of the array into which the sparse matrix is mapped need to have three fields: row, column and value
• A corresponding amount of time is saved creating the linear list representation over initialization of two dimension array.
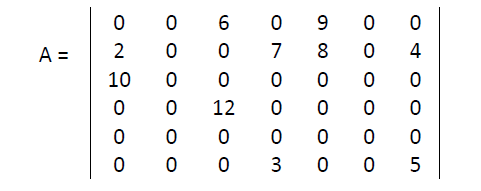
• Here from 6X7=42 elements, only 10 are non zero. A[1,3]=6, A[1,5]=9, A[2,1]=2, A[2,4]=7, A[2,5]=8, A[2,7]=4, A[3,1]=10, A[4,3]=12, A[6,4]=3, A[6,7]=5.
• One basic method for storing such a sparse matrix is to store non-zero elements in one dimensional array and to spot each array elements with row and column indices
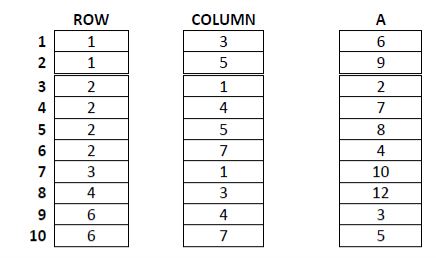
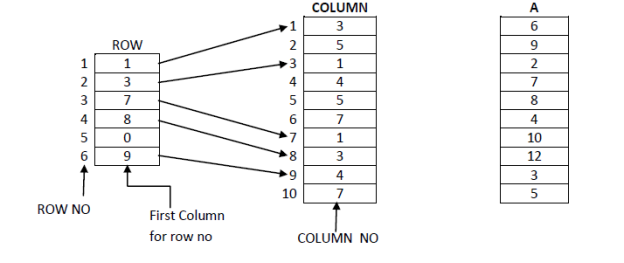
• A more efficient representation in terms of storage requirement and access time to the row of the matrix is shown in fid (d). The row vector changed in order that its ith element is that the index to the primary of the column indices for the element in row I of the matrix.
Linked Representation of Sparse matrix
Typical node to represent non-zero element is
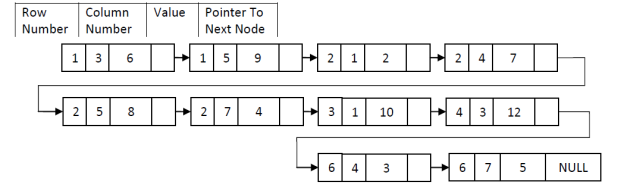
Figure:-linked representation of sparse matrix
Q6 Explain ordered data types and how it differ from arrays?
Ordered list
• The structure of an ordered list is a collection of items where each item holds a relative position that is based upon some underlying characteristic of the item.
• The ordering is typically either ascending or descending and we assume that list items have a meaningful comparison operation that is already defined.
• Many of the ordered list operations are the same as those of the unordered list.
• OrderedList() creates a new empty ordered list. It doesn’t require any parameters and returns an empty list.
• add(item) adds a new item to the list making sure that the order is preserved. It needs the item and returns nothing. Assume the item is not already in the list.
• remove(item) removes the item from the list. It needs the item and modifies the list. Assume the item is present in the list.
• search(item) searches for the item in the list. It needs the item and returns a boolean value.
• isEmpty() tests to see whether the list is empty. It needs no parameters and returns a boolean value.
• size() returns the number of items in the list. It needs no parameters and returns an integer.
• index(item) returns the position of item in the list. It needs the item and returns the index. Assume the item is in the list.
• pop() removes and returns the last item in the list. It needs nothing and returns an item. Assume the list has at least one item.
• pop(pos) removes and returns the item at position pos. It needs the position and returns the item. Assume the item is in the list.
Array and ordered list
S no | Array | Ordered list |
1 | An array is a contiguous segment of memory, and a list is just a bunch of nodes, each one has the pointers to the "next" node (and also to the "previous" node, in the case of bidirectional lists). | The structure of an ordered list is a collection of items where each item holds a relative position that is based upon some underlying characteristic of the item. The ordering is typically either ascending or descending and we assume that list items have a meaningful comparison operation that is already defined. |
2 | Arrays efficiently - in O(1) - support random access (i.e. by arbitrary given index i), | Lists, on the other hand, do not support efficient random access (while supporting efficient consecutive traversal) |
3 | Deleting/inserting an element into an array is slow - O(n), because you have to move all elements after deleting/inserting element | Inserting and deleting is fast - O(1). |
4 | In the array, you have to shuffle other entries around; in a list, you simply adjust appropriate pointers in at most 3 elements | it is possible to add items to a particular point in the list more swiftly than it is possible to add a new item in an array at an equivalent point |
5 | Access to the Nth item takeO(1) time for an array. | Access to the Nth item in a list takes O(N) time |
6 | The items in an array are not necessarily in any particular order | The items in a list are always arranged in any particular order |
7 | With arrays, you can do random access of a member in O(1), while this takes O(N) in an list.
| Performance wise, maintaining an ordered list is pretty expensive: O(N) insert, delete, but you can do searches faster than O(N) (using something like binary search) |
Q7 How 2 polynomials can be added in array?
A polynomial could also be represented using array or structure. A structure could also be defined such it contains two parts – one is that the coefficient and second is that the corresponding exponent. The structure definition could also be given as shown below:
Structpolynomial{
int coefficient;
int exponent;
};
Algorithm: adding polynomial using structures
AddPoly(Struct Poly p1[10], Struct Poly p2[10], int t1,int t2,Struct Poly p3[10])
[Initialize Counter] Set i=0,j=0,k=0
2. Repeat step 3 while i<t1 and j<t2
If p1[i].expo=p2[j].expo, then
3. p3[i].coeff=p1[i].coeff+p2[i].coeff
p3[k].expo=p1[i].expo
[Increase counter] Set i=i+1,j=j+1,k=k+1
else if p1[i].expo > p2[j].expo, then
p3[k].coeff=p1[i].coeff
p3[k].expo=p1[i].expo
[Increase counter] Set i=i+1,k=k+1
else
p3[k].coeff=p2[j].coeff
p3[k].expo=p2[j].expo
Set j=j+1,k=k+1
[End of If]
[End of loop]
4. Repeat while i<t1
p3[k].coeff=p1[i].coeff
p3[k].expo=p1[i].expo
Set i=i+1,k=k+1
[End of loop]
5. Repeat while j<t2
p3[k].coeff=p2[j].coeff
p3[k].expo=p2[j].expo
Set j=j+1,k=k+1
[End of loop]
6. Return k
7. Exit
Adding polynomial using array
Addition of polynomial is easy as compared to multiplication
add (A[0..m-1], B[0..n01])
1) Create a sum array sum[] of size equal to maximum of 'm' and 'n'
2) Copy A[] to sum[].
3) Traverse array B[] and do following for every element B[i]
4) sum[i] = sum[i] + B[i]
5) Return sum[].
Example :-
Input: A [] = {5, 0, 10, 6} similar to Pa =6x3+10x2+5
B [] = {1, 2, 4} similar to Pb =4x2+2x+1
Output: sum [] = {6, 2, 14, 6} similar to Psum= 6x3+14x2+2x+6
Q8 Explain transpose and multiplication of sparse matrix
Transpose of sparse matrix
Algorithm for Transpose of Sparse Matrix
SparseMatrixSparseMatrix::Transpose()
{
Construct a SparseMatrix, b(cols, rows, terms);
If (terms > 0)
{
Let rowSize be an integer array of size cols.
Let rowStart be an integer array of size cols.
Initialize each element in rowSize to 0.
For (i=0; i
rowSize [smArray[i].col]++;
rowStart [0] = 0;
For (i = 1; i< cols; i++)
rowStart [i] = rowSize [i-1] + rowStart [i-1];
For (i=0; i< terms; i++) {
j = rowStart [ smArray [i].col ];
Copy smArray[ i ] to smArray[ j ];
Interchange row and col of smArray[ j ];
rowStart [ smArray [i].col ]++;
}
}
Return b;
}
Multiplication of sparse matrix
Multiplying Sparse Matrices
1 void mm_mul_sa (sa_t *A, sa_t *B, sa_t *C)
2 {
3 inti, j, k;
4 int sum;
5
6 for (i = 0; i< A->num_rows; i++) {
7 for (j = 0; j < B->num_cols; j++) {
8 sum = 0;
9 for (k = 0; k < A->num_cols; k++) {
10 sum += saGet (A,i,k) * saGet (B,k,j);
11 }
12 saSet (C,i,j,sum);
13 }
14 }
15 }
Q9 How an address of array is stored in row major and column major array operations?
An array can be stored in many ways
Array A= [ a11 a12 a13 ]
[ a21 a22 a23 ]
Array could be stored in possible ways
Index | Row major | Column major |
0 | A11 | A11 |
1 | A12 | A21 |
2 | A13 | A12 |
3 | A21 | A22 |
4 | A22 | A13 |
5 | A23 | A23 |
Different programming languages handles array in different ways.
• In C programming , multidimensional arrays are stored in row-major order, and the array indexes are written row-first (lexicographical access order):
C: row-major order (lexicographical access order), zero-based indexing
Index | Value | Access |
0 | A11 | A[0][0] |
1 | A12 | A[0][1] |
2 | A13 | A[0][2] |
3 | A21 | A[1][0] |
4 | A22 | A[1][1] |
5 | A23 | A[1][2] |
• Address of [I, J]th element in row-major = B + W[C(I – Kr) + (J – Kc)]
• In Fortran, arrays are stored in column-major order, while the array indexes are still written row-first (colexicographical access order):
Fortran: column-major order (colexographical access order), one-based indexing
Index | Value | Access |
1 | A11 | A[1][1] |
2 | A21 | A[2][1] |
3 | A12 | A[1][2] |
4 | A22 | A[2][2] |
5 | A13 | A[1][3] |
6 | A23 | A[2][3] |
• Address of [I, J]th element in column-major = B + W[R(J – Kc) + (I – Kr)]
• Where :
• B is the base address (address of the first block in the array).
• W is the width in bytes (size in bytes for each block in the array).
• Kr is the index of the first row.
• Kc is the index of the first column.
• R is the total number of rows.
• C is the total number of columns.
Q10 Explain how 2 polynomials can be added using array
Multiplication of Two Polynomial
Multiplication of two polynomials however requires manipulation of each node such that the exponents are added up and the coefficients are multiplied. After each term of first polynomial is operated upon with each term of the second polynomial, then the result has to be added up by comparing the exponents and adding the coefficients for similar exponents and including terms as such with dissimilar exponents in the result
Algorithm:
multiply(A[0..m-1], B[0..n01])
1) Create a product array prod[] of size m+n-1.
2) Initialize all entries in prod[] as 0
3) Traverse array A[] and do following for every element A[i]
4) Return prod[].
A simple solution is to one by one consider every term of first polynomial and multiply it with every term of second polynomial.
Example:-
Input: A [] = {5, 0, 10, 6} similar to Pa =6x3+10x2+5
B [] = {1, 2, 4} similar to Pb =4x2+2x+1
Output: prod [] = {5, 10, 30, 26, 52, 24}
Similar to Pmul= 24x5+52x4+26x3+30x2+10x+5
p1=4x2+3x+2
p2=2x3+7x2+6x+5
pmul= 2x3+28x2+18x+10
Enter the highest degree of polynomial1= 2
Enter the coeff of x^0 = 2
Enter the coeff of x^1 = 3
Enter thecoeff of x^2 =4
Enter the highest degree of polynomial 2 = 3
Enter the coeff of x^0 = 5
Enter the coeff of x^1 = 6
Enter the coeff of x^2 = 7
Enter the coeff of x^3 = 2
Expression 1 = 2.0+ 3.0x^1+ 4.0x^2
Expression 2 = 5.0+ 6.0x^1+ 7.0x^2+ 2.0x^3
Expression after multiplication = 10.0+ 18.0x^1+ 28.0x^2+ 2.0x^3