undefined | unit 4 linked list

FDS

UNIT 4

QUESTIONS

Q1 What is link list and write its advantages and disadvantages

The linked allocation method of storage may result in both efficient use of memory and computer time.

A linked list may be a non-sequential collection of knowledge items.

The concept of a linked list is extremely simple, for each data item within the linked list, there's an associated pointer that might give the memory allocation of subsequent data item within the linked list.

The data items within the linked list aren't during a consecutive memory locations but they'll be anywhere in memory.

Accessing of those data items is simpler as each data item contains within itself the address of subsequent data item.

Linked List

A linked list may be a collection of objects stored during a list form.

A linked list may be a sequence of things (objects) where every item is linked to subsequent.

A linked list may be a non-primitive sort of arrangement during which each element is dynamically allocated and during which elements point to every other to define a linear relationship

Elements of linked list are called nodes where each node contains two things, data and pointer to next node.

Linked list require more memory compared to array because alongside value it stores pointer to next node.

Linked lists are among the only and commonest data structures. They will be wont to implement other data structures like stacks, queues, and symbolic expressions, etc…

Operations on linked list

Insert

Insert initially position

Insert eventually position

Insert into ordered list

Delete

Traverse list (Print list)

Copy linked list

Advantages of Linked List

Linked lists are dynamic data structures: that's, they will grow or shrink during execution of a program.

Efficient memory utilization: Here memory isn't pre-allocated. Memory is allocated whenever it’s required. And it's deallocated (free) when it's not needed.

Insertion and deletions are easier and efficient: Linked list provide flexibility in inserting a knowledge item at a specified position and deletion of a knowledge item from the given position.

Elements of linked list are flexible: It are often primary data type or user defined data types

Disadvantages of Linked List

Random access isn't allowed. We've to access elements sequentially ranging from the primary node.

Basically we can’t perform binary search with linked lists.

It can't be easily sorted

We must traverse 1/2 the list on the average to access any element

More complex to make than an array

Extra memory space for a pointer is required with each element of the list

Q2What are types of linked list

Types of linked list

1. Singly Linked List

It is basic sort of linked list.

Each node contains data and pointer to next node.

Last node’s pointer is null.

Limitation of singly linked list is we will traverse only in one direction, forward direction.

$C:\Users\Kilua Zoldyck\Pictures\3.png$

2. Circular Linked List

Circular linked list may be a singly linked list where last node points to first node within the list.

It doesn't contain null pointers like singly linked list.

We can traverse only in one direction that's forward direction.

It has the most important advantage of your time saving once we want to travel from last node to first node, it directly points to first node.

An honest example of an application where circular linked list should be used may be a timesharing problem solved by the OS.

$C:\Users\Kilua Zoldyck\Pictures\2.png$

3. Doubly Linked list

Each node of doubly linked list contains data and two tips that could point previous (LPTR) and next (RPTR) node.

Main advantage of doubly linked list is we will traverse in any direction, forward or reverse.

Other advantage of doubly linked list is we will delete a node with little trouble, since we've pointers to the previous and next nodes. A node on a singly linked list can't be removed unless we have the pointer to its predecessor.

Drawback of doubly linked list is it requires more memory compared to singly linked list because we need an additional pointer to point previous node.

L and R in image denote left most and right most nodes within the list.

Left link of L node and right link of R node is NULL, indicating the top of list for every direction.

$C:\Users\Kilua Zoldyck\Pictures\4.png$

4. Doubly circular link list

Circular Doubly Linked List has properties of both doubly linked list and circular linked list during which two consecutive elements are linked or connected by previous and next pointer and therefore the last node points to first node by next pointer and also the primary node points to last node by previous pointer.

$C:\Users\Kilua Zoldyck\Pictures\1.png$

Q3 Write basic operations in linked list

1. Singly linked list

1. Insertion at start first position

Function: INSERT(X, First)

Given X may be a replacement element and FIRST may be a pointer to the primary element of a linked linear list. Typical node containsINFO and LINK fields.

AVAIL may be a pointer to the highest element of the supply stack; NEW may be a temporary pointervariable.

This function inserts a replacement node at the primary position of linked list.

This function returns address ofFIRST node.

[Underflow?]
IF AVAIL = NULL
Then Write (“Availability Stack Underflow”)
Return(FIRST)

[Obtain address of next free Node]
AVAIL←NEW

[Remove free node from Availability Stack]
LINK(AVAIL)←AVAIL

[Initialize fields of latest node and its link to the list]
X←INFO (NEW)
FIRST←LINK (NEW)

[Return address of latest node]
Return (NEW)
When INSERT is invoked it returns a pointer value to the variable FIRST
INSERT (X, FIRST)←FIRST

2. Insertion at end

Function: INSEND(X, First) (Insert at end)

Given X, a replacement element and FIRST may be a pointer to the primary element of a linked linear list. Typical node contains
INFO and LINK fields.

AVAIL may be a pointer to the highest element of the supply stack; NEW may be a temporary pointer
variable.

This function inserts a replacement node at the last position of linked list.

This function returns address of FIRSTnode.

[Underflow?]
IF AVAIL = NULL
Then Write (“Availability Stack Underflow”)
Return(FIRST)

[Obtain address of next free Node]
AVAIL←NEW

[Remove free node from Availability Stack]
LINK(AVAIL)←AVAIL

[Initialize field of latest node]
X←INFO (NEW)
NULL←LINK (NEW)

[Is the list empty?]
If FIRST = NULL
then Return (NEW)

[Initialize look for a final node]
FIRST←SAVE

[Search for end of list]
Repeat while LINK (SAVE) ≠ NULL
LINK (SAVE)←SAVE

[Set link field of last node to NEW)
NEW←LINK (SAVE)

[Return first node pointer]
Return (FIRST)
When INSERTEND is invoked it returns a pointer value to the variable FIRST
INSERTEND (X, FIRST)←FIRST

3. Deletion a node from Linked List

If a linked list is empty, then write under flow and return.

Repeat step 3 while end of the list has not been reached and therefore the node has not been found.

Obtain subsequent node in list and record its predecessor node.

If the top of the list has been reached then write node not found and return.

Delete the node from list.

Return the node into availability area.

Function: DELETE(X, FIRST)

Given X, an address of node which we would like to delete and FIRST may be a pointer to the primary element of a linked linearlist.

Typical node contains INFO and LINK fields. SAVE &PRED are temporary pointer variables.

[Is Empty list?]
If FIRST = NULL
then write (‘Underflow’)
return

[Initialize look for X]
FIRST←SAVE

[Find X]
Repeat thru step-5 while SAVE ≠ X and LINK (SAVE) ≠ NULL

[Update predecessor marker]
SAVE←PRED

[Move to next node]
LINK (SAVE)←SAVE

[End of the list]
If SAVE ≠ X
then write (‘Node not found’)
return

[Delete X]
If X = FIRST (if X is first node?)
LINK (FIRST)←then FIRST
LINK (X)←else LINK (PRED)

[Free Deleted Node]
Free (X)

Q4 Write basic operations in doubly linked list

Doubly linked list

1. Insertion in first

Function: DOUBINS (L, R, M, X)

Given a doubly link list whose left most and right most nodes addressed are given by the pointer variables L and R respectively. It’s required to insert a node whose address is given by the pointer variable NEW. The left and right links of nodes are denoted by LPTR and RPTR respectively. The knowledge field of a node is denoted by variable INFO. The name of a component of the list is NODE. The insertion is to be performed to the left of a specific node with its address given by the pointer variable M. the knowledge to be entered within the node is contained in X.

[Create New Empty Node]

NEW NODE

2. [Copy information field]

INFO (NEW) ← X

3. [Insert into an empty list]

If R = NULL

Then LPTR (NEW) ←RPTR (NULL) ← NULL

L ← R ← NEW

Return

4. [Is left most insertion?]

If M = L

Then LPTR (NEW)←NULL

RPTR (NEW) ← M

LPTR (M)← NEW

L ← NEW

Return

5. [Insert in middle]

LPTR (NEW)←LPTR (M)

RPTR (NEW) ← M

LPTR (M) ← NEW

RPTR (LPTR (NEW)) ← NEW

6. Return

2. Insertion in middle

Function: DOUBINS_ORD (L, R, M, X)

Given a doubly link list whose left most and right most nodes addressed are given by the pointer variables L and R respectively. It’s required to insert a node whose address is given by the pointer variable NEW. The left and right links of nodes are denoted by LPTR and RPTR respectively. The knowledge field of a node is denoted by variable INFO. The name of a component of the list is NODE. The insertion is to be performed in ascending order of info part. The knowledge to be entered within the node is contained in X.

[Create New Empty Node]

NEW NODE

2. [ Copy information field]

INFO (NEW) ← X

3. [Insert into an empty list]

If R = NULL

Then LPTR (NEW) ←RPTR (NULL) ← NULL

L ← R ← NEW

Return

4. [Does the new node precedes all other nodes in List?]

If INFO(NEW) ≤ INFO(L)

Then RPTR (NEW) ← L

LPTR(NEW)← NULL

LPTR (L) ← NEW

L ← NEW

Return

5. [Initialize temporary Pointer]

SAVE ← L

6. [Search for predecessor of latest node]

Repeat while RPTR(SAVE) ≠ NULL and INFO(NEW) ≥ INFO(RPTR(SAVE))

SAVE ←RPTR (SAVE)

7. [Set link field of latest node and its predecessor]

RPTR (NEW) ←RPTR(SAVE)

LPTR (RPTR(SAVE))←NEW

RPTR (SAVE) ← NEW

LPTR (NEW) ← SAVE

If SAVE = R

Then RPTR(SAVE)←NEW

3. Deletion in doubly link list

Function: DOUBDEL (L, R, OLD)

Given a doubly linked list with the addresses of left most and right most nodes are given by the pointer variables L and R respectively. it's required to delete the node whose address is contained within the variable OLD. Node contains left and right links with names LPTR and RPTR respectively.

[Is underflow?]

If R=NULL

Then write (‘UNDERFLOW’)

return

2. 2. [Delete node]

If L = R (single node in list)

Then L ← R ← NULL

else If OLD = L (left most node)

Then L ←RPTR(L)

LPTR (L) ← NULL

else if OLD = R (right most)

Then R←LPTR (R)

RPTR (R) ← NULL

elseRPTR (LPTR (OLD)) ←RPTR (OLD)

LPTR (RPTR (OLD)) ←LPTR (OLD)

3. 3. [ FREE deleted node]

FREE (OLD)

Q5 Write basic operations in circular linked list

Circular link list

1. Insertion at start

PROCEDURE: CIRCULAR_LINK_INSERT_FIRST (X, FIRST, LAST)

FIRST and LAST are tips that could the primary and last element of a circular linked linear list respectively whose typical node contains INFO and LINK fields. NEW may be a temporary pointer variable. This procedure inserts value X at the first position of Circular linked linear list.

[Create New Empty Node]

NEW ← NODE

2. [Initialize fields of latest node and its link to the list]

INFO (NEW) ←X

If FIRST = NULL

Then LINK (NEW) ←NEW

FIRST ← LAST ←NEW

else LINK (NEW) ← FIRST

LINK (LAST)←NEW

FIRST ←NEW

Return

2. Insertion at end

PROCEDURE: CIR_LINK_INSERT_END (X, FIRST, LAST)

[Create New Empty Node]

NEW ←NODE

2. [Initialize fields of latest node and its link to the list]

If FIRST = NULL

Then LINK (NEW) ←NEW

FIRST ←LAST ← NEW

else LINK(NEW) ← FIRST

LINK(LAST) ← NEW

LAST ← NEW

Return

3. Insertion in between

PROCEDURE: CIR_LINK_INSERT_ORDER (X, FIRST, LAST)

FIRST and LAST are tips that could the primary and last element of a circular linked linear list respectively whose typical node contains INFO and LINK fields. NEW may be a temporary pointer variable. This procedure inserts value X such that linked list preserves the ordering of the terms in increasing order of their INFO field.

[Create New Empty Node]

NEW ← NODE

2. [Copy information content into new node

INFO (NEW) ← X

3. [Is Linked List is empty?]

If FIRST = NULL

Then LINK (NEW) ← NEW

FIRST ← LAST ← NEW

Return

4. Does new node precedes all other nodes in List?]

If INFO (NEW) ≤ INFO (FIRST)

Then LINK (NEW) ← FIRST

LINK (LAST) ← NEW

FIRST ← NEW

Return

5. [Initialize Temporary Pointer]

SAVE ← FIRST

6. [Search for Predecessor of latest node]

Repeat while SAVE ≠ LAST and INFO(NEW) ≥ INFO(LINK(SAVE))

SAVE ←LINK(SAVE)

7. [Set link field of latest node and its Predecessor]

LINK(NEW) ← LINK(SAVE)

LINK(SAVE) ← NEW

If SAVE = LAST

Then LAST ← NEW

8. [Finish]

Return

4. Deletion in circular link list

PROCEDURE: CIR_LINK_DELETE (X, FIRST, LAST)

FIRST and LAST are tips that could the primary and last element of a circular linked linear list respectively whose typical node contains INFO and LINK fields. SAVE &PRED are temporary pointer variables. This procedure deletes a node whose address is given by pointer variable X.

[Is Empty List?]

If FIRST = NULL

Then write (‘Linked List is Empty’)

Return

2. [Initialize look for X]

SAVE ← FIRST

3. [Find X]

Repeat thru step 5 while SAVE ≠ X and SAVE ≠ LAST

4. [Update predecessor marker]

PRED← SAVE

5. [Move to next node]

SAVE ← LINK (SAVE)

6. [End of Linked List]

If SAVE ≠ X

Then write(‘Node not found’)

return

7. [Delete X]

If X = FIRST

Then FIRST ← LINK (FIRST)

LINK (LAST) ← FIRST

else LINK (PRED) ← LINK(X)

If X = LAST

Then LAST ←PRED

8. [Free Deleted Node]

Free (X)

Q6 How dynamically a link list can be represented?

Linked lists are inherently dynamic data structures; they believe new and delete (or malloc and free) for his or her operation. Normally, dynamic memory management is provided by the C/C++ standard library, with help from the OS.

Rather than representing data contiguously next to every other within the memory, linked list employs the concept of nodes and pointers.

A node holds the info item within the particular memory block and a pointer links from one node to a different and references the memory address of subsequent and former nodes (in the case of doubly linked list)

Basic allocator functionality

1. malloc(n) –

A request for n bytes of contiguous memory.

The allocator should return a pointer to such a block, if it's one available, or a null pointer if it doesn't.

The block of memory should be marked as “in-use” within the allocators internal state. (Secure allocators might zero memory before giving it over, to make sure that existing data isn't “leaked”.)

2. free(p) –

An offer to release the memory pointed to by p.

The allocator should mark the memory employed by p as not in-use. (Error-checking allocators might fill the memory with a recognizable byte pattern in order that use-after-free errors are easy to detect.)

To malloc a block,

Search through the list for a block whose size is a minimum of as big as requested. Of these blocks, we've a choice on which one to use, determined by the allocation strategy:

First Fit: use the primary block within the list which inserts

Best Fit: use the block within the list whose size is closest to the requested size.

Use the most/least recently free-d block (LIFO, FIFO).

When a block is freed,

add it to the list. this will be wiped out several ways

Add to the front of the list. (When used with first-fit, this leads to LIFO-like behavior).

Add to the rear of the list. (FIFO

Insert it into the list in order that the list is usually ordered by address. this is often commonest , because the structure of the list mirrors the structure of the memory layout.

node* new_node(long value, node* next)

{

node* n = (node*) malloc(sizeof(node));

n->value = value;

n->next = next;

return n;

}

A list will be identified by a node*. Hence, new_node above is also a kind of push_front, adding a new node to the beginning of a list.

Inserting a value

To insert a value, we pass a pointer to the node before the location to insert at, as well as the value to be inserted. In C, we would do

node* insert(node* p, long value)

{

node* n = new_node(value, p->next);

p->next = n;

return n;

}

Removing a node

Similarly, to remove a node, we pass a pointer to the node before it.

void remove(node* p)

{

node* n = p->next;

if(p->next)

p->next = p->next->next;

free(n);

}

Q7 Explain insertion operation in circular link list, singly link list, and doubly linked list?

Insertion at Singly linked list

Function: INSERT(X, First)

Given X may be a replacement element and FIRST may be a pointer to the primary element of a linked linear list. Typical node containsINFO and LINK fields.

AVAIL may be a pointer to the highest element of the supply stack; NEW may be a temporary pointervariable.

This function inserts a replacement node at the primary position of linked list.

This function returns address ofFIRST node.

6. [Underflow?]
IF AVAIL = NULL
Then Write (“Availability Stack Underflow”)
Return(FIRST)

7. [Obtain address of next free Node]
AVAIL←NEW

8. [Remove free node from Availability Stack]
LINK(AVAIL)←AVAIL

9. [Initialize fields of latest node and its link to the list]
X←INFO (NEW)
FIRST←LINK (NEW)

10. [Return address of latest node]
Return (NEW)
When INSERT is invoked it returns a pointer value to the variable FIRST
INSERT (X, FIRST)←FIRST

Insertion in doubly link list

Function: DOUBINS (L, R, M, X)

Given a doubly link list whose left most and right most nodes addressed are given by the pointer variables L andR respectively. It's required to insert a node whose address is given by the pointer variable NEW. The left andright links of nodes are denoted by LPTR and RPTR respectively. The knowledge field of a node is denoted byvariable INFO. The name of a component of the list is NODE. The insertion is to be performed to the left of aspecific node with its address given by the pointer variable M. the knowledge to be entered within the node is contained in X.

7. [Create New Empty Node]

NEW NODE

8. [Copy information field]

INFO (NEW) ← X

9. [Insert into an empty list]

If R = NULL

Then LPTR (NEW) ←RPTR (NULL) ← NULL

L ← R ← NEW

Return

10. [Is left most insertion?]

If M = L

Then LPTR (NEW)←NULL

RPTR (NEW) ← M

LPTR (M)← NEW

L ← NEW

Return

11. [Insert in middle]

LPTR (NEW)←LPTR (M)

RPTR (NEW) ← M

LPTR (M) ← NEW

RPTR (LPTR (NEW)) ← NEW

12. Return

Insertion at Circular link list

PROCEDURE: CIRCULAR_LINK_INSERT_FIRST (X, FIRST, LAST)

3. [Create New Empty Node]

NEW ← NODE

4. [Initialize fields of latest node and its link to the list]

INFO (NEW) ←X

If FIRST = NULL

Then LINK (NEW) ←NEW

FIRST ← LAST ←NEW

else LINK (NEW) ← FIRST

LINK (LAST)←NEW

FIRST ←NEW

Return

Q8 How polynomial is represented in a link list?

Linked list may be a arrangement that stores each element as an object during a node of the list. Every note contains two parts data han and links to subsequent node.

Polynomial may be a mathematical expression that consists of variables and coefficients. for instance x^2 - 4x + 7

In the Polynomial linked list, the coefficients and exponents of the polynomial are defined because the data node of the list.

For adding two polynomials that are stored as a linked list. We’d like to feature the coefficients of variables with an equivalent power. During a linked list node contains 3 members, coefficient value link to subsequent node.

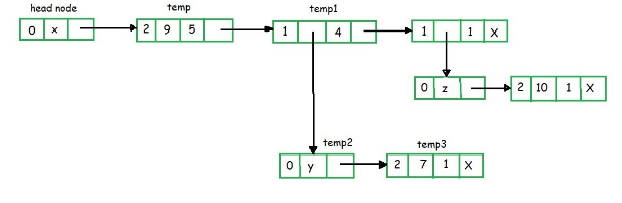
$C:\Users\Kilua Zoldyck\Pictures\gl2.png$

In the above example the top node is of variable x. The temp node shows the primary field as 2 means coefficient and exponent are present.

$C:\Users\Kilua Zoldyck\Pictures\gl3.png$

Since temp node is attached to go node and head node has variable x, temp node having coefficient = 9 and exponent = 5. The above two nodes are often read as 9x5.

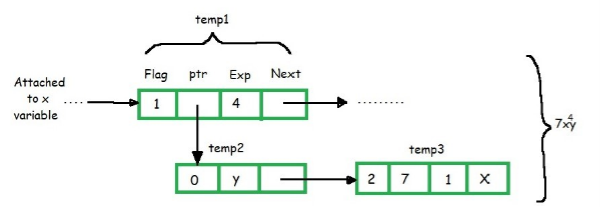
$C:\Users\Kilua Zoldyck\Pictures\gl4.png$

Similarly, within the above figure, the node temp1 are often read as x4.

The flag field is 1 means down pointer is there

temp2 = y

temp3 = coefficient = 7

exponent = 1

flag = 2 means the node contains coefficient and exponent values.

temp2 is attached to temp3 this suggests 7y1 and temp2 is additionally attached to

temp1 means temp1 x temp2

x4 x 7y1 = 7x4y1 value is represented by above figure

Q9 How items can be deleted in circular, singly and doubly link list?

Deletion a node from singly Linked List

If a linked list is empty, then write under flow and return.

Repeat step 3 while end of the list has not been reached and therefore the node has not been found.

Obtain subsequent node in list and record its predecessor node.

If the top of the list has been reached then write node not found and return.

Delete the node from list.

Return the node into availability area.

Function: DELETE(X, FIRST)

Given X, an address of node which we would like to delete and FIRST may be a pointer to the primary element of a linked linear list.

Typical node contains INFO and LINK fields. SAVE &PRED are temporary pointer variables.

8. [Is Empty list?]
If FIRST = NULL
then write (‘Underflow’)
return

9. [Initialize look for X]
FIRST←SAVE

10. [Find X]
Repeat thru step-5 while SAVE ≠ X and LINK (SAVE) ≠ NULL

11. [Update predecessor marker]
SAVE←PRED

12. [Move to next node]
LINK (SAVE)←SAVE

13. [End of the list]
If SAVE ≠ X
then write (‘Node not found’)
return

14. [Delete X]
If X = FIRST (if X is first node?)
LINK (FIRST)←then FIRST
LINK (X)←else LINK (PRED)

15. [Free Deleted Node]
Free (X)

Deletion in doubly link list

Function: DOUBDEL (L, R, OLD)

Given a doubly linked list with the addresses of left most and right most nodes are given by the pointer variables L and R respectively. It’s required to delete the node whose address is contained within the variable OLD. Node contains left and right links with names LPTR and RPTR respectively.

4. [Is underflow?]

If R=NULL

Then write (‘UNDERFLOW’)

return

5. 2. [Delete node]

If L = R (single node in list)

Then L ← R ← NULL

else If OLD = L (left most node)

Then L ←RPTR(L)

LPTR (L) ← NULL

else if OLD = R (right most)

Then R←LPTR (R)

RPTR (R) ← NULL

elseRPTR (LPTR (OLD)) ←RPTR (OLD)

LPTR (RPTR (OLD)) ←LPTR (OLD)

6. 3. [ FREE deleted node]

FREE (OLD

Deletion in circular link list

PROCEDURE: CIR_LINK_DELETE (X, FIRST, LAST)

9. [Is Empty List?]

If FIRST = NULL

Then write (‘Linked List is Empty’)

Return

10. [Initialize look for X]

SAVE ← FIRST

11. [Find X]

Repeat thru step 5 while SAVE ≠ X and SAVE ≠ LAST

12. [Update predecessor marker]

PRED← SAVE

13. [Move to next node]

SAVE ← LINK (SAVE)

14. [End of Linked List]

If SAVE ≠ X

Then write(‘Node not found’)

return

15. [Delete X]

If X = FIRST

Then FIRST ← LINK (FIRST)

LINK (LAST) ← FIRST

else LINK (PRED) ← LINK(X)

If X = LAST

Then LAST ←PRED

16. [Free Deleted Node]

Free (X)

Q10 How polynomial is added using a link list?

A linked list that's wont to store Polynomial seems like –

For all power, we'll check for the coefficients of the exponents that have an equivalent value of exponents and add them.

Then return the ultimate polynomial.

On addition on p1 and p2 we get resultant polynomial as P

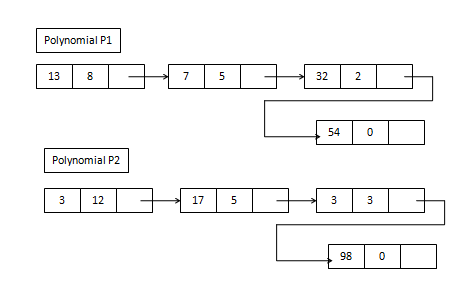
Input - Polynomial P1 and P2 represented as a linked list.

Polynomial

P1= 13x8 +7x5 + 32x2 +54

P2=3x12 +17x5 + 3x3 +98

Algorithm

Step 1: loop around all values of linked list and follow step 2& 3.

Step 2: if the value of a node’s exponent. Is greater copy this node to result node and head towards the next node.

Step 3: if the values of both node’s exponent is same add the coefficients and then copy the added value with node to the result.

Step 4: Print the resultant node.

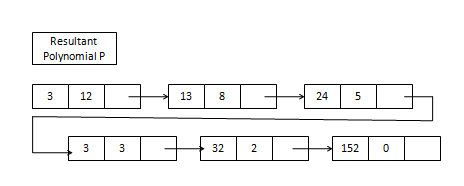
Resultant polynomial

P =3x12 +13x8 +24x5 +3x3 +32x2 +152

$C:\Users\Kilua Zoldyck\Pictures\po1.png$

Resultant polynomial after adding 2 polynomials p1 and p2

$C:\Users\Kilua Zoldyck\Pictures\pi.png$

Sign Up