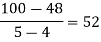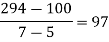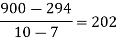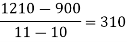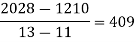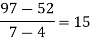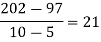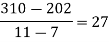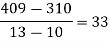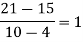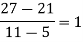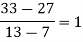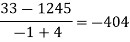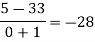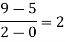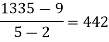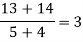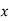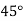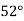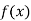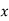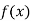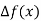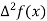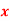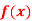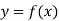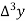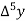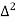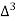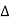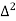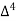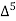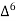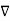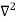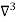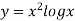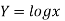Unit-6
Interpolation, Numerical integration, Solution of ordinary differential equations
Question-1: Using Newton’s divided difference formula, find the values of 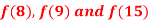 from the following table:
from the following table:
x | 4 | 5 | 7 | 10 | 11 | 13 |
f(x) | 48 | 100 | 294 | 900 | 1210 | 2028 |
We construct the divided difference table is given by:
x | f(x) | First-order divide difference | Second-order divide difference | Third-order divide difference | Fourth-order divide difference |
4
5
7
10
11
13 | 48
100
294
900
1210
2028 |
|
|
|
0
0 |
By Newton’s Divided difference formula
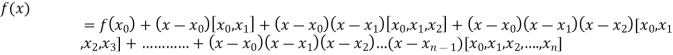 .
.
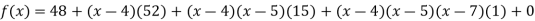
Now, putting 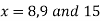 in above we get
in above we get
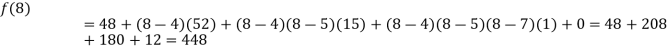 .
.
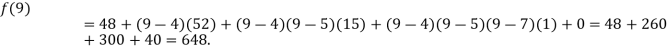
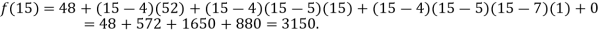
Question-2: Find a polynomial satisfied by 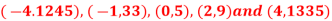 , by the use of Newton’s interpolation formula with a divided difference.
, by the use of Newton’s interpolation formula with a divided difference.
x | -4 | -1 | 0 | 2 | 4 |
F(x) | 1245 | 33 | 5 | 9 | 1335 |
Here
We will construct the divided difference table:
x | F(x) | First-order divided difference | Second-order divided difference | Third-order divided difference | Fourth-order divided difference |
-4
-1
0
2
4 | 1245
33
5
9
1335 |
|
|
|
|
By Newton’s divided difference formula
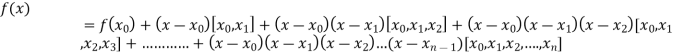 .
.

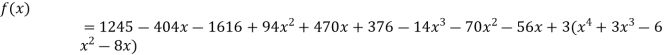
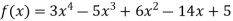
This is the required polynomial.
Question-3: Given  find
find  , by using Newton forward interpolation method.
, by using Newton forward interpolation method.
Let 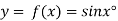 , then
, then
|
|
|
|
|
|
| 0.7071 | 0.7660 | - | 0.8192 | 0.8660 |
The table of forward finite difference is given below:
|
|
|
|
|
45
50
55
60 | 0.7071
0.7660
0.8192
0.8660 |
0.0589
0.0532
0.0468 |
-0.0057
-0.0064 |
-0.0007 |
By Newton forward difference method
Here initial value 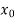 = 45, difference of interval h = 5 and the value to be calculated at x=52.
= 45, difference of interval h = 5 and the value to be calculated at x=52.
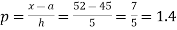
By Formula
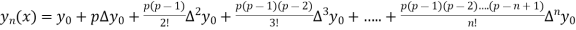

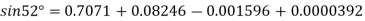
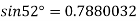
Question-4: Find 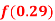 from the following table:
from the following table:
| 0.20 | 0.22 | 0.24 | 0.26 | 0.28 | 0.30 |
| 1.6596 | 1.6698 | 1.6804 | 1.6912 | 1.7024 | 1.7139 |
Consider the backward difference method
|
|
|
|
|
|
|
0.20
0.22
0.24
0.26
0.28
0.30 | 1.6596
1.6698
1.6804
1.6912
1.7024
1.7139 |
0.0102
0.0106
0.0108
0.0112
0.0115 |
0.0004
0.0002
0.0004
0.0003 |
-0.0002
0.0002
-0.0001 |
0.0004
-0.0003 |
-0.0007 |
Here 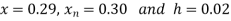
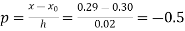
By Newton backward difference formula
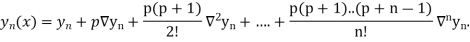
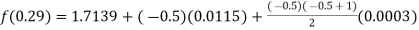
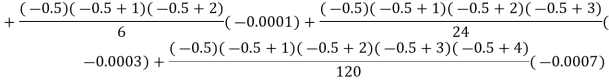
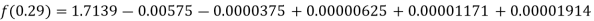
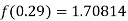
Question-5: The following are the marks obtained by492 candidate in a certain examination
Marks | 0-40 | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 |
No. of candidates | 210 | 43 | 54 | 74 | 32 | 79 |
Find out the number of candidates:
a) Who secured more than 48 but not more than 50 marks?
b) Who secured less than 48 but not less than 45 marks?
Consider the forward difference table given below:
Marks up to x | No. of candidates y |
|
|
|
|
|
40
45
50
55
60
65 | 210
210+43=253
253+54=307
307+74=381
381+32=413
413+79= 492 |
43
54
74
32
79 |
11
20
-42
47 |
9
-62
89 |
-71
151 |
222 |
Here 
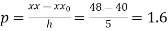
By Newton Forward Difference formula
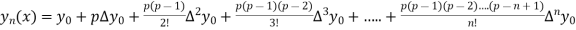
f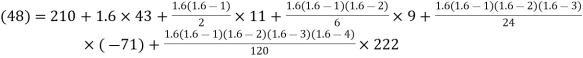
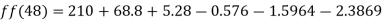

a) No. of candidate secured more than 48 but not more than 50 marks

b) No. of candidate secured less than 48 but not less than 45 marks
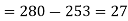
Question-6: Use the inverse Lagrange’s method to find the root of the equation 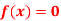 , give data
, give data 
X | 30 | 34 | 38 | 42 |
F(x) | -30 | -13 | 3 | 18 |
Here 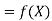 , we have the data
, we have the data

Also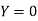 .
.
Lagrange’s inverse interpolation formula is given by

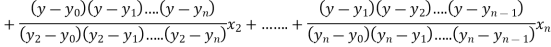
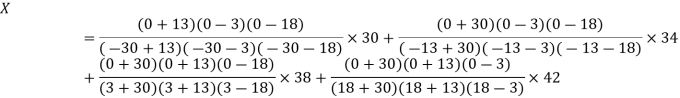

Thus the approximate root of the given equation is  .
.
Question-7: Given that
X | 1.0 | 1.1 | 1.2 | 1.3 |
Y | 0.841 | 0.891 | 0.932 | 0.963 |
Find 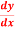 at
at 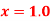 .
.
Here the first derivative is to be calculated at the beginning of the table, therefore forward difference formula will be used
Forward difference table is given below:
X | Y |
|
|
|
1.0
1.1
1.2
1.3 | 0.841
0.891
0.932
0.962 |
0.050
0.041
0.031 |
-0.009
-0.010 |
-0.001 |
By Newton’s forward differentiation formula for differentiation
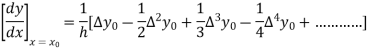
Here 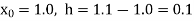
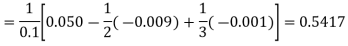
Question-8: From the following table of values of x and y find 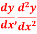 for
for 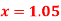
X | 1.00 | 1.05 | 1.10 | 1.15 | 1.20 | 1.25 | 1.30 |
Y | 1.0000 | 1.02470 | 1.04881 | 1.07238 | 1.09544 | 1.11803 | 1.14017 |
Here the value of the derivative is to be calculated at the beginning of the table.
Forward difference table is given by
X | Y |
|
|
|
|
|
|
1.00
1.05
1.10
1.15
1.20
1.25
1.30 | 1.0000
1.02470
1.04881
1.07238
1.09544
1.11803
1.14017 |
0.02470
0.02411
0.02357
0.02306
0.02259
0.02214 |
-0.00059
-0.00054
-0.00051
-0.00047
-0.00045 |
0.00005
0.00003
0.00004
0.00002 |
-0.00002
0.00001
-0.00002 |
0.00003
-0.00003 |
-0.00006 |
From Newton’s forward difference formula for differentiation we get
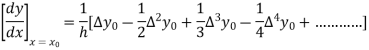
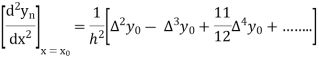
Here 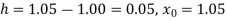
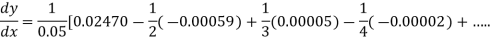
=0.48763
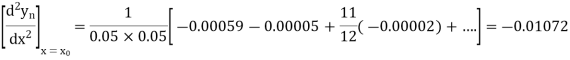
Question-9: Given that
X | 0.1 | 0.2 | 0.3 | 0..4 |
Y | 1.10517 | 1.22140 | 1.34986 | 1.49182 |
Find 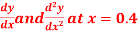 ?
?
Backward difference table:
X | Y |
|
|
|
0.1
0.2
0.3
0.4 | 1.10517
1.22140
1.34986
1.49182 |
0.11623
0.12846
0.14196 |
0.01223
0.01350 |
0.00127 |
Newton’s Backward formula for differentiation
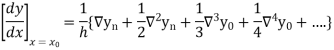
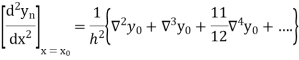
Here 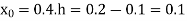
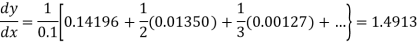
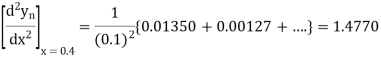
Question-10: Compute the value of 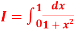 ?
?
Using the trapezoidal rule with h=0.5, 0.25, and 0.125.
Here 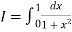
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule
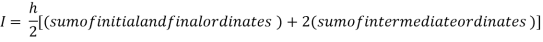
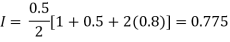
For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule
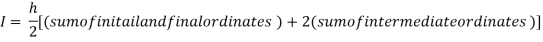
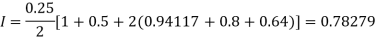
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule
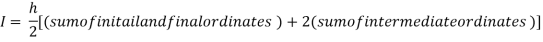
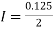 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
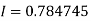
Question-11: Estimate the value of the integral
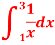
by Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 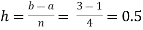
Construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
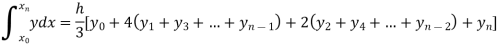
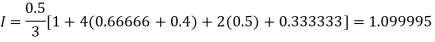
For n = 8, we have 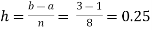
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule
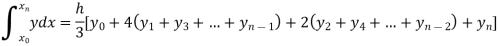

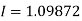
Question-12: Using Simpson’s 1/3 rule with h = 1, evaluate
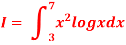
For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
| 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule
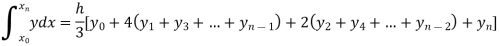
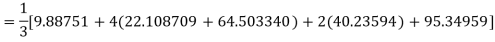
= 177.3853
Question-13: Evaluate 
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.
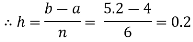
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5.0 | 5.2 |
| 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule


= 1.8278475
Question-14: Use Euler’s method to find y(0.4) from the differential equation
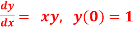 with h=0.1
with h=0.1
Given equation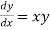
Here 
We break the interval into four steps.
So that 
By Euler’s formula
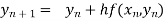 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
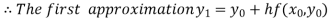
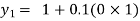
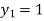
For n=1 in equation (i) we get
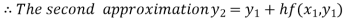
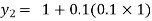
 .01
.01
For n=2 in equation (i) we get
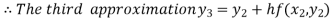

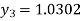
For n=3 in equation (i) we get

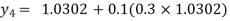
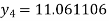
Hence y(0.4) =1.061106.
Question-15: Given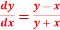 with the initial condition y=1 at x=0. Find y for x=0.1 by Euler’s method(five steps).
with the initial condition y=1 at x=0. Find y for x=0.1 by Euler’s method(five steps).
Given equation is 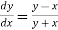
Here 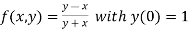
No. of steps n=5 and so that 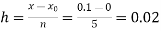
So that 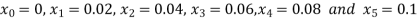
Also 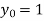
By Euler’s formula
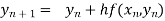 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
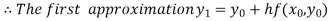
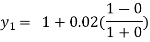
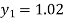
For n=1 in equation (i) we get
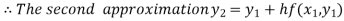
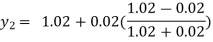
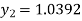
For n=2 in equation (i) we get

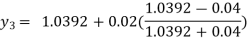
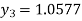
For n=3 in equation (i) we get
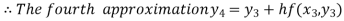
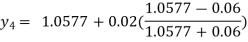

For n=4 in equation (i) we get
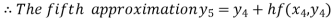
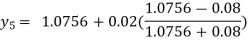
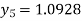
Hence 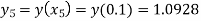
Question-16: Use modified Euler’s method to compute y for x=0.05. Given that

The result correct to three decimal places.
Given equation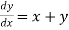
Here 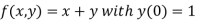
Take h = 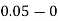 = 0.05
= 0.05
By modified Euler’s formula, the initial iteration is

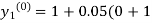 )
)

The iteration formula by modified Euler’s method is
 -----(i)
-----(i)
For n=0 in equation (i) we get
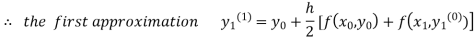
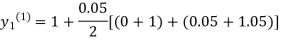
Where  and
and 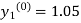 as above
as above
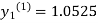
For n=1 in equation (i) we get
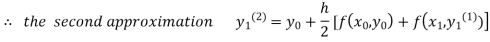

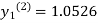
For n=3 in equation (i) we get
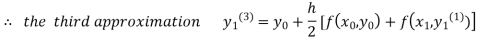
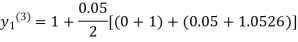
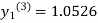
Since the third and fourth approximation is equal.
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Question-17: Use the Runge-Kutta method to find y when x=1.2 in the step of h=0.1 given that
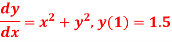
Given equation 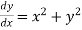
Here 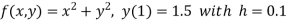
Also 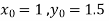
By Runge-Kutta formula for first interval
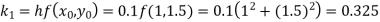
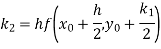
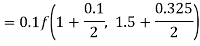
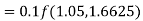
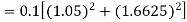
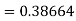
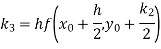
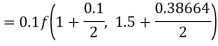
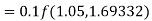
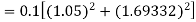
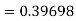
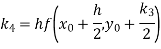
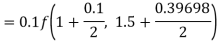
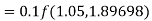
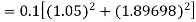
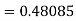
Again 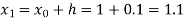
A fourth orderRunge-Kutta formula:
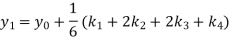


To find y at 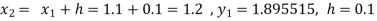
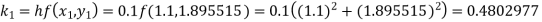
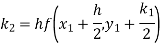
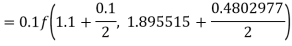
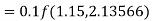
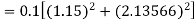
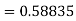
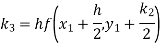
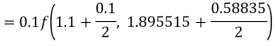
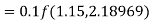

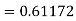
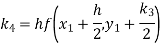
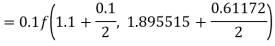
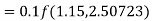
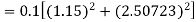
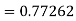
A fourth orderRunge-Kutta formula:
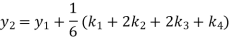

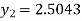
Question-18: Using the Runge-Kutta method of fourth-order, solve
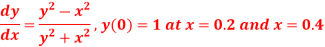
Given equation 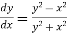
Here 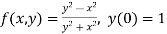
Also 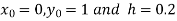
By Runge-Kutta formula for first interval
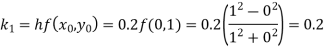
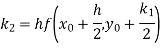
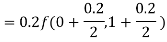

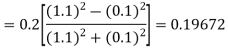
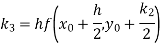
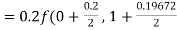 )
)

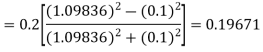
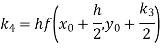
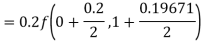
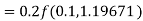
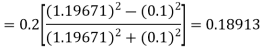
A fourth orderRunge-Kutta formula:
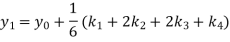
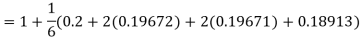
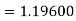
Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 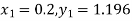
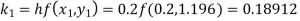
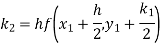
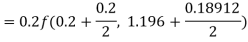
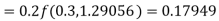

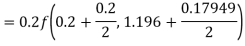

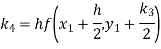
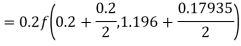
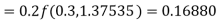
A fourth orderRunge-Kutta formula:

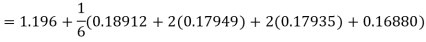

Hence at x = 0.4 then y=1.37527
Question-19: UsingRungeKutta method of order four, solve  to find
to find 
Given second order differential equation is
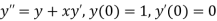
Let 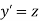 then above equation reduces to
then above equation reduces to
Or 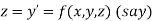
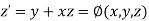 (say)
(say)
Or 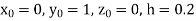 .
.
By RungeKutta Method we have
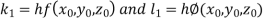
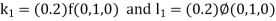

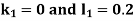
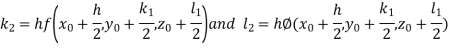
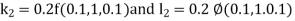
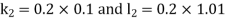

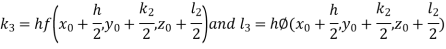
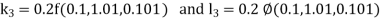

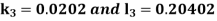
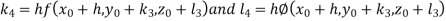
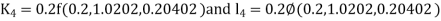
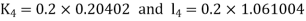

A fourth orderRungeKutta formula:
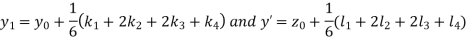
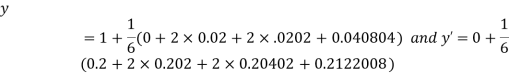

Question-20: Solve the differential equations
 for
for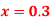
Using the four order RungeKutta method with initial conditions 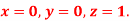
Given differential equation are
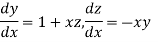
Let 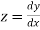
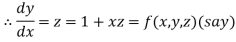
And 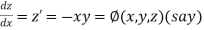
Also 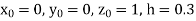
By RungeKutta Method we have
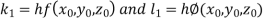
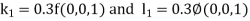
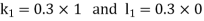
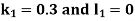
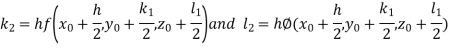
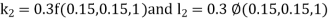
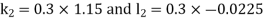

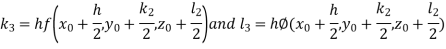
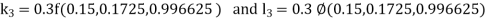
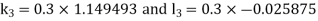
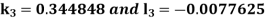
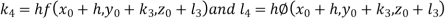
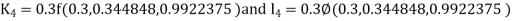
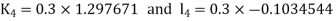

A fourth orderRungeKutta formula:
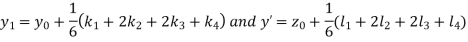
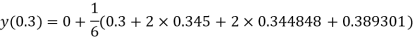
And 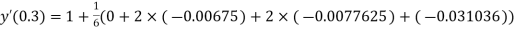
 .
.