Unit - 1

Digital Control System

Q1) List the advantages and limitations of digital control system.

A1) Advantages:

1. Power consumption is less in digital system as compared to analog system.
2. Digital systems can handle non-linear system easily which is the most important advantage of digital data in control system.
3. Digital systems work on the logical operations due to this they show decision making property which is very useful in the present world of machines.
4. They are more reliable as compared to analog systems.
5. Digital systems are easily available in compact size and have light weight.
6. They work on instructions we can program them as per our needs hence we can they are more versatile than analog systems.
7. Various complex tasks can be performed easily by the help of digital technology with a high degree of accuracy.

Limitations:

1. The mathematical analysis of a digital controller is sometimes more complex and more tedious as compared to continuous data control systems.
2. System stability is degraded by converting a continuous data system to digital system. Even a stable second order system can be unstable when converted to discrete version.
3. The signal output from the digital controller is to be converted to analog form before applying to the actuators. However, the reconstruction of digital to analog signal using hold circuits is only an approximation of the actual signal. So, some signal information is lost in the process.
4. Analog to Digital (A/D) and Digital to Analog (D/A) converters along with digital computer introduce some time delay.
5. The complexity of the controller is in the software implemented algorithms, which may contain errors

Q2) Explain Sampling in a signal.

A2) Sampling operation in sampled data and digital control system is used to model either the sample and hold operation or the fact that the signal is digitally coded. If the sampler is used to represent S/H (Sample and Hold) and A/D (Analog to Digital) operations, it may involve delays, finite sampling duration and quantization errors. On the other hand, used to represent digitally coded data the model will be much simpler. Following are two popular sampling operations:

1. Single rate or periodic sampling

2. Multi-rate sampling

Figure below shows the structure and operation of a finite pulse width sampler, where (a) represents the basic block diagram and (b) illustrates the function of the same. T is the sampling period and p is the sample duration.

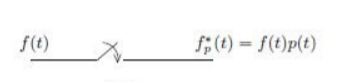
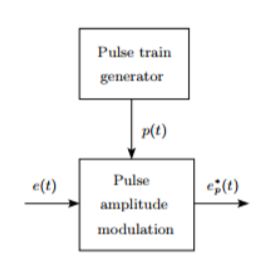
Figure (a): Basic block diagram

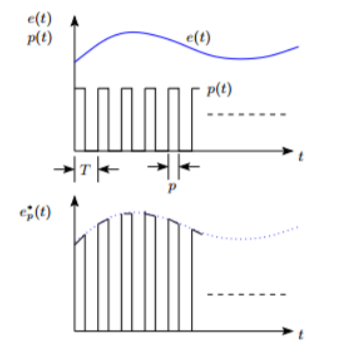
Figure (b): Sampler output

Finite pulse width sampler In general, a sampler is the one which converts a continuous time signal into a pulse modulated or discrete signal. The most common type of modulation in the sampling and hold operation is the pulse amplitude modulation.

The block diagram of sampler is shown above, having a pulse train of p seconds and sampling period of T seconds.

p(t)= unit pulse train with period T

p(t)=

Us(t)=unit step function

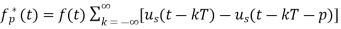
In frequency domain p(t) can be represented as

p(t)=

= 2π/T

Cn=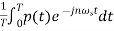

p(t)=1 for 0≤ t ≤p

The output of the ideal sampler can be expressed as

f*(t)=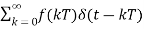

F*(s)=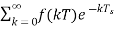

The output of a sampler is always followed by a hold device which is the reason behind the name sample and hold device. Now, the output of a hold device will be the same regardless the nature of the sampler and the attenuation factor p can be dropped in that case. Thus, the sampling process can be always approximated by an ideal sampler or impulse modulator.

Cn=

=

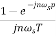
Q3) What is signal reconstruction?

A3) Reconstruction process

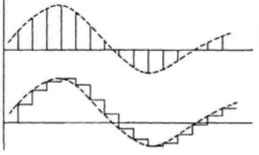
The digital data controller modifies the sampled data signal. This signal is than converted to analog form for the use in continuous parts of the system. This can be achieved by hold circuits. The simplest hold circuit is ZOH (zero order hold) in which the reconstructed signal acquires the same value as the last received sample for the entire sampling period.

Q4) Explain Shannon’s Sampling theorem.

A4) In sampling the signal m(t) is multiplied with periodic pulse train. Let M(ω) the spectrum of the input signal be band limited with the maximum frequency of fm as shown in figure 1.

Figure: 1

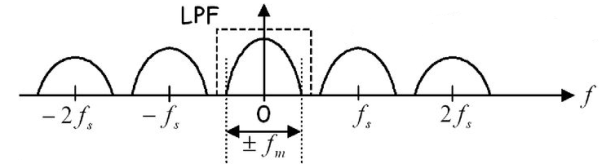
Figure: 2 (fs>2 fm)

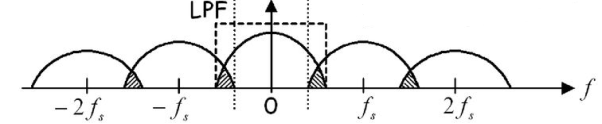
Figure: 3 (fs<2 fm)

The frequency spectrum of this signal when impulse sampled is plotted in figure 2 (for fs>2 fm). In figure 3 for (fs<2 fm). From figure 2 and figure 3 we can conclude that as long as fs≥2fm the original signal is preserved in the sampled signal and can be extracted from it by the low pass filter. This is known as Shannon’s Sampling theorem. This theorem states that the information contained in a signal is fully preserved in the sampled form as long as the sampling frequency is at lest twice the maximum frequency contained in the signal.

Q5) List the factors affecting the selection of sampling frequency.

A5)

1)     As seen above if fs>2 fm there are some problems. The frequency spectrum of the real signal does not possess fm. There are components outside the system bandwidth. So, there is loss of information as the frequency components outside the bandwidth will appear as the low frequency signals of frequencies between 0 and fs/2 due to aliasing effect.

2)     In control system the signal contains low frequency components containing useful information as well as high frequency noise components. The high frequency components appear as low frequency signals due to the aliasing effect causing the loss of information. To avoid aliasing analog filters are used before the sampler to reshape the   frequency spectrum of the signal. The cut off frequency fs/2 of the anti-aliasing filter should be higher than the system bandwidth otherwise the anti-aliasing filter becomes significant in determining the sampled response.

3)     Due to the conversion time and the computation time a digital algorithm contains a dead time. This dead time has a destabilizing effect on a closed loop system. So, the practical approach of selecting the sampling interval is to determine the stability limit of the closed loop control system as the sampling interval is increased.

4)     There are many digital control algorithms which are derived from analog algorithms by a process of discretization. In transformation of an algorithm from continuous time to discrete time errors arise. These errors become larger as the sampling interval increases.

5)     The Empirical rule for the selection of the sampling rate states that a sampling period needs to be selected much shorter than any of the time constants in the continuous time plant to be controlled digitally. The sampling rate equal to one tenth of the smallest time constant is recommended.

6)     The rule of thumb based on the closed loop performance is to select sampling interval T or less than one tenth of the desired settling time.

7)     The rule of thumb for open loop system plant model states that the selection of the sampling rate should be based on the closed loop performance of the control system. The selection of the sampling rate can be based on bandwidth of closed loop system. Usually sampling rate is 10-30 times the bandwidth.

Q6) Define ZOH and also derive its transfer function.

A6) Data hold is a process of generating a continuous-time signal h(t) from a discrete time signal x(kT). The signal x(kT) can be approximated by a polynomial 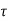as

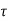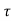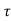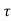h(kT+)=ann+an-1n-1+….+a1+a0                                                     0≤ ≤ T

h(kT)=x(kT)

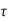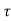h(kT+)=ann+an-1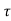n-1+….+a1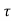+x(kT)

If the data hold circuit is an nth order polynomial it is called as nth order hold circuit.

Zero Order Hold (ZOH)

If n=0 in above equation the zero-order hold is obtained.

h(kT+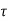)= x(kT)                                                         0≤ 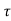≤ T    k=0,1,2,3…….

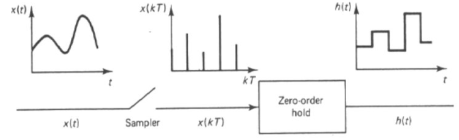
Fig: Zero Order Hold

h(t)=x(0)[u(t)-u(t-T)]+x(t)[u(t-T)-u(t-2T)]+x(2T)[u(t-2T)-u(t-3T)]……..

=

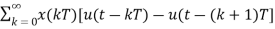
Taking Laplace transform of above equation we get

L[u(t-kT)] =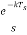

L[h(t)]=L{}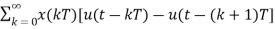

H(s)==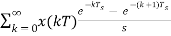

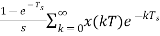
Gho(s)=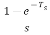

X*(s)=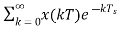

The transfer function of ZOH is Gho(s)=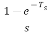

Q7) Derive the transfer function of first order hold.

A7) For first order hold system the equation will be

h(kT+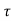)= a1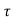+x(kT)                                                0≤ 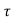≤ T    k=0,1,2,3……

h((k-1)T)=x((k-1)T)

h((k-1)T)=-a1T+x(kT)

Equating the above two equations we get

-a1T+x(kT)= x((k-1)T)

a1=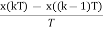

h(kT+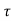)= a1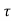+x(kT)

Substituting a1 in the above equation we get

h(kT+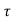)= x(kT) +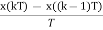 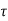                                0≤ ≤ T   

For obtaining the transfer function let the input to the system be a unit step function

x*(t)==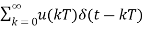

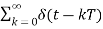
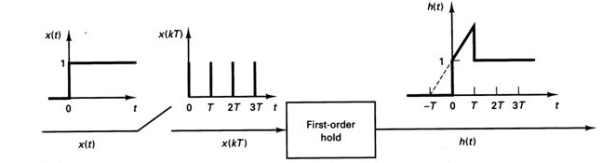
Fig: First Order Hold Circuit

h(t)=(1+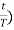u(t) - 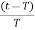u(t-T) – u(t-T)

Taking Laplace Transform of above equation we have

H(s)= (- -

= + 

=()

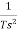
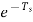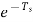
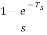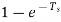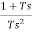
But we also know that L[u(t)]=

The transfer function for First Order Hold is given as

Gh1(s)=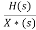 =()2( )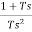

Gh1(s)= ( )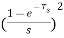

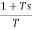Above equation is the required transfer function of First Order Hold.

Q8) Explain data conversion and quantization.

A8) The digitization of analog signals involves the rounding off of the values which are approximately equal to the analog values. The method of sampling chooses a few points on the analog signal and then these points are joined to round off the value to a near stabilized value. Such a process is called as Quantization.

The conversion of signals from analog into digital form and vice-versa is performed by A/D and D/A converters.

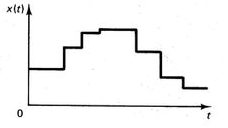
Fig: Original Signal                           Fig: Quantised Signal

Q9) Explain with the help of block diagram basic digital control system.

A9) A digital control system model can be viewed from different perspectives including control algorithm, computer program, conversion between analog and digital domains, system performance etc. One of the most important aspects is the sampling process level. In continuous time control systems, all the system variables are continuous signals. Whether the system is linear or nonlinear, all variables are continuously present and therefore known (available) at all times.

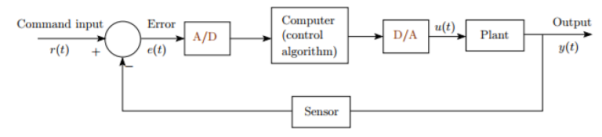
Figure: Sampled Data control system

In a digital control system, the control algorithm is implemented in a digital computer. The error signal is discretized and fed to the computer by using an A/D (analog to digital) converter. The controller output is again a discrete signal which is applied to the plant after using a D/A (digital to analog) converter. General block diagram of a digital control system is shown in Figure above. e(t) is sampled at intervals of T. In the context of control and communication, sampling is a process by which a continuous time signal is converted into a sequence of numbers at discrete time intervals. It is a fundamental property of digital control systems because of the discrete nature of operation of digital computer.