Unit - 2
Z-transform and Pulse-transfer-function
Q1) Define initial and final value theorem.
A1) Initial value and final value theorems of z-transform are defined for causal signal.
Initial Value Theorem
For a causal signal x(n), the initial value theorem states that
x(0) = ltz→∞X(z)
This is used to find the initial value of the signal without taking inverse z-transform
Final Value Theorem
For a causal signal x(n), the final value theorem states that
x(∞) = ltz→1[z−1]X(z)
This is used to find the final value of the signal without taking inverse z-transform.
Q2) Find the inverse z-transform of X(z)= 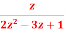 , |z|<
, |z|< .
.
A2) Finding inverse z-transform by power series method
X(z)= 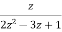 ROC :|z|<
ROC :|z|<
From the given ROC it is clear that the sequence is left sided. Hence, the power of z should be positive.
1-3z+2z2) z (z+3z2+7z3+15z4
- z-3z2+2z3
-----------------
3z2-2z3
- 3z2-9z3+6z4
-----------------
7z3-6z4
- 7z3-21z4+14z5
-------------------
15z4-14z5
- 15z4-45z5+30z6
-------------------
31z5-30z6
=z+3z2+7z3+15z4+31z5+…………
=…………+15z4+7z3+3z2+z
=………….+15z-(-4)+7z-(-3)+3z-(-2)+z
 X[n]={…….15,7,3,1,0}
X[n]={…….15,7,3,1,0}
Q3) Find the inverse z-transform of X(z)= 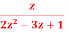 , |z|>1.
, |z|>1.
A3) 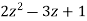 ) z (
) z ( +
+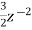 +
+ +
+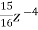
z- +
+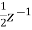
--------------
 -
-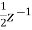
 -
-  +
+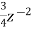
------------------
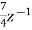 -
-
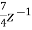 -
- 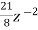 +
+ 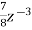
--------------------------
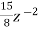 -
-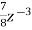
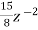 -
-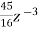 +
+ 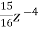
-------------------------------
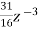 -
-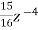
X(z)= 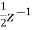 +
+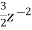 +
+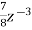 +
+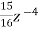 +……….
+……….
x(n) = {0,  ,
, 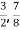 ,
,  …………}
…………}
Q4) Find the inverse z-transform of X(z)= 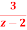 . Using partial fraction method. ROC |z|>2?
. Using partial fraction method. ROC |z|>2?
A4) X(z)=
Dividing both sides by z
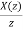 =
=
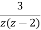 =
= +
+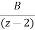
3=A(z-2)+Bz
Equating coefficients of z and z0 on both sides we get
A+B=0
-2A+B=3
Solving above two equations and we get A=-3/2 and B=3/2
 =
=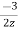 +
+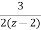
X(z)= +
+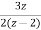
Taking inverse of above equation
X[n]=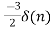 +
+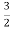 (2)nu(n)
(2)nu(n)
Q5) Solve the second order difference equation 2x(n-2)-2x(n-1)+x(n)=3n-2 n>0, where x(-2)=-4/9 and x(-1)=-1/3?
A5) Taking Z-transform of both sides
Z[ 2x(n-2)-2x(n-1)+x(n)]=Z[3n-2 ]
Using the above equation of generalised form we get
2[z-2X(z)+z-1x(-1)+x(-2)]-3[z-1X(z)+x(-1)]+X(z)=3-2. 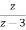
Already given x(-2)=-4/9 and x(-1)=-1/3
Finally, substituting the values and solving above equation we get
X(z)=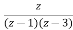
X(z)/z=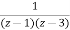
Now by partial fraction method we get
 =
= +
+ 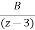
z=A(z-3)+B(z-1)
A+B=1
-3A-B=0
Solving above equations and finding A and B
A=-1/2 B=3/2
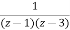 =
=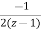 +
+ 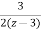
X(z)=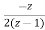 +
+ 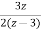
X(z)= [
[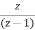 +
+ 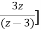
Taking inverse transform of above equation, we get (refer table of z-transform)
x[n]=  [3n-1] n>0
[3n-1] n>0
Q6) Find pulse transfer function of ZOH.
A6) Consider a system with hold circuit and closed loop system shown below.

Fig: Closed loop system with hold circuit
The relation between input and output can be given as
E(s)=R(s)-G(s) H(s) E*(s)
C(s)=G(s)E*(s)
The pulse transform will then be
E*(s)=R*(s)-G*(s)H*(s)E*(s)
E*(s)=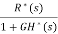
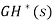 =[G(s)H(s)]*
=[G(s)H(s)]*
C(s)=G(s) E*(s)
=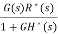
Taking pulse transform of above equation we get
C*(s)=[G(S)E*(s)]*
= =
=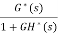
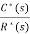 =
=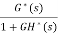
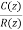 =
=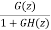
GH(z)=Z[G(s)H(S)]
The z-transfer function is  =
=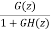
The pulse transfer function is 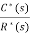 =
=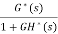
Q7) Find z-transform of x(n) = anu(n) a<1.
A7) X(z) =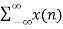 z-n
z-n
=  z-n
z-n
= 1+ +………
+………
The above series is GP of infinite terms so
X(z)= 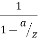 =
= 
Q8) Find z-transform of x(n) = 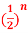 u(n).
u(n).
A8) X(z) =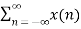 z-n
z-n
= z-n
z-n
= 1+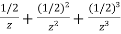 +……
+……
The above series is GP of infinite terms so
X(z)= 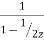 =
= 
Q9) Find z-transform and ROC for x(n) =  u(n) +
u(n) + u(-n-1).
u(-n-1).
A9) Let x1(z)= 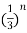 u(n) |z|>1/3
u(n) |z|>1/3
The z-transform of x1(z) will be x1(n)= 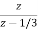
x2(z)= 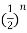 u(-n-1)
u(-n-1)
X(z) = z-n
z-n
Limits will change from n= -1 to 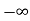
X2(z) = z-n
z-n
= (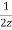 )-1+ (
)-1+ (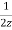 )-2+(
)-2+( )-3+….
)-3+….
=2z+(2z)2+(2z)3+ ……..
x2(n)= 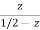 ½>|z|
½>|z|
The ROC will lie be 1/3<|Z|<1/2
Q10) Find IZT of X(z) = 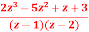 |z|>1.
|z|>1.
A10) X(z) = 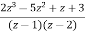
z2-3z+2 ) 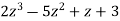 ( 2z+1
( 2z+1
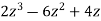
----------------------
z2-3z+3
z2-3z+3
--------------
1
By partial fraction method
X(z)= 2z+1 + 
=2z+1 + 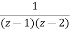
Solving the above we finally get
X(z) = (2z+1) +  -
-  +
+ 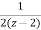
Now let X1(z) = 2z+1
Taking inverse of above we get x1(n) = 2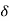 (n+1) +
(n+1) +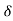 (n)
(n)
Let X2(z)= 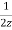 -
-  +
+ 
Taking inverse z transform of above we get
x2(n) = 
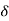 (n) – (1)n u(n) +
(n) – (1)n u(n) +  (2)n u(n) [refer table in notes]
(2)n u(n) [refer table in notes]
x(n)= x1(n) + x2(n)
= 2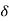 (n+1) +
(n+1) +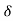 (n) +
(n) + 
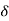 (n) – (1)n u(n) +
(n) – (1)n u(n) +  (2)n u(n)
(2)n u(n)
= 2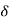 (n+1) +
(n+1) + 
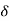 (n) + [2n-1 – 1] u(n)
(n) + [2n-1 – 1] u(n)