Unit - 3
Stability Analysis
Q1) G(s)=2/s(s+2). Find the characteristic equation for the transfer function H(z) with unity feedback. Let T=0.2sec?
A1) Sol: G(s)=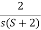
Finding G(z)= z[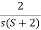
]
=
=
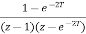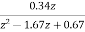(T=0.2sec)
Hence, the characteristic equation will be
1+G(z)H(z)=0
But there is unity feedback so
1+G(z)=0
1+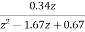
=0
z2-1.34z+0.67=0
The required characteristic equation is z2-1.34z+0.67=0
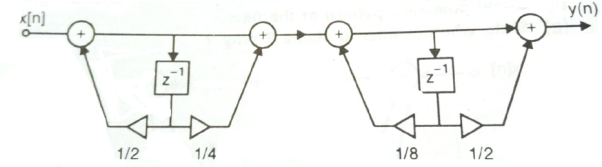
Q2) For the following LTI system H(z)=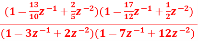 
. Realise the cascade form IIR filter.
A2) Sol: H(z)=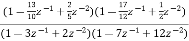
The above function can be simplified as
H(z)=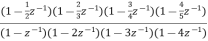
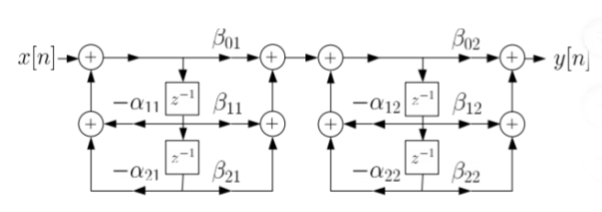
Hence, using the above structure and placing the values of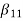 
…. And similarly, 
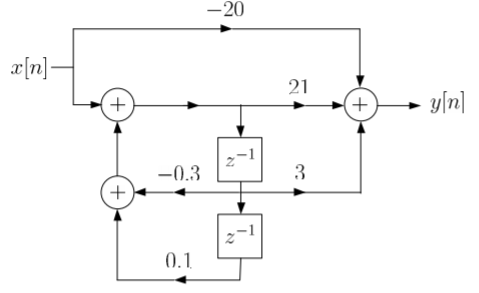
Q3) Draw block diagram for the function using parallel form H(z)=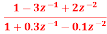
.
A3) H(z)=
Writing above transfer function in standard form for parallel realisation we get
H(z)=-20+
The structure is shown below
Q4) Using bilinear transformation, determine the characteristic equation of given open loop function in z-plane. G(s)= 
.
A4) Sol: G(s)=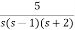
=5[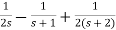 
]
=5[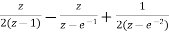 
]
=
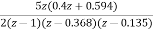
The characteristic equation is given as
1+G(S)=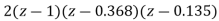
+
=0
z3-0.5z2+2.49z-0.496=0
Putting in equation below
The characteristic equation is
an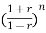
+ an-1 
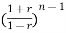+………..+a1
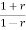+a0=0
-0.5
+2.49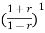
-0.496=0
The system stability can be checked using Routh array
The characteristic equation in s-domain will be
1+G(s)=0
1+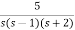
=0
s3+3s2+2s+5=0
s3 1 2
s2 3 5
s1 1/3 0
s0 5 0
First column no sign change. Hence, system is stable.
Q5) Consider the characteristic equation of the second-order system F1(z)=a2z2+a1z+a0=0 for a2>0. The stability constrains will be?
A5) F1(z=1)=a2+a1+a0 >0
(-1)n F1(z=-1)= a2-a1+a0 >0
|
|< 
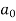Q6) For the system given y(n) -
y(n-1) + 
y(n-2) = x(n) + 
x(n-1) realize using cascade form?
A6) The system transfer function is given as
H(z) = Y(z)/X(z)
Taking z transform of y(n) -
y(n-1) + 
y(n-2) = x(n) + 
x(n-1)
Y(z) - 
z-1Y(z) + 
z-2 Y(z) = X(z) + 
z-1 X(z)
H(z)=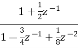 
Again, simplifying the above function to get into standard cascade form we ca write
H(z) = 
= H1(z)+H2(z)
H1(z)=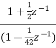 
H2(z)=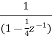 
The final structure is shown below
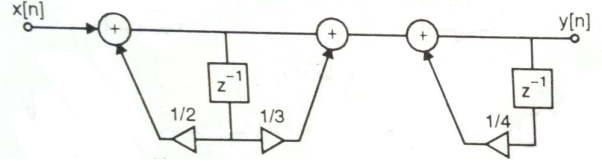
Q7) For the following LTI system H(z)=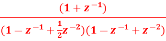 
. Realise the cascade form?
A7) H(z)=
Writing the above in standard form for cascade realisation
H1(z)= 
H2(z)= 
The cascade structure is shown below
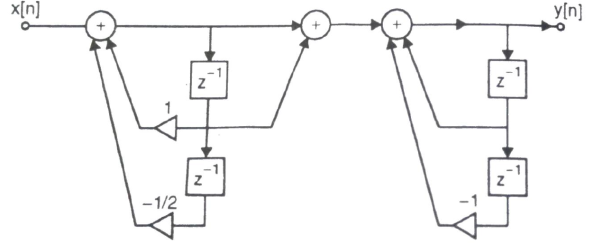
Q8) Realize the system transfer function using parallel structure H(z)=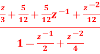 
.
A8) H(z)=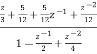 
Taking Z common and then dividing the above function to convert it into standard form for parallel realisation we get
H(z)=Z [ 
+
+
]
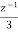The parallel structure is shown below
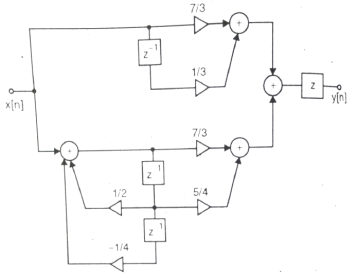
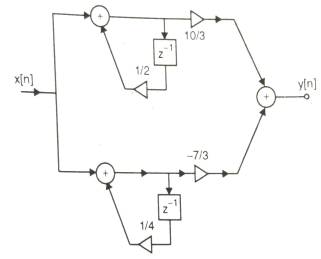
Q9) Realize the system transfer function using parallel structure H(z)=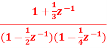 
.
A9) Converting the above function to standard form using partial fraction technique
H(z)=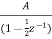 
+ 
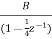
Solving for A and B we get
A= 10/3
B= -7/3
H(z) =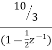 
+ 
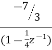
H1(z) =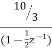 
H2(z) = 
The parallel form realisation is shown below
Q10) For the transfer function H(z) = 
. Realise using cascade form?
A10) H(z) =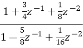 
Writing in standard form
H(z) = 
H1(z) =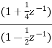 
H2(z) =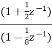 
The cascade structure is shown below
