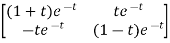Unit 5
Solution of State Equations
Q1) Obtain the eigenvectors of matrix A = 
A1) For eigenvalues |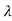 iI-A|=0
iI-A|=0
|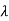 I-A|=
I-A|=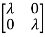 -
- 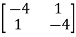 =0
=0
| I-A| =
I-A| = 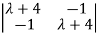 =0
=0
|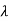 I-A| = (
I-A| = (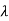 +4)2-1=0
+4)2-1=0
| I-A| =
I-A| = 2+8
2+8 +15=0
+15=0
The eigen values are
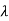 1=-3,
1=-3, 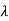 2=-5
2=-5
Q2) Obtain the eigenvalues of system described as 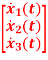 =
= +
+  [u] and y= [1 0 0]
[u] and y= [1 0 0]
A2) For eigenvalues |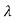 iI-A|=0
iI-A|=0
| I-A|=
I-A|=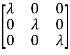 -
- 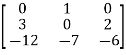 =0
=0
| I-A| =
I-A| = 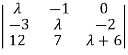 =0
=0
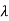 3+6
3+6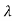 2+11
2+11 +6=0
+6=0
(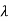 +1) (
+1) ( +2) (
+2) ( +3) = 0
+3) = 0
Hence eigen values are 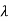 1=-1,
1=-1, 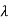 2=-2,
2=-2, 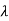 3= -3
3= -3
Q3) Find eigen vectors for the following system  =
=  +
+ [u] and y= [1 0 0]
[u] and y= [1 0 0] .
.
A3) Refer above que 2. The eigen values are 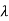 1=-1,
1=-1, 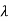 2=-2,
2=-2, 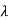 3= -3
3= -3
The eigen vectors will be
For 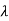 1=-1
1=-1
|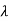 I-A|X = 0
I-A|X = 0
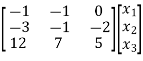 = 0
= 0
-x1-x2 = 0
3x1 + x2 + 2x3 = 0
12x1+7x2+5x3=0
Solving above equations we get x1 = 1, x2= -1 as x3 = -1
Therefore, the eigen vectors are 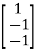
For 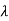 2=-2
2=-2
|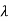 I-A|X = 0
I-A|X = 0
 = 0
= 0
-2x1-x2 = 0
3x1 + 2x2 + 3x3 = 0
17x1+7x2+4x3=0
Solving above equations we get x1 = 2, x2= -4 as x3 = -1
Therefore, the eigen vectors are 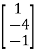
For 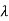 3=-3
3=-3
|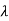 I-A|X = 0
I-A|X = 0
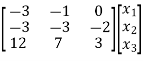 = 0
= 0
3x1+x2 = 0
3x1 + 3x2 + 2x3 = 0
12x1+7x2+3x3=0
Solving above equations we get x1 = 1, x2= -3 as x3 = 3
Therefore, the eigen vectors are 
Q4) Find the eigenvectors of the matrix A=  .
.
A4) For eigenvalues | iI-A|=0
iI-A|=0
|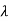 I-A|=
I-A|=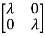 -
- 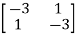 =0
=0
| I-A| =
I-A| = 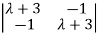 =0
=0
|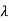 I-A| = (
I-A| = ( +3)2-1=0
+3)2-1=0
|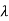 I-A| =
I-A| =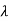 2+6
2+6 +8=0
+8=0
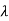 1=-2,
1=-2, 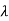 2=-4
2=-4
For  1=-2 the eigenvectors are
1=-2 the eigenvectors are
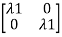 -
- 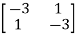 x Xi=0
x Xi=0
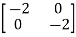 -
- 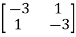 x
x  = 0
= 0
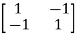
 = 0
= 0
-x1+x2=0
For x1=1 x2=1 the equation above is satisfied.
Xi=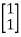
For 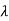 2=-4
2=-4
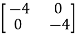 -
- 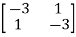 x
x  = 0
= 0
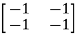
 = 0
= 0
-x1-x2=0
For x1=1 x2= -1 the equation above is satisfied.
Xi=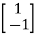
Q5) For the given matrix A=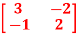
A5) For eigen values
|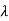 I-A|=
I-A|=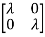 -
- 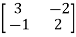 =0
=0
| I-A| =
I-A| = 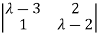 =0
=0
|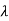 I-A| = (
I-A| = (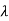 -3)(
-3)(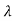 -2)-2=0
-2)-2=0
|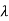 I-A| =
I-A| =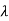 2-5
2-5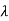 +4=0
+4=0
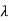 1=1,
1=1, 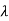 2=4
2=4
For 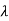 1=1 the eigenvectors are
1=1 the eigenvectors are
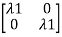 -
- 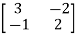 x Xi=0
x Xi=0
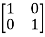 -
- 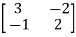 x
x  = 0
= 0
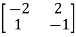
 = 0
= 0
-2x1+2x2=0
For x1=1 x2=1 the equation above is satisfied.
X1=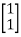
For 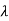 2=4
2=4
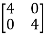 -
-  x
x  = 0
= 0
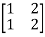
 = 0
= 0
x1+2x2=0
For x1=2 x2= -1 the equation above is satisfied.
X2=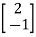
Arrange eigenvectors in a matrix P = 
P-1= - 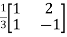 =
=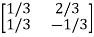
The transformation matrix 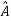 =P-1AP
=P-1AP
=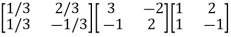
=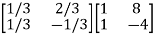
=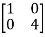
Q6) A system is represented by the state equation and output equation as
 =
= 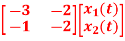 +
+ u(t) and Y=[1 2]
u(t) and Y=[1 2]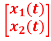
Find the poles of the system and comment on stability.
A6) A= 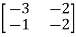
The characteristic equation is given as
|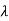 I-A|=
I-A|=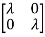 -
-  =0
=0
|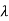 I-A| =
I-A| = 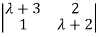 =0
=0
| I-A| = (
I-A| = ( +3) (
+3) (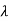 +2)-2=0
+2)-2=0
|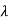 I-A| =
I-A| =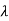 2+5
2+5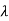 +4=0
+4=0
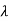 1=-1,
1=-1, 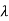 2=-4
2=-4
The poles are -1 and -4. Both on left half of s-plane so system is stable.
Q7) The state and output equation of LTI system is  =
=  +
+ [u] and y= [1 1 0]
[u] and y= [1 1 0] . Find the characteristic equation.
. Find the characteristic equation.
A7) The characteristic equation is given as | I-A|=0
I-A|=0
| I-A|=
I-A|= -
-  =0
=0
|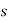 I-A| =
I-A| = 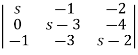 =0
=0
The characteristic equation is
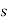 3-5
3-5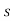 2-8
2-8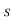 +2=0
+2=0
Hence poles are  1=-1,
1=-1,  2=-2,
2=-2, 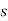 3= -3
3= -3
Q8) For matrix A= 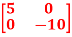 . Find the state transition matrix.
. Find the state transition matrix.
A8) The state transition matrix is given by L-1[SI-A]-1=φ(t)
[SI-A]=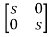
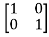 -
-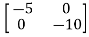
=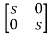 -
-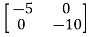
=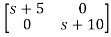
Taking inverse Laplace of above, we get
[SI-A]-1=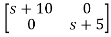 /(S+5)(S+10)
/(S+5)(S+10)
=
Hence φ(t)=L-1[SI-A]-1=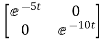
Q9) Find state transition matrix if A =  .
.
A9) The state transition matrix is given by L-1[SI-A]-1=φ(t)
[SI-A]=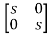 -
-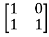
=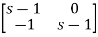
[SI-A]-1=
Hence φ(t)=L-1[SI-A]-1=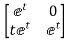
Q10) A=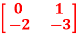 . Calculate characteristic equation and stability.
. Calculate characteristic equation and stability.
A10) The characteristic equation is given as [SI-A]=0
S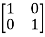 -
- 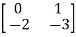 =0
=0
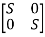 -
-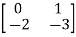 = 0
= 0
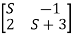 =0
=0
S(S+3)-(-1)*2=0
Hence, the characteristic equation is
S2+3S+2=0
(S+1)(S+2)=0
S=-1,-2
Both roots on left-half of s-plane, real and different, system absolutely stable.
Q11) A= 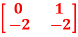 . Find the characteristic equation and comment on stability.
. Find the characteristic equation and comment on stability.
A11) The characteristic equation is given by [SI-A] =0
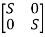 -
-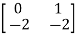 =0
=0
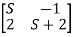 =0
=0
S(S+2)+2=0
S2+2S+2=0
S=-1±j
Roots on left-half of s-plane, complex conjugate, system absolutely stable.
Q12) Find f(A)=eAt for A=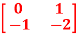 .
.
A12) The characteristic equation is
q( )=|
)=|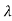 I-A|=
I-A|= =(
=(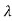 +1)2=0
+1)2=0
The eigen values of A are 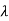 1,
1, 2=-1
2=-1
Since, A is of second order, R(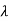 ) will be
) will be
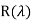 =
= 0+
0+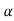 1
1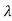
Then 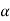 0 and
0 and 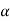 1
1
f(A)= 0+
0+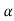 1
1
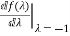 =te-t
=te-t
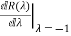 =
=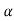 1
1
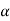 0=(1+t)e-t
0=(1+t)e-t
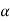 1=te-t
1=te-t
f(A)=eAt=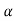 0I+
0I+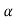 1
1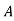
=